In IPCC AR5, capitolo 8 SM (Supplementary Material) “Anthropogenic and Natural Radiative Forcing”, a pagina 8SM-7 viene presentata, tra le altre, la formula del forcing radiativo ΔF (indicato anche come RF, in W/m2) per la CO2
| ΔF=5.35 x ln(C/Co) | (1) |
|---|
con C concentrazione attuale di CO2, in ppm, e Co concentrazione di riferimento (qui si usa quella pre-industriale del 1760, pari a 280 ppm).
Seim e Olsen (2020), nella descrizione di un interessante esperimento per verificare sperimentalmente il riscaldamento aggiuntivo dell’atmosfera ad opera dei gas serra, riportano altre formule collegate alla (1)
| ΔT=λ ΔF | (2) |
|---|
dove ΔF è l’aumento della radiazione (in W/m2) diffusa all’indietro dalla CO2 (effetto serra). La costante λ, viene detto, vale circa 0.8.
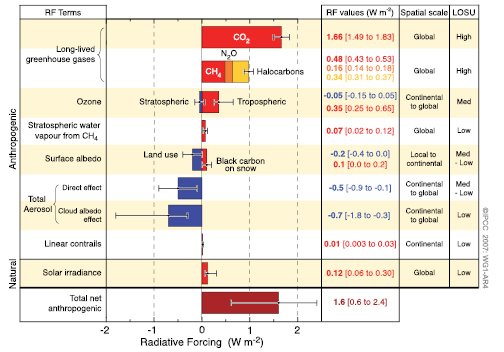
Ancora in AR5 si stima che un raddoppio della CO2 in aria comporti un forcing infrarosso (IR) di 3.7 W/m2 e un aumento di temperatura di circa 3°C. Infatti:
| ΔF= 5.35 x ln(2) = 3.708 W/m2 |
|---|
e
| ΔT= 0.8 x 3.708 = 2.967 °C |
|---|
Dalla sostituzione della (1) nella (2) si ottiene
| ΔT= λ x 5.35 x ln(C/Co) | (3) |
|---|
ovvero:
| ΔT= slope x ln(C/Co) | (3a) |
|---|
cioè una relazione lineare tra variazione di temperatura ΔT e logaritmo naturale del rapporto tra le concentrazioni della CO2 attuale e quella di riferimento.
Questa relazione è alla base delle affermazioni che stabiliscono la necessità di evitare le emissioni di CO2 in atmosfera per limitare l’aumento di temperatura del pianeta.
Mi propongo qui di verificare la relazione (3a) su estensioni temporali diverse (anche molto grandi), utilizzando anche i dati di prossimità sia per la temperatura (δ18O) che per l’anidride carbonica (carote antartiche). Il confronto viene realizzato su quattro intervalli temporali:
- 1981-2012, tra l’anomalia di temperatura globale terra+oceano di GHCN (NOAA) di gennaio 2021 (file 2101t.dat) e la CO2 di Mauna Loa (Hawaii), entrambi a passo mensile (file diff12-co2.dat). L’estensione è di 32 anni.
- 1976-2019, tra la stessa serie di temperatura (2101t.dat) e la CO2 di Mauna Loa (mlo69-19.txt). L’estensione è di 44 anni.
- 50-0 Ka, tra i dati mostrati in precedenza su http://www.climatemonitor.it/?p=52003, lo18o_td.txt e antarctica2015co2composite.txt della stazione antartica russa, Vostok. L’estensione è pari a 50 mila anni. Le due serie hanno passo diverso, il che rende complicato il confronto, per cui entrambe sono state digitalizzate ad un passo costante di 20 pixel, pari a 1052 anni (~1 kyr), per ottenere i due file effettivamente usati nel confronto, co2-dig.txt e d18o-dig.txt. Queste serie sono indicate come “Vostok”.
- 424-3 Ma, tra CO2 e δ18O digitalizzate dalla figura di Davis (2017). L’estensione temporale è di 421 milioni di anni. Nel seguito queste serie sono indicate con “Davis”.
Nel caso di “Vostok” il ΔT dell’equazione (3a) viene calcolato come singolo valore di d18O meno la media dell’intera serie, cioè è lo scarto dalla media.
Nel caso di “Davis” il ΔT è il detrended di d18O, ovvero lo scarto dal fit lineare della serie.
In tutti i casi, come valore di riferimento per la concentrazione di CO2 viene usato 280 ppm.
Nel sito di supporto sono disponibili i grafici delle singole equazioni (3a) mentre qui mostro le quattro relazioni raggruppate.
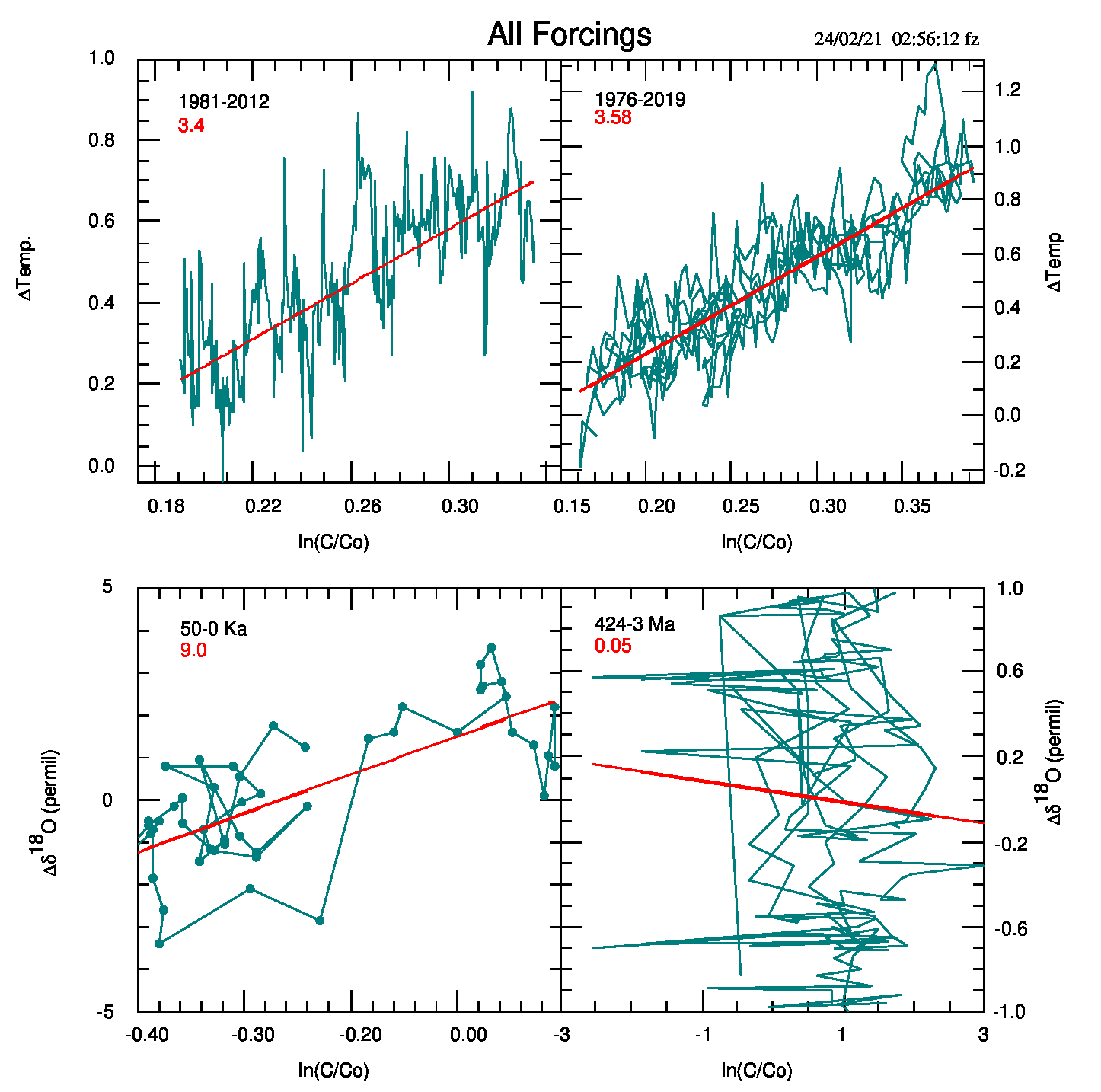
Dalle equazioni (3) e (3a) segue che la costante λ può essere calcolata a posteriori come λ=slope/5.35 e i valori della pendenza riportati in rosso nella figura 1 permettono di verificare che λ per i quattro casi vale 0.63 e 0.67 (°C m2/W); 1.68 e 0.009 (permille m2/W).
La relazione (3a) si verifica, come andamento medio, per tre delle quattro estensioni temporali ma, a parte il primo caso di 32 anni, la relazione media viene generata attraverso una complicata serie di avanzamenti e arretramenti (ghirigori o disegni casuali) che non fanno pensare ad un rapporto diretto tra aumento della concentrazione di CO2 e temperatura. La natura delle serie, specialmente le più estese, può generare (e ha generato) dubbi sull’effettivo allineamento temporale delle due variabili: voglio sottolineare che è stata posta un’attenzione particolare nel verificare questo allineamento.
A titolo di curiosità (ma non troppo) propongo, in tabella 1, una selezione di corrispondenze tra i massimi e i minimi dei due quadri superiori di figura 1 e gli eventi (El Nino, La Nina):
| ln(C/Co) | CO2 | Evento | Carattere |
|---|---|---|---|
| 1981-2012 | |||
| 0.196 | 340.6 | 1982, El Nino | molto forte |
| 0.223 | 349.9 | 1987-88, El Nino | forte |
| 0.246 | 358.1 | 1995-96, La Nina | debole |
| 0.262 | 363.9 | 1997-98, El Nino | molto forte |
| 0.315 | 383.7 | 2007, La Nina | moderato |
| 0.325 | 387.5 | 2010, El Nino | molto forte |
| 1976-2019 | |||
| 0.180 | 335.2 | 1977-78, El Nino | debole |
| 0.205 | 343.7 | 1982-83, El Nino | molto forte |
| 0.270 | 366.8 | 1997-98, El Nino | molto forte |
| 0.320 | 385.6 | 2007-08, La Nina | moderato |
| 0.370 | 405.4 | 2016, El Nino | forte |
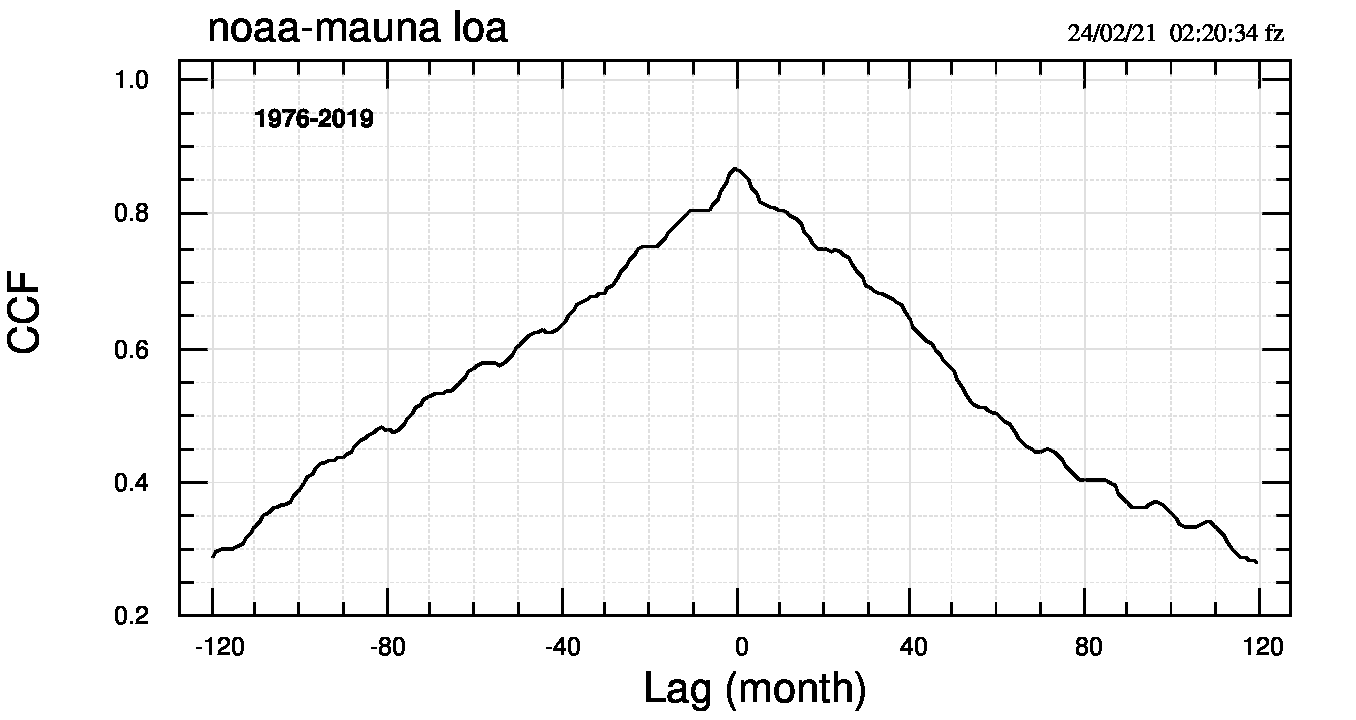
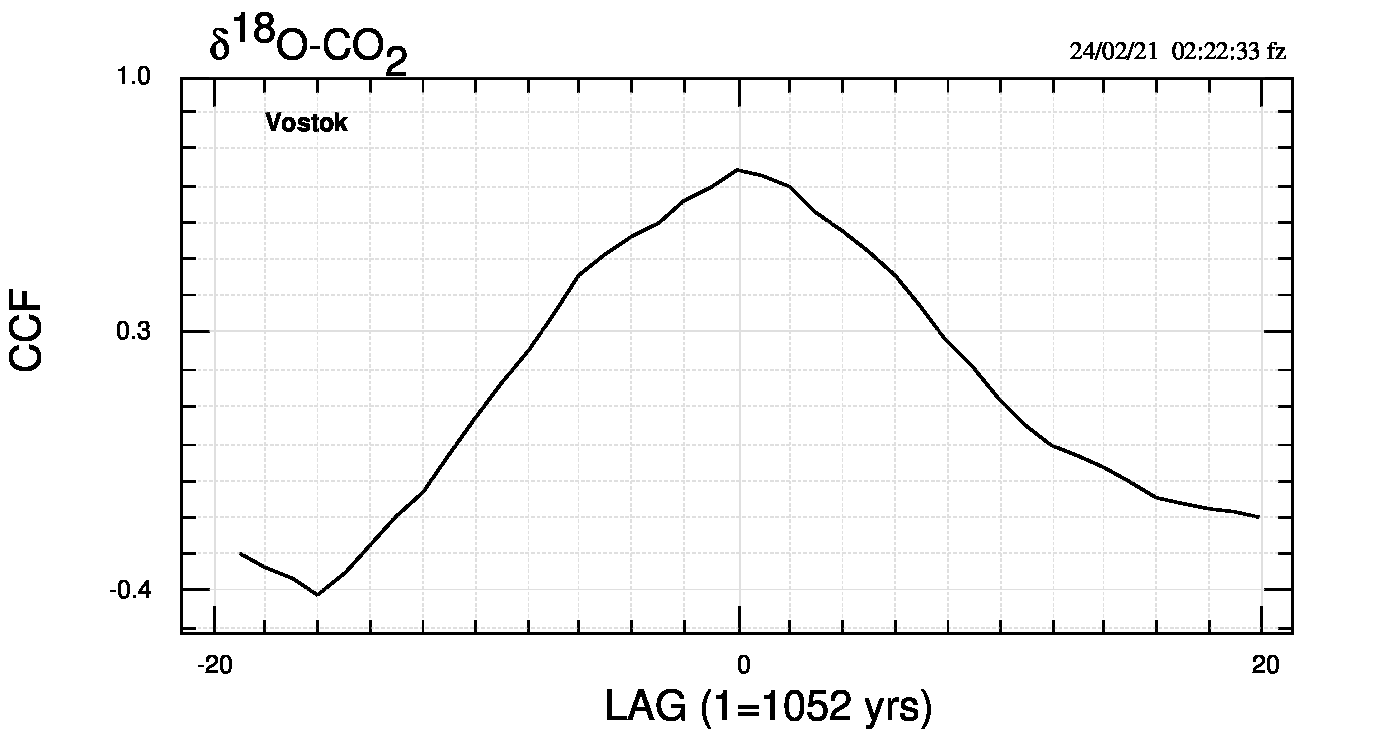
Nei due casi per i quali ho calcolato la funzione di cross-correlazione (CCF), e cioè 1976-2019 e “Vostok” (figure 2 e 3), non sembra esistere una evidente relazione tra chi precede e chi segue tra le due variabili.
Commenti conclusivi
L’equazione (3) o (3a) sembra valida (quando è valida) solo in media, mentre la relazione puntuale “la CO2 aumenta e quindi la temperatura aumenta” non funziona, a prescindere dal È nato prima l’uovo o la gallina? (o quale delle due grandezze controlla l’altra), come si vede dai “ghirigori” di figura 1 ma anche dal periodo 1981-2012 della stessa figura, dove ad un continuo aumento di concentrazione di CO2 corrispondono alti e bassi di temperatura che, in tutta evidenza, seguono altre “logiche” rispetto al totale controllo da parte dell’anidride carbonica.
Le funzioni di cross-correlazione di una serie breve e una lunga non mostrano ritardi o anticipi di una variabile rispetto all’altra, anche se nel caso più esteso temporalmente la risoluzione potrebbe essere superiore ad un’eventuale differenza.
Bibliografia
- W.J. Davis: The Relationship between Atmospheric Carbon Dioxide Concentration and Global Temperature for the Last 425 Million Years Climate, 5(4), 76-, 2017. https://doi.org/10.3390/cli5040076
- https://www.ipcc.ch/site/assets/uploads/2018/07/WGI_AR5.Chap_.8_SM.pdf (IPCC WGI AR5, Chap. 8, SM: Anthropogenic and Natural Radiative Forcing, Supplementary Material)
- Thorstein O. Seim, Borgar T. Olsen: The Influence of IR Absorption and Backscatter Radiation from CO2 on Air Temperature during Heating in a Simulated Earth/Atmosphere Experiment, Atmospheric and Climate Sciences, 10-2, 2020. https://doi.org/10.4236/acs.2020.102009
Tutti i dati e i grafici sono disponibili nel sito di supporto

Vorrei porre all’attenzione del signor Zavatti una perla contenuta in un articolo scientifico (parola grossa) fra i tanti rintracciabili in rete a sostegno della tesi dominante dei “credenti”.
https://skepticalscience.com/translation.php?a=161&l=17
Mi ci sono imbattuto andando alla ricerca di prove a sostegno della correlazione tra aumento di CO2 per attività antropica e riscaldamento globale, nell’intenzione di valutare, pur da profano della materia, le argomentazioni portate in tal senso.
Se gli argomenti che la scienza porta a supporto delle proprie tesi sono quelli che si leggono nell’articolo, mi convinco sempre più di quanto l’opinione pubblica sia predisposta a bersi tutto quanto esce dai media, senza assumersi l’onere di usare anche soltanto una piccola parte di cervello nel tentativo di ragionare in proprio.
Per inciso, l’articolo giustifica l’evidente discrepanza novecentesca tra aumento di emissioni umane di CO2 e innalzamento delle temperature medie del pianeta (presenti, come il dottor Zavatti ben conosce, in corrispondenza degli anni ‘40 del XX secolo nonché in altri periodi precedenti e successivi) derubricando il fatto a semplici anomalie transitorie dovute a casuali effetti collaterali. Fantastico. Definiscono anomalie transitorie eventi che abbracciano periodi addirittura più lunghi di quello che valutano stia condizionando il tempo corrente, proprio come se la tendenza attuale non potesse andare incontro a una naturale inversione di tendenza come già accaduto con regolarità in passato. No, la scienza, in base alle proprie infallibili previsioni matematiche ha già stabilito che entro i prossimi vent’anni si scioglieranno i ghiacci delle calotte polari in misura tale da comportare un aumento del livello dei mari di circa sette metri. Fantastico.
La “perla” contenuta nell’articolo è tuttavia quella che giustificherebbe l’abbassamento delle temperature medie terrestri concomitante con il pur imponente aumento di emissioni di gas da parte umana avvenuto circa a metà del secolo scorso. Testuali parole:
“La discrepanza maggiore, centrata nel decennio attorno al 1940, sembra sia da attribuire ad un effetto di riscaldamento prodotto dal sistema con il quale si effettuava il prelevamento dell’aria dei motori nelle navi della flotta USA.”
Ogni commento a riguardo mi pare superfluo. Anche un profano come il sottoscritto è costretto a sbellicarsi dalle risa di fronte a una simile argomentazione.
Che cosa tireranno ancora fuori per giustificare l’ingerenza antropica sul clima globale? Che deriva daii fuochi accesi in massa dai contadini in primavera per bruciare le sterpaglie? O forse tireranno in ballo, mi scuso per la volgarità, i peti collettivi emessi dai miliardi di individui che vivono nell’area indo-cinese?
Mi stupisco davvero dell’ignoranza del gregge e chiedo in tutta umiltà asilo nel villaggio di Asterix, pur carente di competenze in materia di meteo e fattori climatici…
La ringrazio per aver fatto un riassunto dell’articolo: per una questione di salute pubblica (cioè privata, … la mia) non leggo quel blog, falso anche nel nome.
“prelevamento dell’aria dei motori nelle navi della flotta USA“: a parte
un paio di evidenti errori che, se lei ha fatto il copia-e-incolla, sono da
attribuire a SKS, in effetti subito prima della seconda guerra mondiale c’è
stato il passaggio (per la misura temperatura superficiale dell’oceano o SST)
dall’uso del secchio (bucket) all’uso della misura di SST nei condotti che
portavano l’acqua di raffreddamento ai motori delle navi. Questa tecnica,
migliore in principio, ha anch’essa i suoi problemi: vicinanza ai motori e
quindi temperature possibilmente più alte del vero, condotti di raffreddamento
con “pescaggio” diverso (credo a seconda del tonnellaggio della nave: in un
dragamine i condotti sono più superficiali che in una corazzata o in una
portaerei, ma vengono sempre indicate come temperature “superficiali”);
però, appunto i problemi sono nelle temperature più alte, non più basse.
E poi la costanza (o l’abbassamento) delle temperature, nelle serie di
temperature globali (terra+oceano) dipendono anche dalle temperature
terrestri e quindi la “pausa” osservata c’è indipendentemente dai problemi
di misura delle SST che contano poco nella visione complessiva (nei dettagli
hanno certamente un peso di cui tenere conto).
Sono sicuro che il nostro padrone di casa non avrà alcuna difficoltà a “concedere” asilo a chi ragiona con la propria testa (e le competenze non sono correlate alla capacità di usare il cervello). Franco
Caro Franco,
Nella tabella 1 del post l’evento El Nino del 2010 è classificato come molto forte mentre su https://ggweather.com/enso/oni.htm è indicato come moderato.
Se gli eventi molto forti sono effettivamente quelli del 1982-83, 1997-98 e 2015-16 potremmo convergere verso la famosa periodicità lunare di quasi 18 anni sulla quale ci hai illuminato più volte. Il primo dei tre eventi Nino molto forti avrebbe dovuto verificarsi intorno al 1980. Data la complessità del fenomeno del Nino, che è il risultato dell’interazione di numerosi fattori, è quindi difficile trovare sempre una periodicità di circa 18 anni. Il ruolo della luna può infatti essere mascherato da altri fattori che ne ritardano l’espressione, ma non è detto che questo ruolo non esista.
Qui sarebbe interessante indagare la ciclicità di Giuseppe Toaldo (https://it.wikipedia.org/wiki/Giuseppe_Toaldo), cioè il periodo di circa 18 anni che impiega la luna per tornare a proiettare la sua immagine sullo stesso punto della terra (http://www.climatemonitor.it/?p=52806). Quando la luna ritorna sopra il Pacifico del Sud ogni 18 anni circa, la sua forza attrattiva richiamerebbe grandi quantità di acqua calda dall’Australia, innescando un fenomeno di Nino particolarmente forte.
Mi fermo alla formulazione dell’ipotesi, nella speranza che qualcuno possa testarla.
Cari saluti,
Gianni
Caro Gianni,
grazie per aver messo in evidenza l’errore (mio) nella Tabella 1. In effetti El Nino 2010 è moderato con una minuscola invasione nell’area “forte”.
Per la possibilità di identificare un periodo di influenza lunare nelle serie di varia natura, sarei di mio uno di quelli chiamati sdegnosamente “ciclisti” su WUWT, da Willis Eschenbach, da Svalgard e forse da qualcun altro, nel senso che “vedono” ciclicità dappertutto. Il fatto è che non riesco a trovare nelle serie di ENSO nessun ciclo che possa far pensare alla Luna (v. ad esempio http://www.climatemonitor.it/?p=52453 oppure il suo sito di supporto http://www.zafzaf.it/clima/cm142/cm142home.html), a meno di
incominciare, come fanno ad esempio Serykh, Sonechkin e la loro scuola di pensiero, ad usare 3-4 cifre decimali per i periodi e andare a cercare le sub- e super- armoniche di 18 e 18.6 anni. Se facessi così, sono sicuro che potrei trovare per il
1) ciclo di Saros (18 anni) i periodi di
36, 54, 72 anni come super-armoniche
9, 6, 4.5 anni come sub-armoniche;
2) ciclo degli apsidi (8.85 anni)
17, 26.55, 35.4 anni come super-armoniche
4.43, 2.95, 2.2 anni come sub-armoniche
3) ciclo dei nodi (18.6 anni)
37.2, 55.8, 74.4 anni come super-armoniche
9.3, 6.2, 4.65 anni come sub-armoniche
ma poi, come riuscirei a distinguere, ad esempio, 4.65 da 4.5, per restare alla Luna, o da 4.68 anni (la 4.a super-armonica del Chandler Wobble)?
Con quale faccia (di bronzo) potrei dichiarare l’influenza della Luna quando (e se, con l’aiuto di forzature) trovo solo armoniche e mai il periodo principale? Perché, ad esempio seguendo il lavoro di Agosta e il vostro sull’erosività delle piogge (con massimi spettrali nel range 18-20 anni) nel bacino del Po o nel post sulle precipitazioni nei bacini di 15 fiumi inglesi e gallesi (v. http://www.climatemonitor.it/?p=52879 per altri esempi) posso almeno proporre, anche in forma dubitativa, la presenza di massimi lunari e quando ho che fare con ENSO questo non succede mai?
Quando scrivi “Mi fermo alla formulazione dell’ipotesi, nella speranza che qualcuno possa testarla” ti stai rivolgendo a me che questa ipotesi l’ho testata (in CM142 e nel corrispondente CM e ogni volta che ho a disposizione dati legati ad ENSO) senza riuscire a trovare nulla che possa permettermi di fare affermazioni “pro legame Luna-ENSO” in maniera inequivocabile o anche solo dubitativa.
Ti ringrazio per i tuoi commenti, sempre stimolanti. Franco
I grafici di cross correlazione sono ottenuti come convoluzioni dei dati?
I miei ricordi però sono vaghi. Come sarebbe il grafico di una cross correlazione di una serie che anticipa l’altra?
Sì, la cross correlazione è una convoluzione.
Se abbiamo due serie (allineate temporalmente) A e B ,se B precede A la CCF (cross correlation function) è come quelle pubblicate, con il valore a lag 0 spostato nella semi-zona negativa (ha un lag, cioè un ritardo, negativo e quindi un anticipo). Il valore a lag 0 è il coefficiente di correlazione di Pearson. Franco
Mi permetto un commento, ma pregando di non leggervi alcunché di polemico – solo la mia genuina e sicuramente incolta curiosità.
Quale base fisica potremmo invocare per suffragare questa affermazione, che mi sembra centrale per il seguito:
“…cioè una relazione lineare tra variazione di temperatura ΔT e logaritmo naturale del rapporto tra le concentrazioni della CO2 attuale e quella di riferimento.”?
Ad esempio, potremmo assumere come lineare anche la variazione dell’albedo dovuta alla variazione, se esistesse, della copertura media delle nuvole in funzione della temperatura media?
Oppure, cosa potremmo speculare sulla variazione dell’escursione termica giornaliera media al variare della temperatura media, ricordando quanto la copertura nuvolosa media dovuta già alle sole coperture nuvolose di origine convettiva possa essere comparativamente più sensibile all’escursione termica media che al valore assoluto della temperatura media?
In altre parole, se accetto la linearità della relazione menzionata, il resto ha una sua logica, ma procedendo così avrei affidabilmente rappresentato il fenomeno naturale che sto valutando?
Se non ho capito male il suo dubbio, mi chiede se le formule (1) e (2) sono
corrette. Lo sono per l’IPCC (ad esempio AR5, Working Group 1) e, sinceramente,
ho ritenuto che questo fosse sufficiente. La linearità (nel logaritmo) della
(1) e la sua derivazione (3a) sono dati di fatto e non oggetto della discussione
o ipotesi.
Ma sono quasi sicuro di non aver capito il suo ragionamento: se fosse così,
la pregherei di aiutarmi a capire. Franco
Ottimo articolo, come sempre, di Franco Zavatti. Le conclusioni sono in linea con le opinioni di noi “sccettici”.
Grazie. Il suo parere mi conforta molto. Franco