Durante un’esplorazione bibliografica non mirata, mi sono imbattuto nel lavoro Brazdil et al. (2005) relativo allo stato dell’arte della climatologia storica in Europa in cui, tra le molte informazioni disponibili (ovviamente precedenti il 2005), ho notato il grafico della serie delle piene del fiume Moldava (Vltava in ceco), misurate a Praga dal 1500 al 2002. E’ il fiume principale della Repubblica Ceca e si getta nell’Elba.
Riproduco in figura 1 la figura 10 di Brazdil et al.(2005), sottolineando che i dati sono su due scale verticali differenti: un “indice di piena” prima del 1825 e la portata in m3/s successivamente a quella data di inizio delle misure regolari.
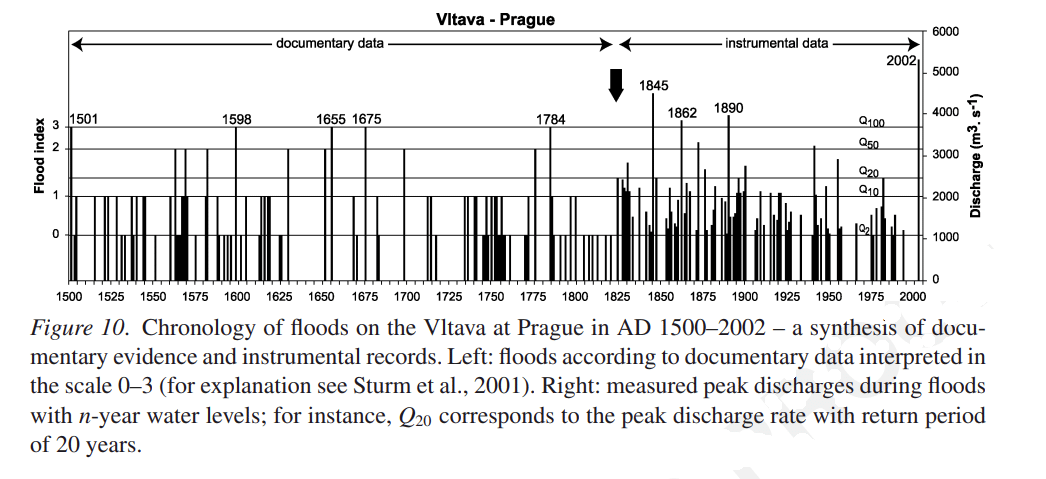
Ho digitalizzato questa figura, usando la sola scala di destra (portata del fiume), e ho prodotto un file di dati, disponibile nel sito di supporto, e la figura 2.

L’osservazione della serie delle piene ci dice che la portata del fiume non segue uno schema regolare: dopo un periodo in cui i massimi sembrano più frequenti (1560-1600), si vede un periodo di circa 80 anni senza piene, intervallato da alcuni (2-3) episodi di piena medio-alta. A questo periodo di situazioni quasi-statiche succede un periodo (ancora di circa 80 anni, ~1825-1900) in cui si osservano alcune tra le maggiori portate della Moldava. Segue un periodo (che sembra complessivamente in diminuzione di portata) fino a fine serie, quando, 2002, si osserva il maggiore flusso della serie; questo massimo viene attribuito ad una piena con tempo di ritorno di cica 500 anni e legata alla piena del 1432, conosciuta come la “piena del millennio”. L’impressione generale che si ricava è quella di un aumento fino a circa il 1860 e poi una diminuzione, in contrasto con l’indicazione dei modelli climatici di un aumento progressivo degli eventi estremi, sia in potenza che in numero.
Lo spettro della serie di piene dovrebbe riprendere anche i periodi di ritorno elencati in figura 1 (Qxx) e in effetti tutti i periodi di ritorno sono adeguatamente rappresentati. Anche il periodo di 187 anni, presente solo nello spettro, trova un riscontro, almeno come ordine di grandezza, nel “passo” delle piene tra 1501 e 1655 (155 anni); 1655 e 1845 (181); 1845 e 2002 (158). Il possibile periodo di 500 anni non viene considerato per ovvi motivi di lunghezza della serie.
Nello spettro si nota anche un massimo di periodo 19 anni che farebbe entrare la portata della Moldava nel novero dei dati influenzati dal ciclo dei nodi della Luna (18.6 anni, v. ad esempio http://www.climatemonitor.it/?p=52692). Ho raccolto nelle due pagine seguenti, e metto a disposizione, tutti i casi che ho analizzato in cui
- gli eventi estremi non seguono il continuo aumento della CO2 (in generale, non seguono l’AGW) e non crescono dal 1850. Pagina degli Eventi estremi
- negli spettri è presente il ciclo dei nodi della Luna (18.6 anni, qui 18-20 anni). Pagina del Periodo 18-20 anni.

Quanto si può dedurre da figura 2, trova conferma nella figura 3 (tratta da Hradecky & Brazdil, 2016) che mostra la frequenza, su base decennale, delle piene in tutti i principali fiumi della regione Ceca: il comportamento schematico è lo stesso per tutti i corsi d’acqua, con aumenti attorno al 1600, un periodo di magra fino a circa il 1700 e un nuovo massimo centrato su 1850-1900, con una diminuzione, in media, fino a fine serie.
Si può dire che i fiumi della regione ceca non mostrano alcuna dipendenza diretta da “cause” continuamente crescenti dal 1850, tipo la concentrazione di CO2 generata da attività umane.
Il confronto tra piene e temperatura media è quasi doveroso: ho usato qui ETA (European Temperature Anomaly, Mariani e Zavatti, 2017) la serie che i lettori di CM trovano nella barra destra e che sicuramente rappresenta la situazione meglio della temperatura dell’emisfero nord o anche della sola CET, relativa ad un’area più ristretta. Ho usato l’aggiornamento al 2020 (qui in temperatura invece che in anomalia) e l’ho confrontato con la serie delle piene.
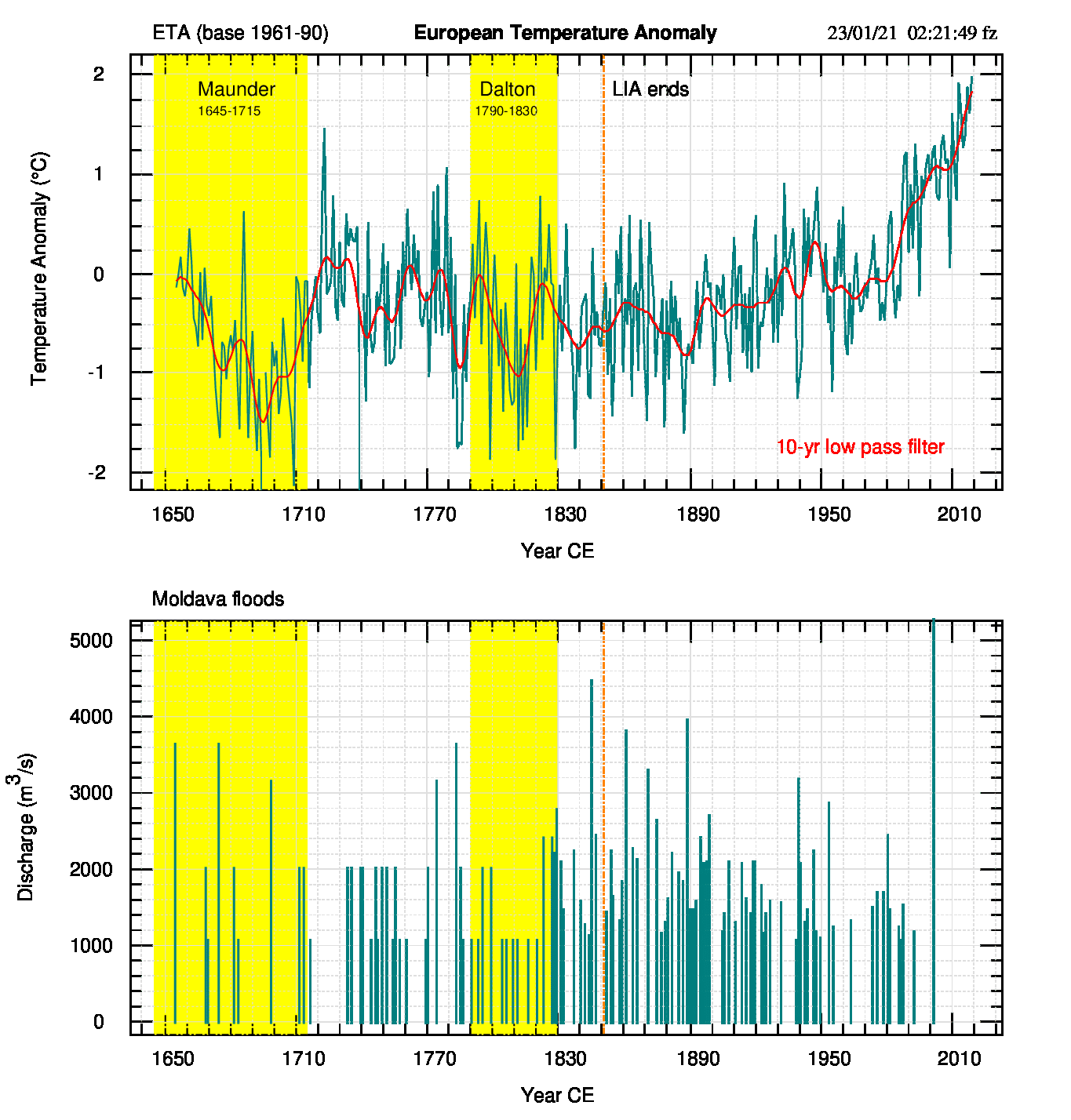
Dalla figura 4 deduco che non sembra esserci un rapporto stretto tra i minimi solari e la portata delle piene (durante Maunder si hanno piene importanti; durante Dalton livelli minimi di portata, con alcuni balzi di media intensità) e che, dopo la fine della PEG (LIA), ad un generico aumento della temperatura corrisponde una altrettanto generica diminuzione media della portata delle piene.
In termini più “giornalistici” l’ultima frase potrebbe essere: ad un aumento della temperatura (causato dall’aumento della CO2, come è ovvio) corrisponde una diminuzione degli eventi estremi (cioè una diminuzione di portata e quindi delle esondazioni), in netto contrasto con le previsioni dei modelli RCP8.5, o anche in accordo con gli stessi modelli, considerando che la diminuzione della portata significa aumento della siccità (o diminuzione delle precipitazioni).
Se qualcuno ha capito qualcosa, alzi la mano.
La mia personale versione del guazzabuglio è: tutto genera tutto, purchè la narrativa non venga falsificata, perché è vera a prescindere dalle prove sperimentali le quali, se in contrasto, sono sbagliate o almeno da rettificare. Un esempio concreto è un articolo su CM che in pratica narra di notizie giornalistiche che affermano cose non presenti nell’articolo scientifico che usano come prova.
Nel lavoro di Bradzil et al., 2005 si legge anche una approfondita disamina del rapporto tra cambiamenti climatici e intervento dell’uomo in vari aspetti: dal fatto che il clima è stato uno dei più potenti fattori nel determinare la storia umana, al fatto che aspetti sociali possono solo essere determinati da fattori sociali (quindi senza influenza del clima). Alcuni scienziati, tra cui Le Roy Ladurie che nel suo libro del 1967, L’histoire du climat depuis l’au mil scrive “Nel lungo periodo le conseguenze del clima sulle vicende umane sembrano essere leggere, forse trascurabili, e certamente difficili da trovare”, hanno tentato una mediazione tra gli estremi descritti più in alto.
Bradzil e colleghi discutono anche il fatto che “clima” e “storia” sono termini omnicomprensivi, situati ad un livello di astrazione talmente alto che la loro relazione non può essere studiata seguendo il metodo scientifico; è necessario separare i due argomenti in analisi su scale inferiori e più pratiche, ad esempio mettendo in relazione attività umane specifiche e variabili climatiche, produzione agricola e piovosità, ad esempio. Non voglio espandere ulteriormente questa discussione e invito a leggere il lavoro, anche se è vecchio di quindici anni, liberamente disponibile al link di ResearchGate in bibliografia, che certo è più interessante di ogni mio possibile riassunto, anche se non si dovesse essere d’accordo sul modo di trattare l’argomento.
Nota aggiuntiva: a distanza di tre mesi dalla scrittura di questo post, nell’analisi delle piene del fiume Tago (Penisola Iberica) ho trovato un brevissimo articolo di Vaquero (2004) che commenta la frequenza decennale (n. di eventi in bin di 10 anni) delle piene di quel fiume, pubblicata da Benito et al. (2003). Vaquero sottolinea che la frequenza può essere considerata un proxy dell’attività solare e fa notare che Sole più attivo corrisponde a maggiore frequenza di piene e viceversa. Per verificare questa affermazione nel caso della Moldava, ho calcolato la frequenza decennale dalla figura 1 e l’ho associata ai minimi solari nella figura 5.
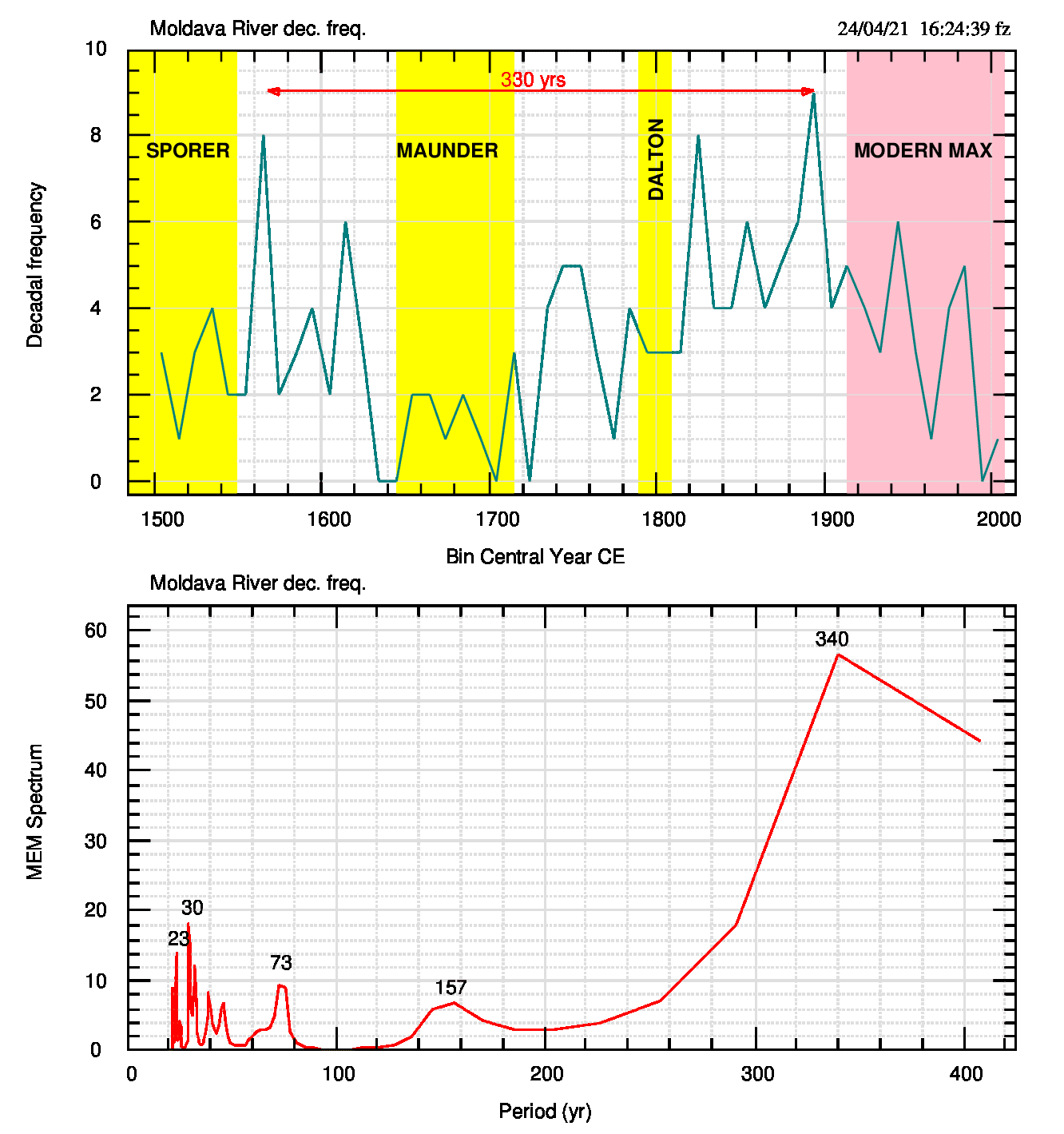
Ad un primo esame, la situazione della Moldava sembra confermare quanto affermato da Vaquero per il Tago (minore attività solare=minore frequenza di piene), la cui serie si estende per più di 300 anni oltre quella della Moldava (dal 1100 al 2000).
- Benito G., Diez-Herrero A., Fernandez de Villalta M.: Magnitude and frequency of flooding in the Tagus basin (Central Spain) over the last millennium., Climatic Change, 58, 171-192, 2003. testo completo a: Research Gate
- Vaquero, J.M.: Solar signal in the number of floods recorded for the Tagus river basin over the last millennium, Climatic Change, 23-26, 2004.
Bibliografia
- Rudolf Brázdil, Christian Pfister, Heinz Wanner, Hans Von Storch and Jürg Luterbacher: Historical Climatology in Europe – The State of the Art , Climatic Change, 70(3), 363-430, 2004 https://doi.org/10.1007/s10584-005-5924-1. Also: https://www.researchgate.net/publication/201169368_Historical_ Climatology_In_Europe_-_The_State_Of_The_Art
- Hradecky Jan & Brazdil Rudolf: https://is.muni.cz/el/sci/jaro2019/Z0151/Hradecky_Brazdil_2016_K3.pdf flood frequencies of Czech Lands Rivers
- Mariani L., Zavatti F.: Multi-scale approach to Euro-Atlantic climatic cycles based on phenological time series, air temperatures and circulation indexes , Science of the Total Environment, 593-594, 253-262, 2017. doi:10.1016/j.scitotenv.2017.03.182
Tutti i dati e i grafici sono disponibi nel sito di supporto


[…] la 2A a cui è stata aggiunta la frequenza decennale della Moldava (Bradzil et al., 2005, v. anche questo post su CM) che, nelle sue linee essenziali non si discosta dallo schema proposto da Vaquero. Durante il […]
Lavoro interessante ma sono curioso di sapere come gli autori siano riusciti a confrontare le piene del XVI secolo con le attuali a fronte di un irrigimentazione dei corsi d’acqua avvenuta fra il XIX ed il XX secolo. Considerando anche il prelievo per usi agricoli civili e industriali e il dragaggio dei fondali per la navigazione e il prelievo di inerti.
Non conosco i dettagli operativi dei metodi usati in idrologia per derivare le piene attuali, dopo le varie operazioni sui fiumi, dettate dall’esigenza di sicurezza e di utilizzo delle acque, ma so che la ricerca storica in questo campo è attenta all’ambiente circostante e alle sue variazioni, anche antropiche. Da ignorante, mi viene in mente la regolazione del livello del Garda che si cerca di mantenere il più possibile costante per evitare
allagamenti delle aree rivierasche: oltre a misurare il livello del lago, si misura anche il flusso di scarico verso il Mincio (e l’Adige, in caso di piene eccezionali) e da questo si risale al livello.
Penso che tecniche simili, accompagnate da misure pluviometriche sicuramente legate alla portata dei fiumi del bacino, siano in grado di correggere possibili variazioni dovute all’uomo (a mio parere molto variabili, nel tempo e nello spazio). Anche le misure di flusso, a monte delle modifiche, e modelli orografici del territorio penso possano contribuire alla ricostruzione di serie storiche del periodo moderno. Franco
vorrei farvi sommessamente notare che il nostro pianeta non dispone di regolarità.
Certo, analizzando i dati con strumenti matematici definiti “statistici”, probabilmente è possibile dimostrare regolartità associate.
Ma vi sono così tante variabili che è ben difficile determinare una immediata relazione causa -effetto.
Se durante i periodi freddi della Peg i fiumi erano in piena durante la primavera-estate, a causa delle forti precipitazioni nevose in inverno, probabilmente durante i periodi caldi le piene avvengono in estate-autunno, ma una regolarità è ben lontana.
da anni che seguo il blog ed una cosa ho riscontrato: non si può mai dire la parola “fine”.
Anche nella raccolta dei dati vi possono essere delle incertezze (dipendenti dallo strumento e dall’osservatore, vi è tutta una teoria degli errori!) per cui vi è notevole incertezza nel ricostruire il passato utilizzando le “misure” attuali.
Vi è questo studio Current European flood-rich period exceptional compared with past 500 years hhttps://www.nature.com/articles/s41586-020-2478-3
Ebbene, tra i dati elaborati vi sono così tanti “no data” che veramante non riesco a comprendere come si possano trarre delle conclusioni anche approssimative, per non dire definitive.
Se l’attuale ricerca scientifica si limita dare in pasto ad algoritmi i dati….. beh, possiamo concludere che la scienza è cosa morta?
O si conoscono le relazioni causa -effetto oppure si masturbano i dati per cercare di trarre delle inferenze.
Io, personalmente, della scienza statistica non ho nessuna fiducia…. Trilussa docet.
Potrei cominciare a rispondere dicendo la banalità che “niente è eterno” … ma che le regolarità ci sono e durano nel tempo quanto viene loro permesso dalle altre condizioni delle forze e della materia che le circondano e che le vincolano.
Se guardiamo la figura 2 dell’articolo citato (Blöschl et al., 2020) vediamo bene che, malgrado le incertezze e la mancanza di dati, esistono delle regolarità denotate da bande di maggiore frequenza delle piene. Non ho avuto modo di verificare i periodi di queste regolarità, e in particolare di vedere se coincidono con i massimi (o non-minimi) solari, ma ci sono. Ricordo che ho già scritto (mi sembra proprio in questo post) che non vedevo nessun segnale solare nello spettro delle piene: l’ho visto solo dopo aver costruito la frequenza decennale delle piene e non mi meraviglierei se i massimi di figura 2 di Bloschl non coincidessero con i massimi solari, ma, ripeto, le regolarità ci sono.
I dati sono frammentari? I dati sono quello che sono e se ricercatori come gli autori (conosco di fama alcuni di questi e via mail altri: Camuffo, Bertolin, Bradzil, Benito e li considero persone serie) tentano di ricavare informazioni (parziali? con forti errori? meno certe delle misure di laboratorio? certo) credo si debba apprezzare la loro serietà nel tentare di estrarre qualcosa da situazioni vaghe. Non credo sarebbe meglio non avere
affatto queste informazioni.
E’ proprio in queste situazioni di incertezza e di necessità di acquisire informazioni dove ci sono poche basi “fisiche” che la statistica serve e, diciamocelo, Trilussa, che amo molto e che negli anni passati ho letto intensamente, non “docet” proprio niente se non l’idea che della statistica ha chi non la conosce (ad esempio il popolo minuto di Trastevere, nel suo
caso).
Anche la figura 5 del post (e le figure di un altro post che verrà pubblicato, credo, verso la fine di agosto) dà indicazioni di massima di una relazione tra cicli solari e livello di piena e non si sogna minimamente di associare ogni piccola crescita o discesa del grafico a una “situazione” solare, quasi a cercare di ricostruire la fisica solare “istante per istante” dall’osservazione delle piene.
Nel commento si cita la teoria degli errori: dovrebbe quindi essere chiaro che la certezza non esiste, tranne per chi ha bisogno di manifestarla (i politici, ad esempio, che fanno un dovere dell’esternare una certezza che non possono avere, ma questo non ci interessa qui).
Se qualcuno, nel nostro ambiente, pretende di averla, sta sbagliando qualcosa.
Saluti. Franco
Premetto che non amo la statistica. Rispetto ad altre branche della matematica è quella che mi appassiona meno, ma ci serve.
Ci serve perché consente di vedere più chiaramente la ove non si vedrebbe niente. E’ un mezzo per capire linee di tendenza che altrimenti ci sfuggirebbero. La stessa teoria degli errori è, in senso lato, un algoritmo statistico. Essa ci dice solo che la media dei valori di una serie di misurazioni è il “valore più probabile” di quella misura. E la media (aritmetica, pesata, ecc.) è uno dei principali indicatori statistici.
Lo stesso “principio dei minimi quadrati” che consente di individuare una curva di regressione all’interno di un insieme di dati, è un algoritmo statistico.
Nessun tecnico, ricercatore o chiunque abbia a che fare con i dati numerici, quindi, può fare a meno della statistica.
.
Ci sono, però, le esagerazioni. E queste esagerazioni sono le correlazioni quando vengono spacciate per causazione. Questo approccio io contesto alla radice, ma non la statistica che genera la correlazione. L’algoritmo che consente di calcolare il tempo di ritorno di un sisma o di una piena va benissimo, basta che non lo si utilizzi per prevedere quell’evento. Per restare nel campo dei terremoti, le strutture civili vengono progettate per sismi che hanno tempi di ritorno confrontabili con la vita media della struttura stessa, ma in modo tale che anche in presenza di sismi caratterizzati da tempi di ritorno più lunghi, non collassino, determinando la morte degli utilizzatori.
A prima vista questo potrebbe sembrare un assurdo: si cercano regolarità in un fenomeno che di regolare non ha nulla, ma non è così. Noi non sappiamo quando il sisma distruttivo si verificherà, ma sicuramente si verificherà in quanto i dati dimostrano che dopo ogni “tot” anni questi fenomeni si verificano. E questo “tot” ce lo fornisce l’analisi statistica dei dati. Personalmente mi aspetto da un momento all’altro un terremoto nella mia zona: i tempi di ritorno sono maturi, anzi è pure in ritardo. Con ciò non mi sognerei mai di prevedere una data in cui tale sisma si verificherà.
.
Le regolarità le troviamo, infine, anche in quei fenomeni che sembrano caotici: la teoria cinetica dei gas trae origine dallo studio dei moti browniani che sono caotici per antonomasia. Eppure da questi moti caotici emergono le leggi della termodinamica che consentono di determinare il funzionamento di sistemi termodinamici. E tutto ciò grazie alla statistica.
E questo senza addentrarsi nel campo minato del caos deterministico e degli attrattori che lo caratterizzano: anche in questo caso la regolarità emerge dal caos.
Ciao, Donato.
Grazie,
ho scoperto questo blog su twitter.
Non sono un esperto quindi non so dire se quanto scritto è formalmente corretto o meno, tuttavia il fatto che vangano pubblicati non solo i risultati ma anche i dati di partenza è un punto su cui si dovrebbe riflettere molto.
Grazie a lei per apprezzare la disponibilità dei dati utilizzati. Devo anche dire che, avendo un server web nel quale depositare i miei dati, sono facilitato in questa operazione che, comunque, ritengo necessaria per permettere una critica seria a quanto scrivo. Franco