L’indice TPI (Tripole Pacific Index) si basa sulla differenza tra le SST (anomalie) mediate sull’area del Pacifico centro-equatoriale e la media delle SST nel Pacifico di Nord-Ovest e di Sud-Ovest. E’ un indice semplice da calcolare per tracciare la variabilità decennale associata ad IPO, l’oscillazione interdecennale (interdecadale nella terminologia inglese) del Pacifico.
Non usa la PCA (analisi delle componenti principali), più difficile da realizzare, ed è molto simile agli indici calcolati in precedenza con la PCA; è anche più vicino agli indici usati per tracciare El Nino, come Nino 3.4, e viene fornito in unità fisiche (°C). IPO e PDO (Pacific Decadal Oscillation) sono due modi di definire le oscillazioni interdecennali e decennali del Pacifico e sono strettamente legate tra loro, al punto che PDO viene considerata il nodo nord-pacifico dell’IPO complessivo.
Henley et al., 2015 presentano un lungo elenco delle influenze che PDO e IPO hanno sul clima mondiale, dal Nord America all’Asia orientale, dall’Australia al Sud America, e anche sulle produzioni agricole.
Da notare anche che il riscaldamento accelerato del 1976-2000 e le due pause 1945-1975 2000-2013 coincidono in maniera accettabile con le fasi positiva (calda) e negativa (fredda) di IPO e che quindi l’indice TPI (a me finora del tutto sconosciuto) va guardato con attenzione. Intanto mostro, nella figura 1, l’immagine di apertura del sito psl.noaa dove sono disponibili le serie numeriche di TPI.

Dato che l’indice deriva dalla SST (dalla sua anomalia, indicata da “A”),
| TPI = | SSTA2-(SSTA1+SSTA3)/2 |
|---|
è possibile calcolarlo usando diverse serie di temperature superficiali marine; qui ho scelto di usare noaa-ersst V.5 (che indico con noaa), hadisst1.1 (hsst) e, come confronto, la serie hadsst2 (had2) indicata da Henley e collaboratori nel loro lavoro (più breve delle altre per motivi temporali, iniziando nel 1870 ed essendo il lavoro del 2015). Le serie annuali sono disponibili nel sito di supporto.
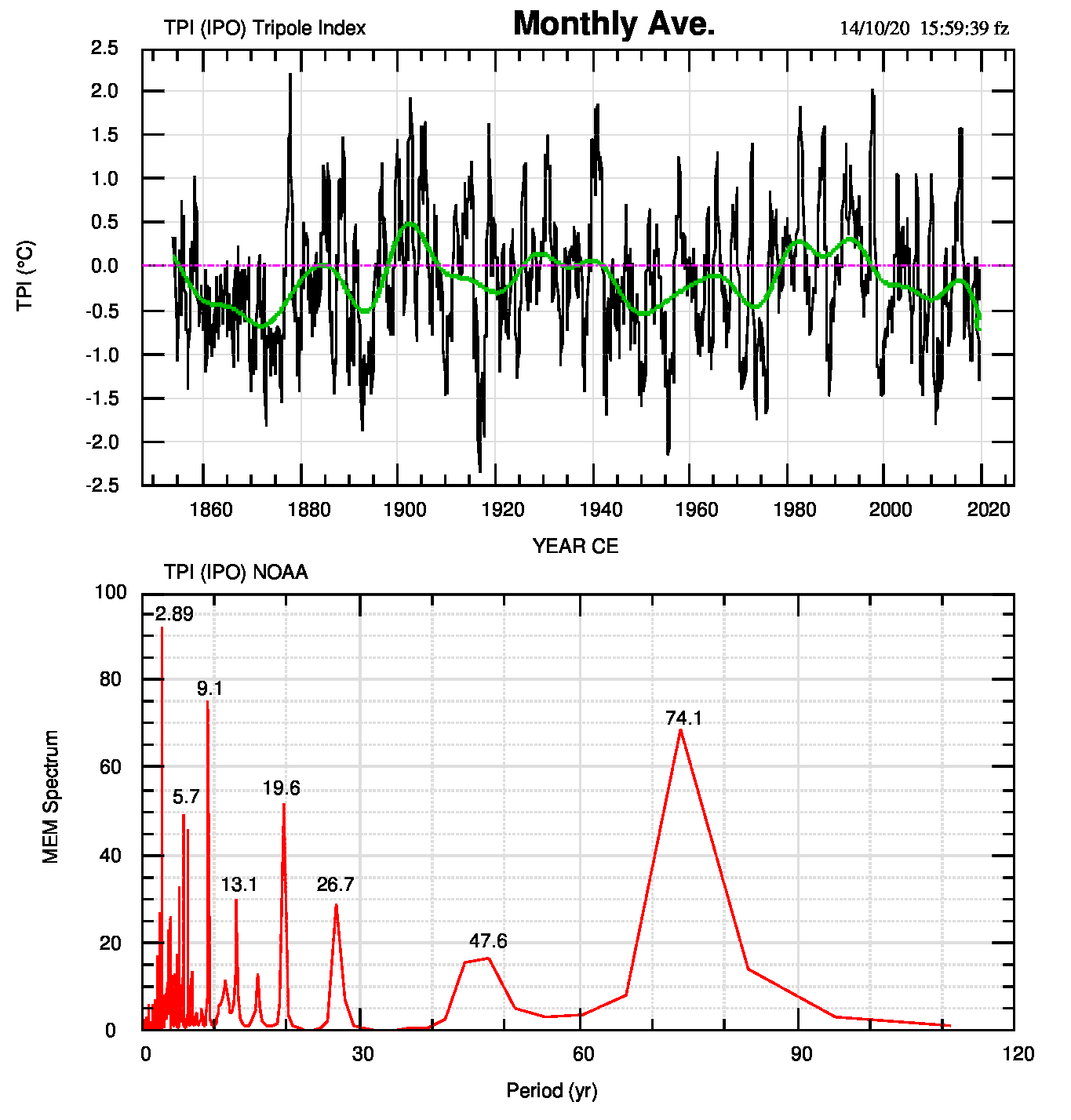
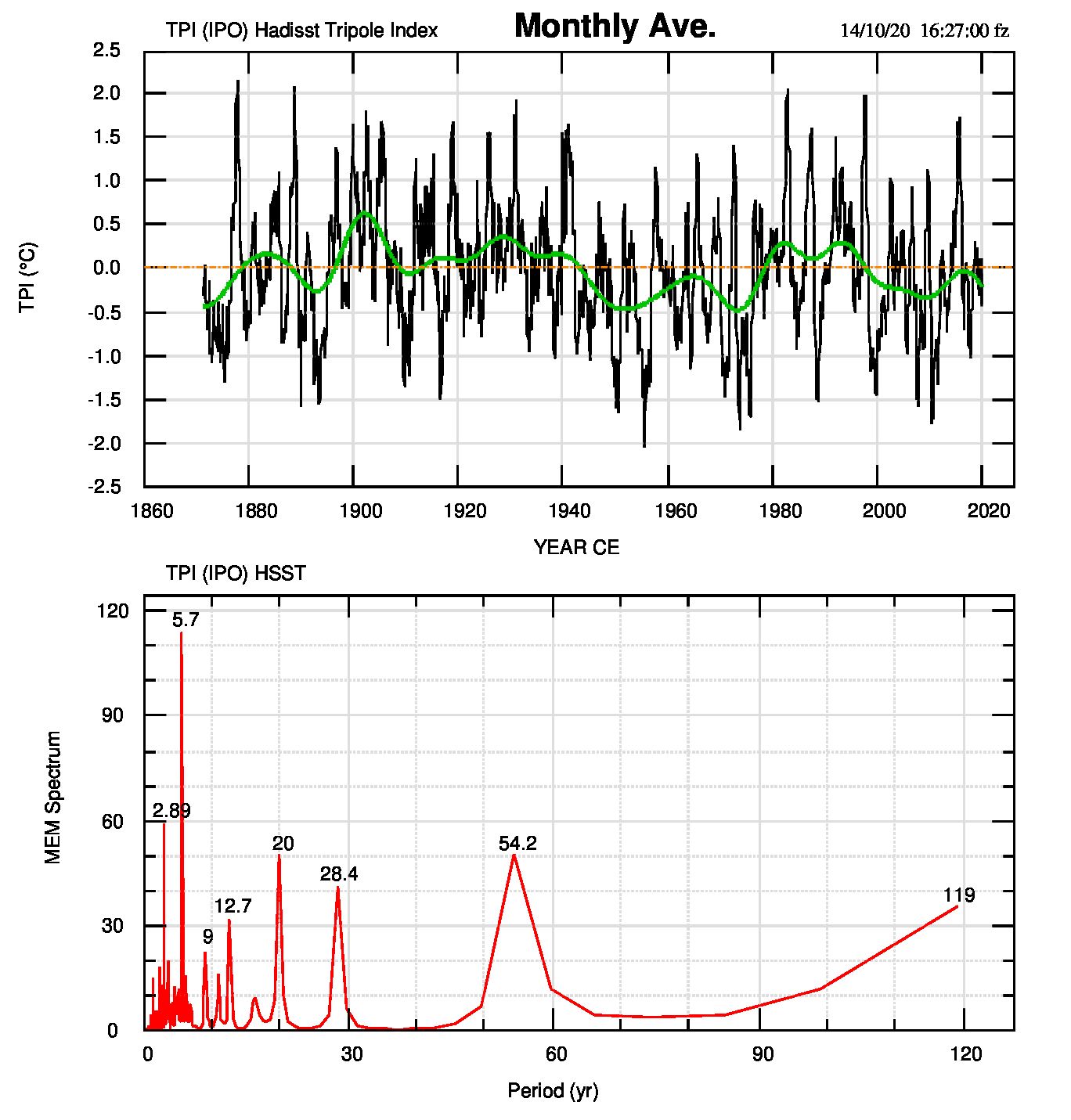
L’indice IPO (che qui rappresentiamo con TPI) si configura su una scala multi-decennale con fasi della durata di 20-30 anni.

Le serie e i loro spettri presentano una buona concordanza che viene meglio sottolineata dalla sovrapposizione, in figura 5, delle tre figure precedenti.
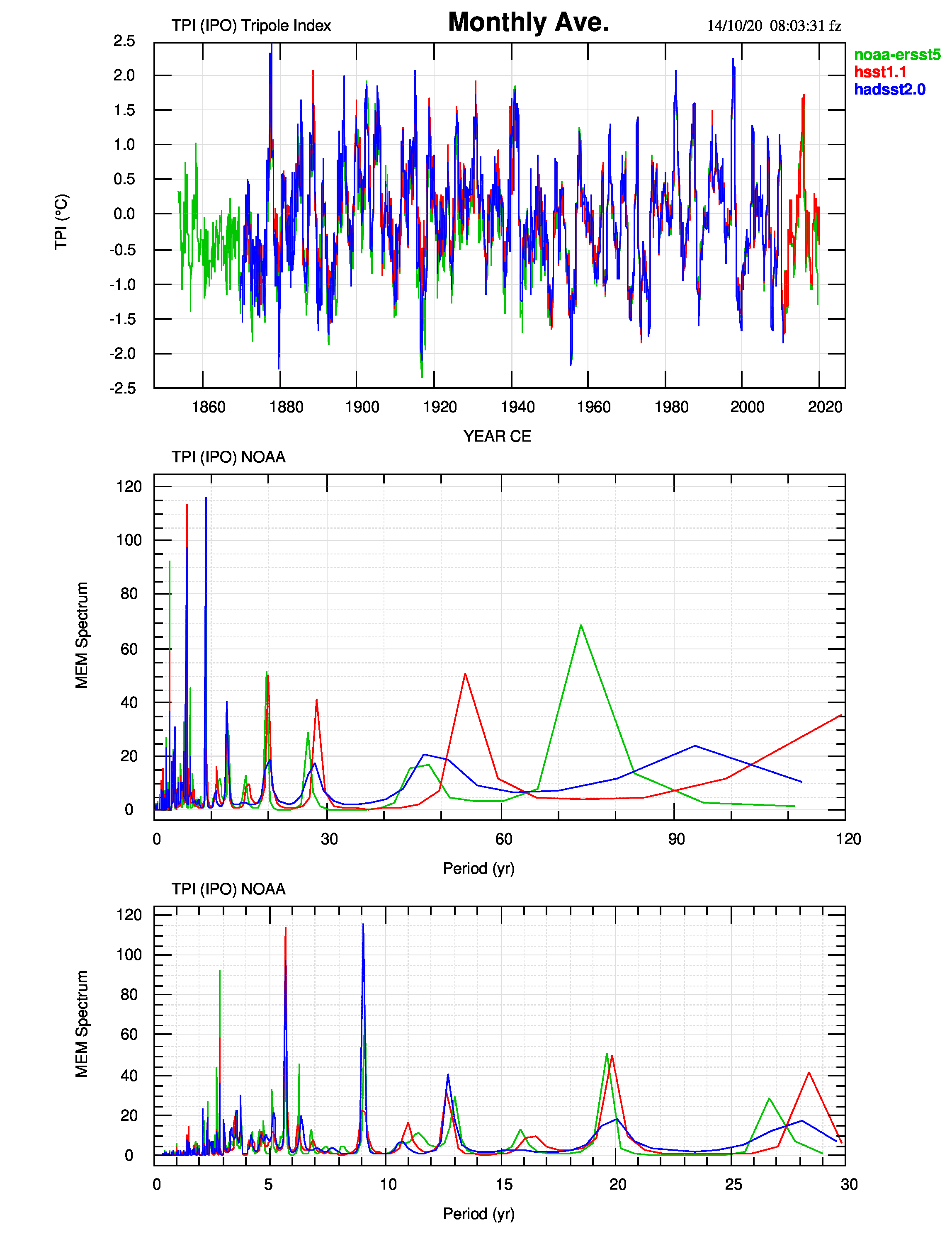
Gli spettri mostrano una notevole uniformità nei periodi fino a 40-45 anni. I periodi più lunghi sono meno compatti e non sempre identificati con sicurezza: in almeno un caso, del massimo spettrale resta solo un cambiamento di pendenza.
In tabella 1 elenco i singoli periodi nei tre TPI. Si può notare la compattezza dei risultati attorno ai periodi “noaa” elencati. I periodi derivati dagli spettri degli altri due TPI possono essere di poco diversi. Solo i picchi di periodo maggiore mostrano una diminuita compattezza, nel senso che sono presenti in una sola serie e in un caso in due.
| P(yr) | NOAA | HSST | HAD2 |
|---|---|---|---|
| 2.89 | X | X | X |
| 5.7 | X | X | X |
| 9.1 | X | X | X |
| 13.1 | X | X | X |
| 19.6 | X | X | X |
| 26.7 | X | X | X |
| 47.6 | X | X | |
| 54.0 | X | ||
| 74.0 | X | ||
| 93.7 | X | ||
| 119.0 | X |
Ma la funzione di autocorrelazione (ACF) di TPI mostra un esponente di Hurst (H=0.982, in realtà un suo limite inferiore) che identifica la presenza di memoria a lungo termine. Ho quindi calcolato la derivata prima numerica della serie TPI-noaa e poi il suo spettro mem (v. ad esempio http://www.climatemonitor.it/?p=47359) e il risultato si vede in figura 6.
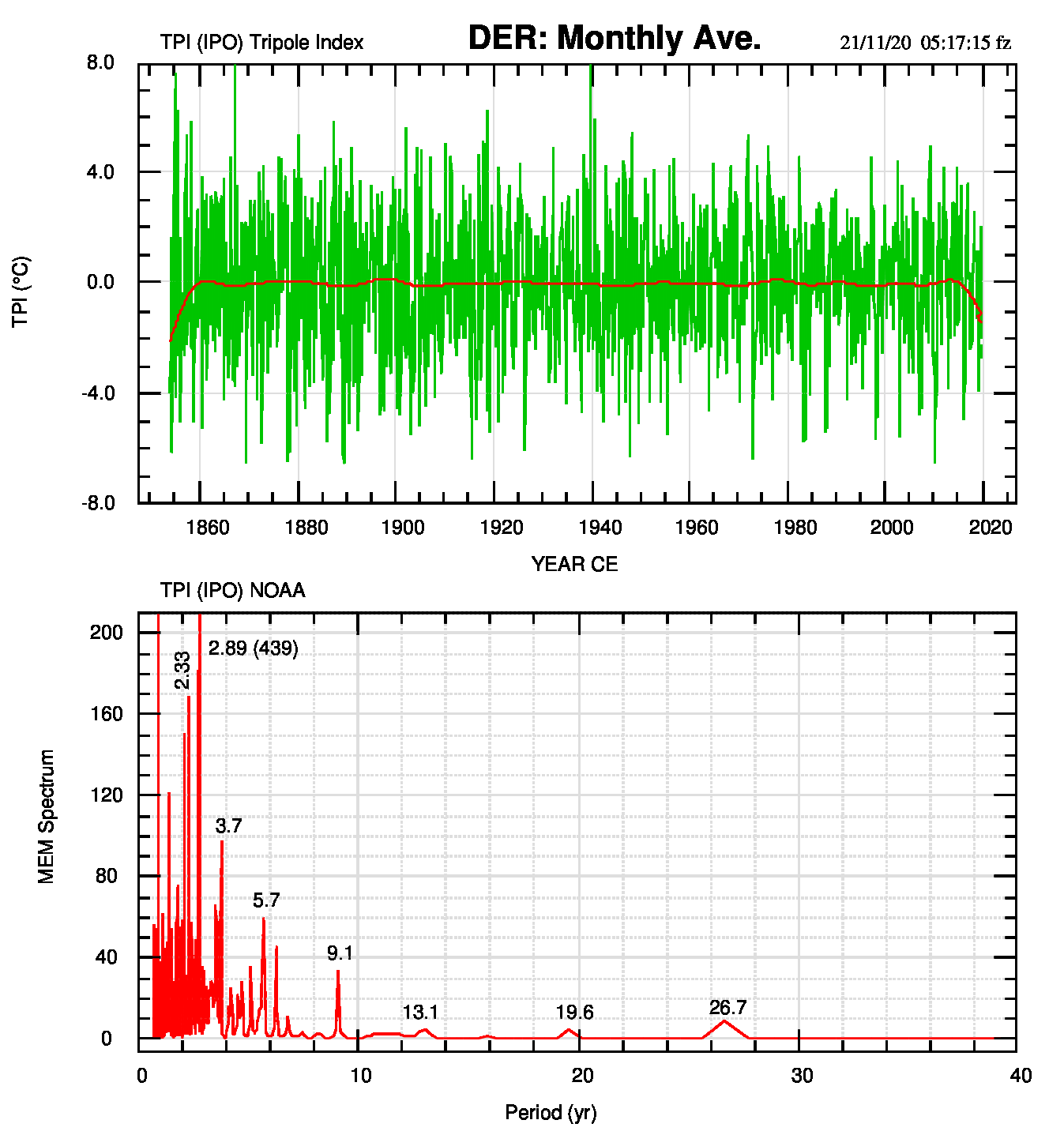
Fig.6: Come figura 2, ma usando la derivata prima numerica (DER) del file dei dati per diminuire la distorsione dovuta alla memoria a lungo termine. La stessa figura con scala verticale del quadro superiore uguale a quella di figura 2 può essere usata per un confronto originale-derivata.
Da notare
- la diminuzione in ampiezza della struttura di TPI (linea rossa) che indica maggiore indipendenza dei dati (o ACF più stretta) e
- la modifica dello spettro, dove acquisiscono importanza i periodi più brevi pur restando una (debole) informazione sui periodi più lunghi.
- Il calcolo della derivata numerica (o delle differenze) è una delle tecniche usate per rimuovere il ciclo stagionale dalle serie temporali. La figura 6 mostra la struttura di TPI (IPO) senza memoria a lungo termine ma anche quasi senza il ciclo stagionale e quindi evidenziando i cicli di oscillazione propri. È questo il senso della diminuita potenza dei cicli di periodo più lungo (13.1, 19.6, 26.7 anni) e della accresciuta potenza dei periodi più brevi (2.89, 3.7, 5.1, 9.1 anni): la destagionalizzazione fa emergere i cicli che compaiono nella funzione di autocorrelazione (estesa qui a lag=180 mesi e con i massimi in anni indicati dalle frecce) delle derivate. In particolare, l’oscillazione più ampia e visibile nella ACF, a 36 mesi (3 anni), identifica il massimo spettrale a 2.89 anni e, in modo più smussato, anche 28, 73, 132, 161 mesi (2.33, 6, 11, 13 anni); per curiosità, e anche per mostrare la sensibilità della ACF, un minuscolo massimo (un’ondulazione nella ACF osservata) a lag=107 mesi indica il massimo spettrale a 9 anni (107 mesi/12).
Il massimo spettrale a 2.87-2.89 anni
Periodicamente ritorna nelle mie analisi il massimo spettrale a 2.87 (qui 2.87 e 2.89) anni, identificato da Donato Barone nelle temperature globali (terra+oceano) NOAA, con un commento a un mio post di quasi otto anni fa.
Nella tabella (non più aggiornata, da questa pagina web) avevo raccolto le serie nel cui spettro è presente o no il massimo in questione che sembra essere legato a El Nino (spettro) o che, almeno, si trova nell’intervallo dei periodi (2-9 anni) più significativi del suo spettro. Anche in questo caso, si conferma l’idea che questo massimo sia legato all’oceano, come avevo ipotizzato nell’analisi già citata e non, ad esempio, al Sole o all’influenza lunare: in effetti, con la moda che sta prendendo piede, soprattutto da parte di ricercatori russi ma non solo russi, si potrebbe dire che il picco a 2.87 anni può essere visto come la quarta sub-armonica (2.79 anni) del ciclo delle macchie solari (11 anni) oppure la terza sub-armonica (2.95 anni) del ciclo lunare degli apsidi (8.85 anni).
Per me questo atteggiamento significa voler “tirare per le orecchie” i dati allo scopo di giustificare ipotesi già costituite; ho descritto le mie perplessità nel recente http://www.climatemonitor.it/?p=53559 e pertanto non penso di dover sottolineare ulteriormente la questione.
Commenti conclusivi
Questo post si configura come un’informazione generale su TPI (IPO), cioè sull’indice (forse può essere chiamato “super-indice”) che interessa una parte molto estesa dell’Oceano Pacifico. L’oscillazione decennale del Pacifico (PDO)
“can be regarded as the North Pacific node of the Pacific-wide IPO (Power et al. 1999; Folland et al. 2002).“
- (Henley et al., 2015)
può essere considerata una sua parte e quindi, data l’importanza di PDO nell’influenzare il clima globale, è importante conoscere anche le caratteristiche complessive sia di IPO che della sua realizzazione TPI.
Ho cercato di mostrare questo “indice a tre poli” (figura 1), utilizzando tre serie di temperature superficiali marine (SST) e confrontando le serie e i loro spettri.
Le caratteristiche di TPI (IPO) e i loro legami con le varie situazioni meteorologiche sono ben descritte da Henley et al., 2015 e io le ho riassunte sommariamente.
Dopo un tempo abbastanza lungo, durante il quale non lo avevo più incontrato (e neanche cercato), con l’indice TPI è riapparso un massimo spettrale individuato circa otto anni fa nelle temperature globali NOAA (GHCN): ne ho approfittato per commentare brevemente la sua presenza che, nello spettro del TPI derivato da noaa-ersst V.5 e corretto per la memoria a lungo termine, è particolarmente potente.
Bibliografia
- Henley, B.J., Gergis, J., Karoly, D.J., Power, S.B., Kennedy, J., & Folland, C.K. (2015). A Tripole Index for the Interdecadal Pacific Oscillation. Climate Dynamics, 45(11-12), 3077-3090. http://dx.doi.org/10.1007/s00382-015-2525-1. Accessed on 10.08.2020 at “/data/timeseries/IPOTPI”.
Tutti i dati e i grafici sono disponibi nel sito di supporto.
Il post con un’analisi più dettagliata del massimo a 2.87 anni si trova qui, su CM


Caro Franco,
leggendo i tuoi articoli si rafforza sempre più la mia idea relativa al sistema climatico: un sistema dinamico non lineare caotico. Ogni tanto emergono delle regolarità che, però, tendono a variare a seconda delle serie che si prendono in considerazione.
In questo articolo hai preso in esame tre serie di dati e per ognuna di esse hai individuato dei periodi. Confrontando tali periodi, si vede che essi tendono a “slittare” gli uni rispetto agli altri: i massimi spettrali riferiti alle serie, tendono a non coincidere. Nel nostro caso sono i periodi più lunghi ad avere questa tendenza, ma in altri casi che hai esaminato in passato, la situazione si ripete per periodi più brevi.
.
Potrebbe sembrare paradossale, ma questo fatto mi conforta, perché dimostra che il comportamento del sistema climatico non è prevedibile in modo semplice. Ciò significa che tutti i discorsi che si fanno circa la prevedibilità dei cambiamenti climatici, sono piuttosto campati per aria.
Detto in altri termini, le interazioni tra le variabili che caratterizzano lo stato del sistema climatico, sono talmente complesse, da sfuggire a qualsiasi forma di prevedibilità, tanto nel breve che nel lungo termine.
.
Le forzanti astronomiche, per esempio, esercitano la loro influenza sul sistema climatico, ma i loro effetti sembrano filtrati dalle varie componenti del sistema, per cui le tracce di tali azioni risultano piuttosto elusive: in una serie di dati emergono delle ciclicità, in altre serie le ciclicità sono più o meno diverse.
Questo potrebbe significare che esistono diversi livelli di complessità del sistema climatico e quelle che noi riusciamo a misurare, potrebbero essere delle grandezze emergenti da grandezze più fondamentali che, forse, ignoriamo del tutto.
.
Questi stati fondamentali, potrebbero essere i famosi attrattori che tendono a stabilizzare il sistema climatico nello spazio delle fasi e che si palesano attraverso le ciclicità che man mano scopriamo nelle serie di dati. E potrebbero, alla fine, spiegare il perché questi benedetti periodi tendono a fare i capricci.
.
Le mie sono, ovviamente, delle ipotesi. Il tuo impagabile lavoro di ricerca tende, però, a rafforzare queste mie idee. E di questo non ti ringrazierò mai abbastanza.
Ciao, Donato.
Caro Donato,
punto di vista molto interessante il tuo, che sarebbe altrettanto interessante sviluppare. Se tu avessi tempo e voglia di fare un tentativo, potresti di certo contare anche sui miei dati (oltre quelli disponibili in letteratura). Pensaci …
Io in questo post ho cercato di farmi un’idea sul TPI (prima del tutto sconosciuto) e di vedere come si comporta insieme al suo spettro. Ho avuto orizzonti meno ampi dei tuoi e mi sono dedicato a capire ancora una volta quale è l’effetto della memoria a lungo termine sullo spettro.
L’esistenza del massimo a 2.87 anni in queste serie è stata una sorpresa che ho voluto sottolineare ma che è un “effetto collaterale”, meno importante rispetto al fatto che la memoria a lungo termine (cioè l’autocorrelazione della serie) sembra trasportare potenza verso i cicli di periodo più lungo e che la sua
“correzione” restituisce importanza ai massimi spettrali El Nino-like (da 2 a 9 -12 anni). Ciao. Franco
La mamma climatologa ed i figli
(breve racconto sulla media)
Pierino e Pierina frequentano la stessa scuola, la stessa classe ed hanno gli stessi identici insegnanti.
A fine anno scolastico Pierina mostra un sorriso pieno di gioia.
– Pierina – dice la mamma climatologa – come è andato quest’anno scolastico?
– Mamma, sono stata promossa.
– Brava Pierina e che media hai avuto?
– La media del 6, mamma.
Dopo un po’ arriva Pierino, con una faccia triste e sconsolata.
– E tu, Pierino, come mai sei così imbronciato? Che media hai avuto?
– Mamma, ho avuto la media del 6.
– E perchè sei così triste? Sarai stato promosso anche tu…
– No, mamma, sono stato rimandato in due materie.
Morale della favola… la lascio ai lettori.
Si ringrazia Trilussa per lo spunto… statistico.
Nonostante le medie climatiche più alte… nell’America del Nord si verifica un’estensione di neve mai vista dal 2005.
Ed anche in questo caso il global warming porta il freddo… mah, questione di media!
fonte dati , vedasi immagine allegata
Immagine allegata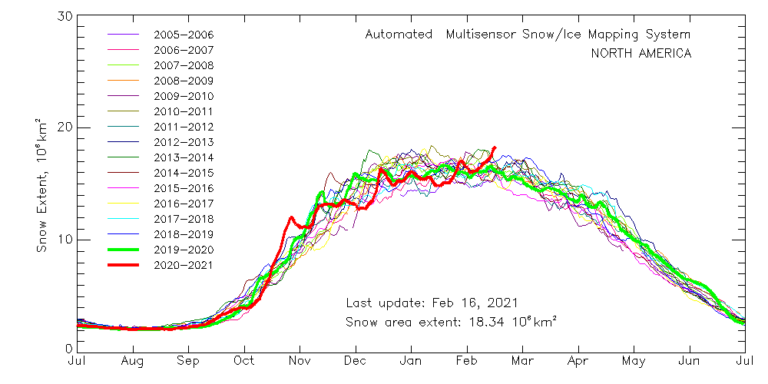
[…] TPI, un indice per IPO, l’oscillazione interdecennale del Pacifico — Climatemonitor […]