Finora ho fatto molti passi per verificare la presenza del massimo spettrale di 18.6 anni nelle serie climatiche, passi che sono sintetizzati nel sito lunar.html. Ora aggiungo altri due esempi.
Qualche giorno prima di ferragosto, occupandomi di altro, mi sono trovato nel sito di Harald Yndestad che presenta un articolo dal titolo “Lunar-driven Arctic Ice” in cui analizza una serie definita “Barents Sea Ice edge position”, con unità di misura “anni” e “gradi”. Assumendo che la posizione in gradi sia riferita a qualche estremo (ad esempio la latitudine del bordo più meridionale del ghiaccio) che nel lavoro non viene specificato (ma non ho trovato nulla anche negli articoli scientifici di Yndestad), questa serie fornisce indicazioni sull’avanzamento o arretramento della copertura ghiacciata del Mare di Barents, tra la Norvegia e le isole Svalbard.
L’autore analizza i dati con vari metodi offerti dalle wavelets (spettro di potenza, spettro di fase, spettro di autocorrelazione) e giunge alla conclusione che questi contengono la firma del ciclo lunare di 18.6 anni e delle sue armoniche 8D 9.3 a 93 anni).
Da quanto ho potuto dedurre dai suoi lavori scientifici, Yndestad non è famoso per fornire i valori numerici dei dati che usa o le indicazioni per ottenerli, così ho usato la figura 7 del suo blog per ricavare la posizione del bordo del ghiaccio nel Mare di Barents, dal 1579 al 2018, da cui ho calcolato lo spettro Lomb (la digitalizzazione implica quasi automaticamnte il passo variabile) di figura 1.

È notevole il fatto che questo spettro presenti marcate analogie con i periodi di abbondanza del merluzzo nell’Atlantico nord-orientale, trovati da Ottestad nel 1942 (v. sito di Yndestad) e con il livello del mare ad Aberdeen (Scozia nord-orientale, vedere qui su CM):
|
|
(*) In realtà non trovo un periodo di 57 o 55.8 anni ma due periodi vicini, di 49.7 e 64 anni la cui media è 56.85 anni.
Se l’interpretazione dei dati di posizione che ho dato più in alto è corretta, il fit parabolico del quadro superiore della figura ci dice che, in media, il bordo inferiore è salito di circa un grado di latitudine a partire dal 1760 circa, del tutto normale in un’ottica di recupero dalla PEG.
Lo spettro mostra una serie di massimi, tra cui anche 18.6 anni (non troppo in evidenza, per la verità) ma anche 11 anni (Sole), un paio di picchi con i periodi più elevati di El Nino (5.5 e 7.8 anni) e poi alcuni massimi su cui è opportuna una discussione: 9.8, 35.3, 55.8, 92, 120 anni possono essere assimilati a 9.3, 37.2, 56.85, 93, 111.6 anni, cioè le armoniche (/2; *2; *3; *5; *6) di 18.6 anni? Sembrerebbe di sì ma, ad esempio, mentre il risultato di Ottestad poteva facilmente implicare una minore risoluzione, tale da sostituire 57 anni a 49.7 e 64 anni, questo non dovrebbe essere vero per i dati di Aberdeen, più recenti.
Insomma, continuo a chiedermi se l’uso frequente di interpolazioni e smussamenti preventivi dei dati (per eliminare il rumore, si dice, ma quanto segnale c’è in quel “rumore”?) può amplificare massimi che normalmente verrebbero trascurati, tagliati via dall’uso dei livelli di confidenza? Comunque, a parte le considerazioni sulle armoniche, il massimo a 18.6 anni è presente in questi dati che vanno ad accrescere la lista delle serie climatiche in cui la Luna mostra la sua possibile influenza.
Il livello del mare a Brest (Francia)
Il “secondo passo” di questa breve camminata deriva da un lavoro di Mazzarella e Palumbo (1994) in cui si dimostra che vari parametri atmosferici (pioggia, temperatura, pressione, livello del mare) del Mediterraneo occidentale (Adriatico compreso) sono, o possono essere, condizionati dal ciclo nodale della Luna. Gli autori, tra le serie mareali usate, citano per la sua estensione temporale, quella di Brest (Francia Atlantica). Per verificare se la serie contiene segnali lunari contiene nel suo spettro, l’ho scaricata dal sito di PSMSL (1807-2018, con tre interruzioni) e la mostro in figura 2 insieme al suo spettro.
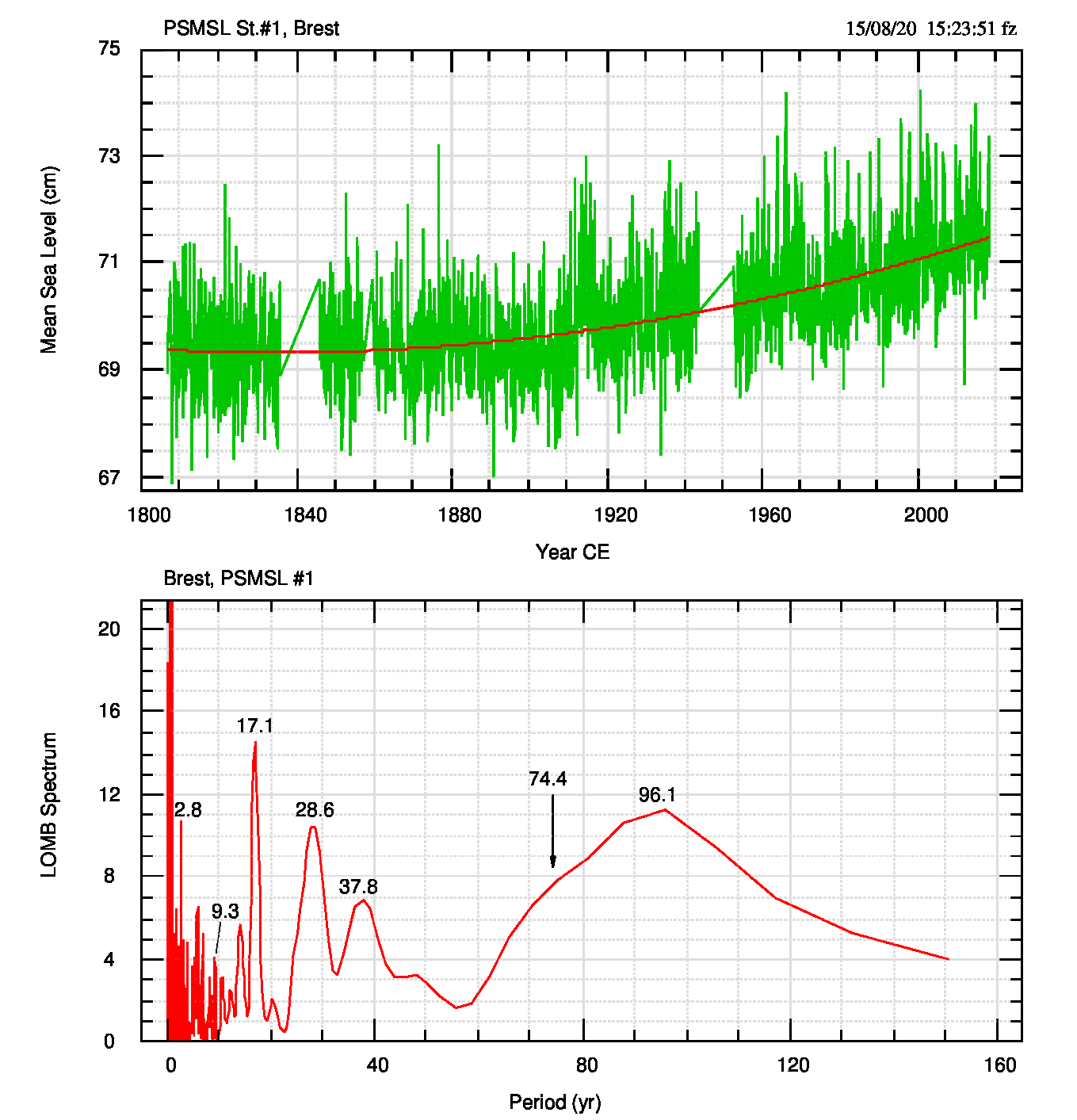
Lo spettro presenta segnali di alcune armoniche di 18.6 anni ma questo periodo non è presente, a meno di non volerlo rappresentato da 17.1 anni, massimo netto e potente. Le armoniche sono i massimi a 9.3, 37.2, e 96.1. Una “increspatura” nello spettro, a 74.4 anni, indicata dalla freccia, fa pensare alla 3.a armonica (18.6*4) ma è decisamente troppo vaga per qualsiasi considerazione.
In conclusione questo di Brest sembra un altro caso in cui il massimo di riferimento (l’armonica zero) manca, ma sono presenti le sue armoniche che dovrebbero, come nei lavori di Yasuda (2018) e di Serykh et al. (2019), relativi alla relazione Luna-El Nino, influenzare la forza e la durata di ENSO, senza la presenza del massimo più significativo. Questo aspetto continua a lasciarmi perplesso.
Ogni volta che avrò occasione di verificare la presenza del masssimo spettrale “lunare” di periodo 18.6 anni lo accetterò senza incertezze e allungherò la lista di casi di cui ho parlato all’inizio. Mi rendo conto, però, che esistono alcune certezze che non condivido, certo per mia ignoranza, e alcune forzature (come l’uso di periodi con 3-4 cifre decimali, derivati da dati incerti e/o pesantemente manipolati) che non voglio seguire.
Bibliografia
- A. Mazzarella, A. Palumbo: The Lunar Nodal Induced-Signal in Climatic and Oceanic Data over the Western Mediterranean Area and on its Bistable Phasing , Theor Appl Climatol, 50,93-102, 1994. https://doi.org/10.1007/bf00864906
- I.V. Serykh and A.G. Kostianoy: Seasonal and Interannual Variability of the Barents Sea Temperature , Ecologica Montenegrina, 25, 1-13,2019. https://doi.org/10.37828/em.2019.25.1
- Yasuda I.: Impact of the astronomical lunar 18.6-yr tidal cycle on El-Niño and Southern Oscillation, Scientific Reports, 8, 15206, 2018. doi:10.1038/s41598-018-33526-4
- Harald Yndestad, William R. Turrell, Vladimir Ozh Lunar nodal tide effects on variability of sea level, temperature, and salinity in the Faroe-Shetland Channel and the Barents Sea, Deep-Sea Research, I, 55, 10, 1201-1217, 2008. https://doi.org/10.1016/j.dsr.2008.06.003.
- Vedere anche il sito di Yndestad: https://www.climateclock.no/2019/11/01/itaque-mihi-non-satis-videmini (Barents Ice Edge position. Dati da figura 7).
Tutti i dati e i grafici sono disponibili nel sito di supporto


Avevo visto anche nell’ altro articolo in un altro dataset un errore di circa 1 anno sul ciclo dei 18,6 anni del ciclo lunare e mi domandavo se tale errore possa essere dovuto semplicemente alla sommatoria di differenze fra anno solare e anno civile.
Direi di no: se non ho capito male, qui per errore si intende la dispersione dei valori del nominale 18.6 anni attraverso i picchi dei vari dataset, diciamo tra 18 e 20 anni. La dispersione secondo me dipende dalla incertezza variabile da dataset a dataset e dalla precisione con cui si misurano (o si calcolano, dipende dai casi) le grandezze (temperatura, precipitazione, i diversi indici, SST,…). E’ questa (im)precisione che mi dice di cercare quel massimo nell’intervallo 18-20 anni: a volte mi sembra che il range (0.6-1.4 anni) che ho scelto sia troppo ampio, altre volte che vada bene, ma è sempre in funzione dei dati.
Ad esempio in mitra-etal-1991.pdf (fig.1) si considera la presenza del picco a 18.6 anni mentre in realtà si misura (si calcola come media) il valore di 17.4 anni.
Ho pensato alla dispersione perché non ho mai calcolato l’incertezza sui periodi che ricavo degli spettri e spero di aver fatto bene. Franco