L’evoluzione temporale delle piogge forti (i dati che tratto qui, nel database ECA sono definite heavy rain) è un indice della variazione del clima e ovviamente anche l’IPCC si occupa della questione. Ad esempio nel rapporto SR1.5 (presentato alla COP di Katowize, Polonia, nel 2018) al punto B1 si dice:
I modelli climatici prevedono forti differenze nelle caratteristiche dei climi regionali tra il riscaldamento globale odierno e quello di 1.5°C, e tra 1.5°C e 2°C. Queste differenze includono aumenti: nella temperatura media nella maggioranza delle regioni terrestri e oceaniche (alta confidenza), estremi di caldo nelle regioni più abitate (alta confidenza), pesanti precipitazioni in molte regioni (media confidenza) e la probabilità di siccità e mancanza di precipitazioni in alcune regioni (media confidenza)
Si deduce soltanto che si attendono (con media confidenza) nei prossimi decenni forti variazioni nel regime delle precipitazioni a causa dell’aumento di temperatura da quella attuale a +1.5°C e fino a +2°C (le “pesanti precipitazioni e la “mancanza di precipitazione” riportate nella stessa riga senza ulteriori dettagli, non portano chiarezza su quanto ci si deve attendere).
Dalla misura delle piogge (≥10mm in 24 ore) si ricava un indice climatico, definito R10mm, che elenca il numero di giorni con precipitazione maggiore o uguale a 10 mm nel corso dell’anno e nei due semestri caldo (AMJJAS) e freddo (ONDJFM). Questo indice è disponibile nel sito ECA&D e si riferisce alle 195 serie di precipitazioni giornaliere utilizzate per il database (Klein Tank et al., 2002). Di queste 195, “Respecting the data policies of the participants, a selection of the daily series in the ECA dataset (90%) is made available to the public”, cioè 118 serie di precipitazione (114 di temperatura) hanno i valori numerici disponibili.
Il database contiene temperature e precipitazioni giornaliere della Regione VI del WMO (Europa e Medio Oriente: Libano, Siria, Giordania e Israele) e pone particolare attenzione ai cambiamenti negli estremi giornalieri.
Anche se gli autori/gestori del database le definiscono “piogge pesanti”, da una discussione con Luigi Mariani è emerso che non lo sono e che per cercare la variazione delle piogge estreme si usano indici tipo R50mm, in particolare per le piogge alle nostre latitudini. Quindi è possibile considerare che l’indice sia generato da piogge normali e verificare se nel suo spettro si osserva il picco “lunare” (ciclo della linea dei nodi) a 18.6 anni in un intervallo di 18-20 anni.
Una sintesi di questa verifica è riportata in tabella 2 dove, di fianco al nome della stazione, il simbolo “§” indica per il semestre invernale la presenza del massimo a 18-20 anni e “~” ne indica la presenza appena oltre il limite dell’intervallo; per il semestre estivo, i due sinboli sono sostituiti da “#” e “^”, rispettivamente.
Dal database ECAD ho estratto il valore di R10mm per 28 stazioni: 24 europee, 2 israeliane e 2 ucraine, variamente distribuite in latitudine (da +65° a +31°), longitudine (da -22° a +45°) , altezza s.l.m. (da 1 a 1100 m) ed estensione temporale (da 13 a 206 anni).
L’elenco in ordine alfabetico delle stazioni è riportato in tabella 1, ma nel sito di supporto sono disponibili gli elenchi ordinati per latitudine (tabella 2) e per altezza s.l.m. (tabella 3)
Table 1: Stations ordered by Alphabetical Order. Look at ISO codes.
| N | STAID | Name | Nat. | Lat | Lon | Elev. |
|---|---|---|---|---|---|---|
| ECAD ID | Station | ISO | dd:mm:ss | ddd:mm:ss | m | |
| 01 | 00295 | aguiar | PT | +40:48:36 | -007:32:24 | 670 |
| 02 | 00271 | armagh | GB | +54:21:00 | -006:39:00 | 62 |
| 03 | 20416 | asarna | FI | +62:39:36 | +014:21:20 | 450 |
| 04 | 00335 | barcelona | SP | +41:25:05 | +002:07:26 | 412 |
| 05 | 00137 | beersheva | IL | +31:15:00 | +034:48:59 | 280 |
| 06 | 00169 | bologna | IT | +44:30:00 | +011:20:45 | 53 |
| 07 | 00162 | debilt | NL | +52:05:56 | +005:10:46 | 2 |
| 08 | 00121 | dublin | IR | +53:21:50 | -006:19:09 | 49 |
| 09 | 00170 | ferrara | IT | +44:49:57 | +011:37:15 | 15 |
| 10 | 00171 | genova | IT | +44:24:52 | +008:55:35 | 55 |
| 11 | 00147 | groningen | NL | +53:10:59 | +006:36:00 | 1 |
| 12 | 20415 | hanko | FI | +59:50:38 | +023:14:53 | 3 |
| 13 | 20335 | kauhava | FI | +63:08:08 | +023:03:10 | 44 |
| 14 | 00252 | kiev | UA | +50:24:00 | +030:31:59 | 13 |
| 15 | 20337 | malexander | SE | +58:04:18 | +015:14:09 | 197 |
| 16 | 00173 | milano | IT | +45:28:18 | +009:11:21 | 150 |
| 17 | 00254 | nikolaev | UA | +46:58:00 | +031:58:59 | 49 |
| 18 | 00274 | oxford | GB | +51:45:39 | -001:15:50 | 63 |
| 19 | 00291 | ponte de lima | PT | +41:46:12 | -008:35:24 | 15 |
| 20 | 00206 | poznan | PL | +52:11:58 | +018:39:37 | 115 |
| 21 | 07378 | savonlinna laukansaari |
FI | +61:47:44 | +028:50:57 | 94 |
| 22 | 20400 | skara | SE | +58:24:25 | +013:26:26 | 115 |
| 23 | 20454 | skien kjoer- bekksvingen |
NO | +59:10:36 | +009:37:46 | 9 |
| 24 | 00067 | stykkisholmur | IS | +65:04:26 | -022:44:00 | 13 |
| 25 | 00128 | tel aviv reading |
IL | +32:06:00 | +034:46:59 | 3 |
| 26 | 20282 | tianeti | GE | +42:06:00 | +044:58:00 | 1105 |
| 27 | 00305 | tranebjerg ost-1 |
DK | +55:49:59 | +010:37:00 | 18 |
| 28 | 00177 | verona villafranca |
IT | +45:22:59 | +010:52:00 | 68 |
Per ognuna delle stazioni è visibile nel sito di supporto il grafico con il fit lineare che mostra l’andamento medio della serie, sia per il semestre freddo (indicato con Winter) che per quello caldo (Summer). Il riassunto dei fit è nel file lfit.app
Non è possibile pubblicare tutti i grafici ma la composizione di figura 1 (pdf) mostra i due dataset più estesi (Bologna e Oxford) e i due più brevi (Asarna e Skien).
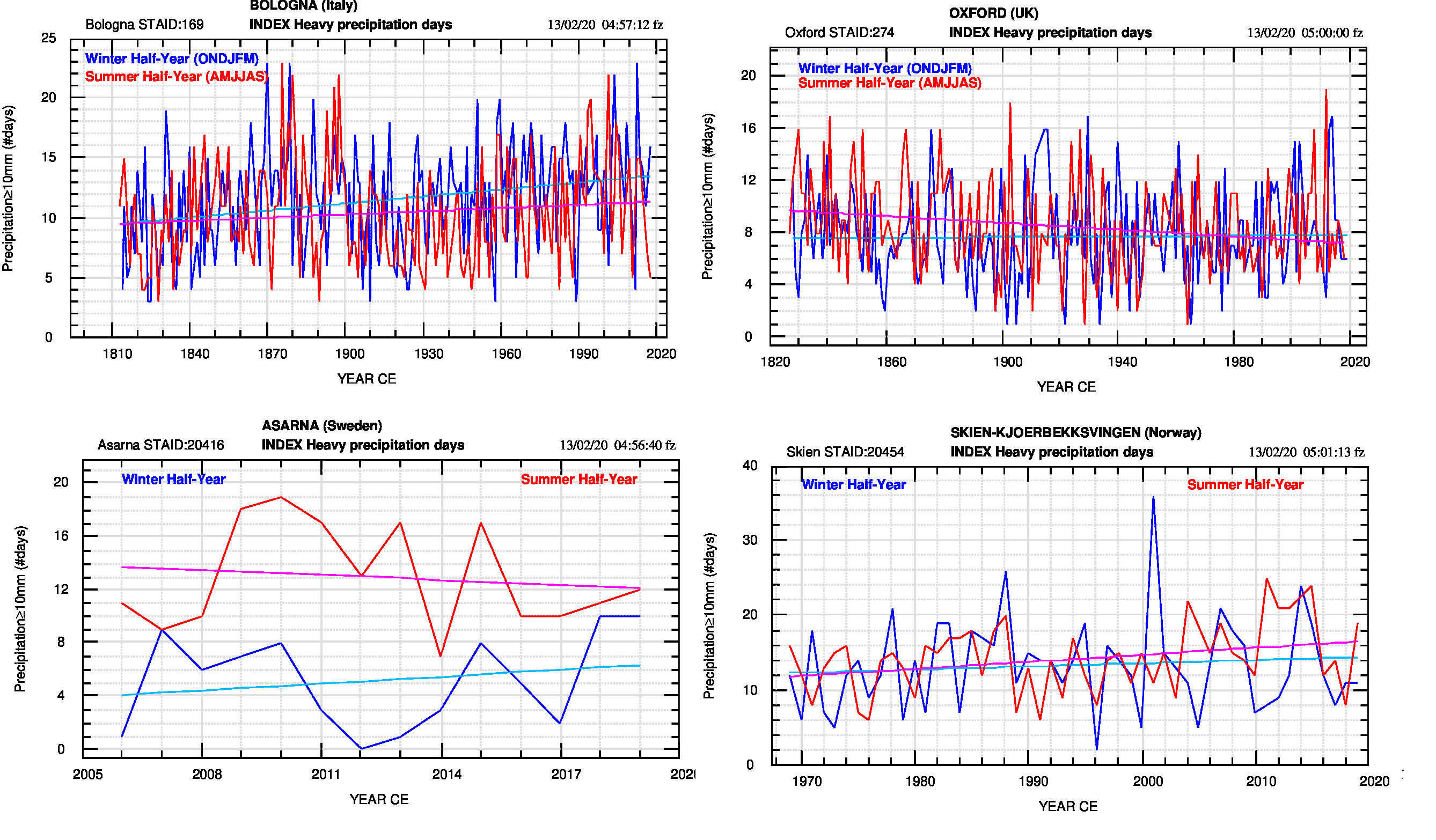
Anche da un sottoinsieme così limitato come quello di figura 1 si può intuire la diversità di comportamento e la dispersione dei valori di questo indice. L’insieme delle pendenze delle rette è riportato in tabella 2 e sintetizzato con i simboli + (retta crescente); – (retta decrescente); = (retta che non varia in pendenza); ~= (retta con variazione minima, quasi nulla), porta ad un complessivo di 10(+), 6(-), 9(~=), 2(=) per il semestre caldo e di 14(+), 6(-), 6(~=), 1(=) per quello freddo, e quindi ad una preponderanza della tendenza all’aumento del numero di giorni con pioggia ≥10 mm in entrambi i semestri, anche se le 11 pendenze invariate del semestre caldo e le 7 del semestre freddo non devono essere trascurate, così come non è trascurabile la forte dispersione dei dati osservati.
Table 2: Stations ordered by Alphabetical Order with rise(+)/drop(-) of R10mm.
Look at ISO codes. For Winter, “§” outlines a 18-20 year spectral maximum, while “~”
indicates that the maximum is less evident. The same for Summer , where “#” and
“^” are the symbols used.
|
Note:~= includes
|
* shortest series (13 years); **longest series (206 years). ? Spectrum unclear: not used.
Invito a verificare nei grafici originali che le pendenze delle rette di regressione di R10mm per le singole stazioni sono molto basse, del tipo 2-5 giorni su 120-150 anni, con punte di 2-3 giorni su 60-70 anni e, a fronte di una forte dispersione dei valori annuali, appaiono poco significative. Per questo mi limito a fornire il segno della pendenza e a descrivere il comportamento delle stazioni nel loro complesso.
Comportamenti complessivi
Sono il modo di comportarsi di tutte le stazioni rispetto alla latitudine e all’altezza s.l.m.
Nell’analisi di queste situazioni non è stata considerata la stazione di Asarna (FI) a causa della sua eccessiva brevità (13 anni).
In figura 2 sono presentate le pendenze, con le stazioni ordinate rispetto alla latitudine, di entrambi i semestri. Lungo l’intervallo di latitudine o rispetto al numero d’ordine della stazione (da 1 a 27) si osserva una diminuzione di poco più di 2 giorni su poco meno di 34°.
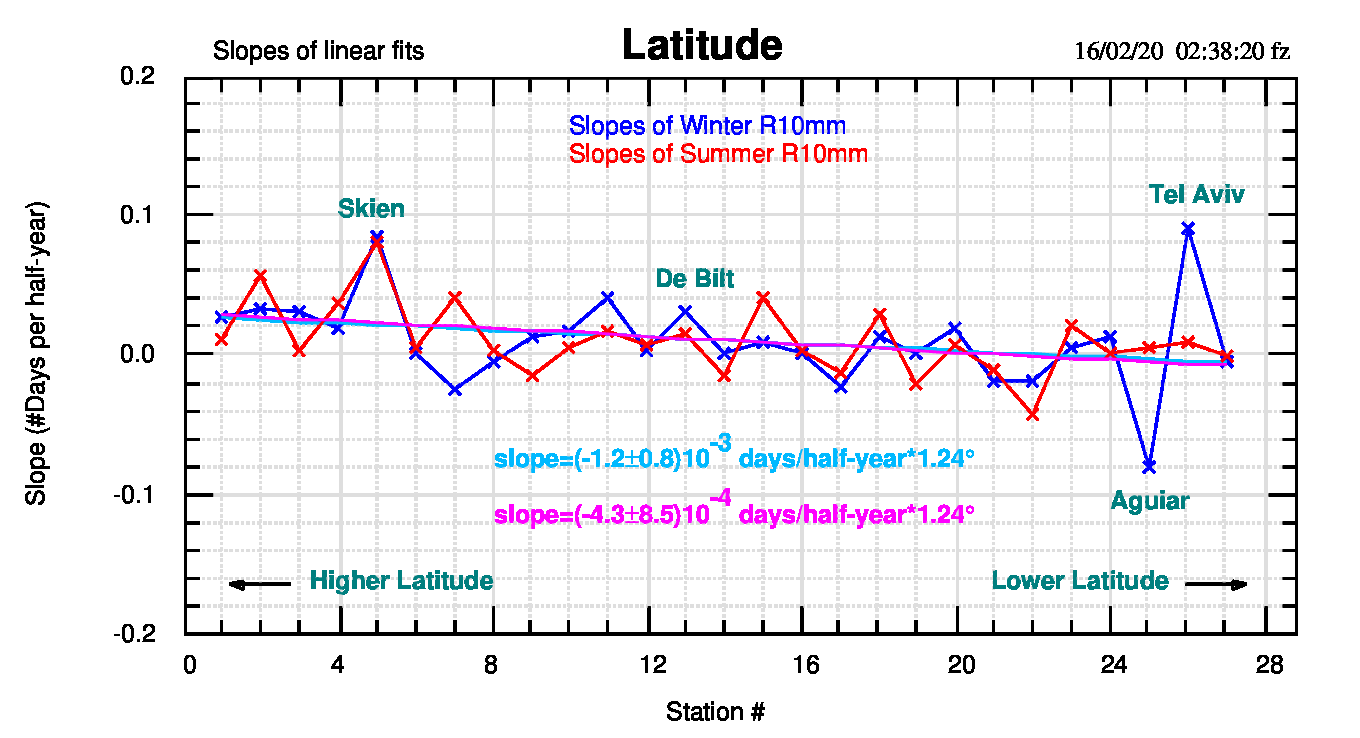
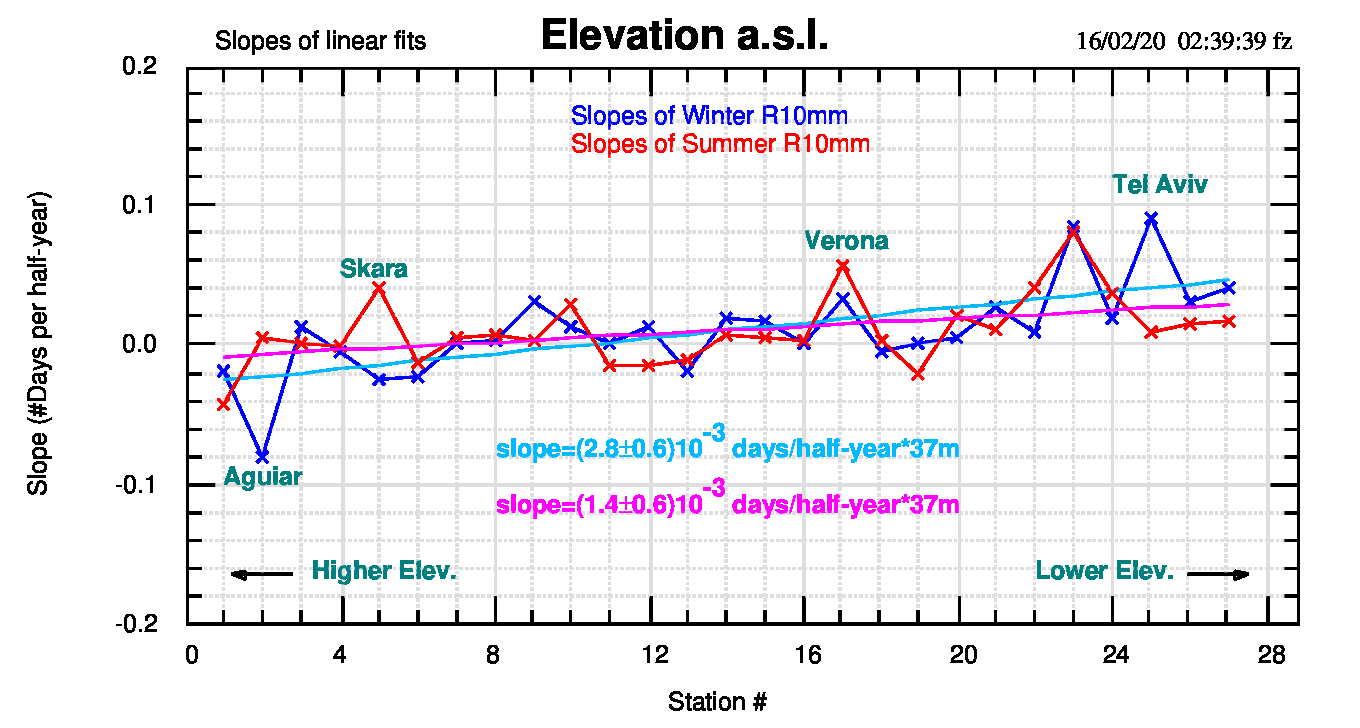
Rispetto all’altezza s.l.m. si osserva che le stazioni più basse mostrano pendenze più elevate (cioè un aumento nel tempo di R10mm) rispetto alle stazioni più in quota, come mostrato in figura 3. Da notare la bassa dispersione delle pendenze, in entrambi i casi, con Aguiar e Tel Aviv casi estremi del periodo freddo e Skara e Verona estremi del periodo caldo.
Massimo spettrale a 18.6 anni
In precedenza avevo trattato l’esistenza e la validità del massimo spettrale a 18.6 anni (ciclo nodale della Luna) e, non pubblicato, nella copertura nuvolosa media della regione “Low” (esempio) del database austriaco Histalp quando le piogge delle stazioni nella stessa regione non mostrano la presenza del massimo a 18-20 anni.
- in un indice legato alle piogge argentine (qui)
- nelle piogge lungo i bacini di 15 fiumi inglesi (qui),
- lungo il bacino del Po dall’800 al 2019 (qui)
In questa sezione tento di verificare se lo stesso massimo spettrale è presente anche nell’indice R10mm e calcolo lo spettro Lomb (il passo non è necessariamente costante, per la presenza di dati mancanti) delle 28 stazioni, sia per il semestre invernale (ottobre-marzo) che per quello estivo (aprile-settembre). Come esempi mostro lo spettro di Bologna e Asarna combinati nella stessa figura per il semestre invernale (pdf) e per quello estivo (pdf).
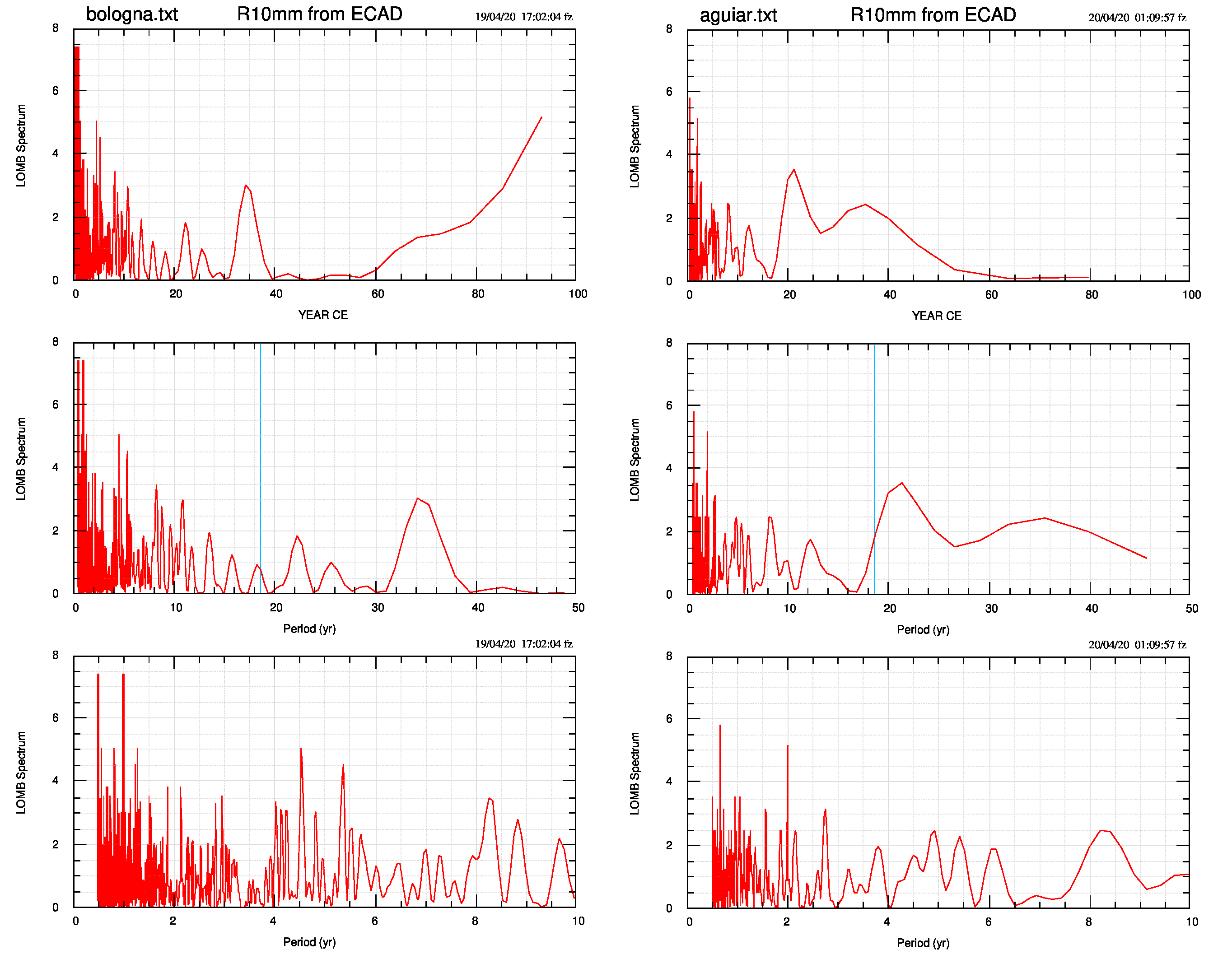
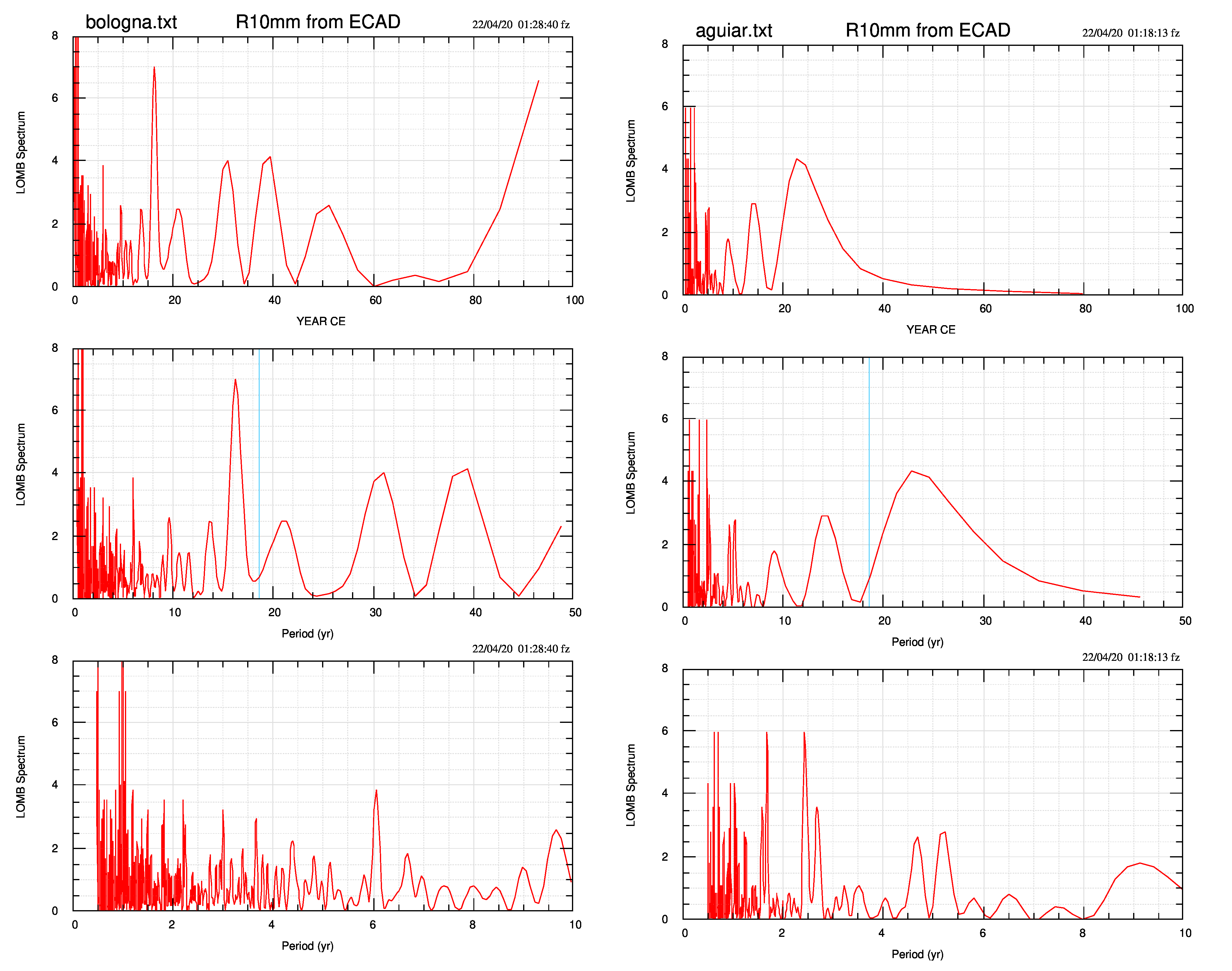
In generale, 16 su 27 stazioni (59%) mostrano per il semestre invernale il massimo a 18-20 anni, mentre per il semestre estivo le stazioni sono 17/27 (63%).Il risultato è identificato in tabella 2, per il semestre invernale, dal simbolo § quando il massimo è presente e dal simbolo ~ quando è più incerto, e per il semestre estivo dai corrispondenti simboli # e ^, e descritto come:
- 24/27 stazioni (89%) mostrano un massimo in estate o in inverno.
- 10/27 stazioni (37%) mostrano un massimo sia in estate che in inverno.
- rispetto alla latitudine λ, in inverno 0/5 stazioni a λ≥59°50′ e 16/22 stazioni (73%) con λ≤ 58°24′ mostrano il massimo a 18-20 anni. In estate il massimo è presente in 2/5 stazioni con λ≥59°50′ e in 15/22 stazioni (68%) con λ≤ 58°24′.
- non sembra esserci una relazione tra il massimo e l’altezza s.l.m. delle stazioni, sia in estate che in inverno; la presenza del massimo è distribuita su tutto l’intervallo delle altezze.
Conclusioni
Anche se le piogge considerate in questo articolo non costituiscono un insieme di valori estremi, possiamo ugualmente dedurre alcune informazioni dall’indice R10mm:
- La sua pendenza in funzione del tempo varia quasi casualmente nel periodo estivo (semestre estivo: AMGLAS) con 10 pendenze positive (+), 6 negative (-), 9 quasi nulle (~=) e 2 nulle (=). In inverno (semestre invernale: ONDGFM) la situazione è più netta, con 14(+), 6(-), 6(~=), 1(=).
- Complessivamente si può dire che la tendenza è all’aumento del numero di giorni, in un anno, con precipitazioni maggiori o uguali a 10 mm nelle 24 ore. La tendenza è meno chiara in estate e più netta in inverno.
- Si osserva anche una debole tendenza alla diminuzione di R10mm al crescere della latitudine geografica (figura 2) e ad un suo aumento in funzione dell’altezza s.l.m. delle stazioni (figura 3).
- In relazione alla presenza nello spettro di R10mm del massimo a 18.6 anni (ciclo della linea dei nodi della Luna), che qui ho considerato nell’intervallo 18-20 anni, si può dire che il 37% delle stazioni mostra la sua presenza in entrambi i semestri e che quasi il 90% delle stazioni lo mostra in un semestre o nell’altro (il 59% in inverno e il 63% in estate). Quello presentato qui è quindi un altro caso in cui, nelle piogge o nei loro derivati, si manifesta la “firma” lunare osservata per la prima volta, a quanto mi risulta, da Agosta (2014) nelle piogge argentine dell’area sub-andina.
Bibliografia
- Eduardo Andres Agosta: The 18.6-year nodal tidal cycle and the bi-decadal precipitation oscillation over the plains to the east of subtropical Andes, South America, Int. J. Climatol., 34, 1606-1614, 2014. https://doi.org/10.1002//joc.3787
- Klein Tank, A.M.G. and 38 Coauthors, 2002.Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment., Int. J. of Climatol., 22, 1441-1453. https://doi.org/10.1002/joc.773
| Tutti i grafici e i dati, iniziali e derivati, relativi a questo post si trovano nel sito di supporto |


Caro Zavatti,
Voglio tolgiere di mezzo l’ambiguità in cui sono caduto nel confonde due cicli lunari di natura differente ma simili nella durata di poco più di 18 anni: il ciclo nodale e il saros.
“Because the orbital plane of the Moon precesses in space, the lunar nodes also precess around the ecliptic, completing one revolution (called a draconic or nodal period) in 18.612958 years (6,798.383 days). (This is not the same length as a saros.)” (https://en.wikipedia.org/wiki/Lunar_node)
Il saros (https://en.wikipedia.org/wiki/Saros_(astronomy)) è il periodo che impiega la luna per riportarsi circa alla stessa posizione iniziale. Il periodo che impiega la luna per girare intorno alla terra e trovarsi nel medesimo allineamento fra questa e il Sole (mese sinodico) essendo pari a 29.5306 giorni, dopo 223 rivoluzioni sinodiche la luna ritorna allo stesso punto: 223*29.5306=6585.3223 (cioè 18 anni, 11 giorni e 8 ore). Fu questo il ciclo identificato da Toaldo come responsabile dei tempi di ritorno di certi fenomeni meteorologici:
“Questi periodi altro non sono, che un Ciclo di 223. Lune corrispondente a giorni 6585. ed un terzo; che gli piacque di nominare Saros, perchè così appunto gli Astronomi Caldei chiamarono quel periodo di 18 anni, che indica il ritorno dell’Ecclissi, che fa girare in serie tutti i punti della Luna con tutte le disuguaglianze della medesima”
“Non dubitando egli che … questo Pianeta non abbia qualche influenza sull’ammosfera, e sulle Stagioni, s’avvisò che a ragione gli dovesse essere concesso, che quella rivoluzione, che riconduce i Punti Lunari, dovesse altresì ricondurre un circolo d’impressioni simili nell’aria, cioè un ritorno di tempi, e di stagioni”
“Conobbe la necessità di confermare quest’argomento d’induzione coll’esperienza, ed avendo una serie d’Osservazioni Meteorologiche proprie dei due Poleni Padre, e Figlio, e del Morgagni che abbracciavano lo spazio di 57. anni, cioè dal 1725. al 1781, potè formare una tavola di tre Saros, e più, pubblicata l’anno stesso 1781. in Francese, ed in Italiano dimostrante un ritorno di tempi, di piogge, di venti, di nebbie, di tempeste ec. ritorno non già d’eguaglianza numerica, che sarebbe chimerico il pretenderlo, ma di una tal quale rassomiglianza, bastante però a dare una valevole prova dell’Influenza Lunare”
Confido nelle sue preziose analisi e nelle prossime considerazioni di Donato per sciogliere questa ambiguità e svelare l’influenza dei cicli lunari sul nostro pianeta.
Con stima,
Gianni
Caro Gianni,
grazie per aver voluto sottolineare l’ambiguità insita nei due periodi di “influenza lunare”. Di mestiere facevo l’astronomo e sono ben consapevole della possibilità di prendere uno dei periodi per l’altro. Ma sono anche consapevole del fatto che i dati meteo-climatici, a differenza di quanto penso sia successo per i Poleni e Morgagni degli albori, sono molto spesso trattati matematicamente con omogenizzazioni, somme, medie, eliminazione di estremi, ricostruzione di dati mancanti, ecc. e ho poca speranza di riuscire a distinguere tra 18.6 e 18 anni. In effetti ho alcuni
massimi di 18 anni ma non ho un criterio per distinguere uno dall’altro. Come ho scritto nel post sull’atollo di Palmyra, non sono in grado di calcolare
l’errore nel posizionamento del periodo di un massimo spettrale, per cui un confronto è difficile. Pensandoci meglio, non mi sembra di aver mai trovato due picchi attorno a 18 anni insieme, anche se non ne sono sicuro. Penso che l’unica cosa che sia possibile fare è ridurre l’intervallo da 18-20 anni a 18-19 anni o giù di lì. Un caro saluto. Franco
Caro Franco,
dopo tutti i dati che stai pubblicando comincio a pensare che il ciclo lunare di 18.6 anni ha influenza sul clima terrestre. Molto interessante mi è parsa, in particolare, la citazione fatta da Gianni dell’articolo di Giuliacci che chiarisce in modo piuttosto convincente, le basi fisiche dell’interazione Terra-Luna relativamente alle vicende climatica del nostro pianeta.
.
Proprio in questi giorni un gruppo di ricerca italiano ha pubblicato un interessante articolo che riguarda il ciclo di 18,6 anni e quello di 8,8 anni sulle deformazioni della crosta terrestre. Sto scrivendo qualche considerazione in merito, per cui ne parleremo a breve. Già tre o quattro anni fa mi entusiasmai, ma le critiche all’ipotesi che la Luna potesse influenzare la crosta terrestre mi smontarono. Questa volta sarò più tenace. 🙂
.
Questo benedetto ciclo lunare che all’inizio mi lasciava piuttosto scettico, sta cominciando ad appassionarmi.
Ciao, Donato.
Caro Donato,
dopo aver spedito la risposta a Gianni, ho passato in rassegna tutti i post che ho pubblicato (nei prossimi giorni farò la stessa cosa per quelli non pubblicati) e ho trovato un massimo spettrale tra 18 e 20 anni in almeno 15 situazioni climatiche, incluse quelle già citate; dalla salinità nel Canale Faroe-Shetland alle piogge nel Sahel, al livello marino di Aberdeen in Scozia, al livello minimo del Nilo, al TPW (Total Precipitable Water tra +- 60°), al
livello del mare a Stoccolma, a quello di Suva nelle Isole Fiji; dalle coordinate x,y del Polo nord ad un caso dell’indice CEI (indice degli eventi estremi) relativo alla parte ovest degli USA.
Attenderò con molta curiosità le tue considerazioni sul lavoro del gruppo italiano che citi.
Io avevo sempre trascurato questo massimo spettrale, e magari ho partecipato alle critiche nei tuoi confronti anche se non lo ricordo, fino a che non ho letto il lavoro di Eduardo Agosta e ho cominciato a cercarlo in altre
realtà. L’unico posto dove non lo trovo (almeno non direttamente) è nelle serie di El Nino e anche in una serie di d18O dai coralli dell’atollo di Palmyra, un buon proxy per ENSO, il cui post ho già spedito a Guido. Ciao. Franco
Caro professor Zavatti,
Accolgo con piacere questo ulteriore contributo riguardo all’impronta lunare sul clima terrestre.
Si tratta di studi importanti se è vero che valsero a Giuseppe Toaldo, che li inizio’ nel 18° secolo, il titolo di fondatore della moderna scienza meteorologica: “Quest’esempio ebbe seguaci a Bade, ed all’Haya, e risultò in gloria del Toaldo quel che fu pubblicato da queste Novelle Società, che comprovando gl’Influssi Lunari, e que’ periodi detti già dal nome di lui Toaldini, non dubitarono di dare al medesimo il glorioso titolo di Riformatore, o più tosto Creatore della vera Scienza Meteorologica” (https://it.wikisource.org/wiki/Completa_raccolta_di_opuscoli_osservazioni_e_notizie_diverse_contenute_nei_giornali_astro-meteorologici/Elogio_di_Giuseppe_Toaldo)
Ho recuperato un estratto (che riporto sotto) del libro di Mario Giuliacci “Se non ci fosse la luna”, del 1997 (https://www.ibs.it/se-non-ci-fosse-luna-libro-mario-giuliacci/e/9788842521600#), in cui si rimanda agli studi degli anni ’60 dei meteorologi russi Maksimov e Smirnov riguardo l’influenza del ciclo lunare di circa 18.6 anni sul posizionamento dell’anticiclone delle Azzorre in Atlantico (i riferimenti sono in fondo al commento insieme ad altri più recenti contributi).
Buona lettura e a presto per nuovi approfondimenti.
“Il ciclo di 18 anni nell’inclinazione dell’orbita lunare sarebbe anche responsabile di una periodica oscillazione del livello degli oceani. E’ questa la conclusione a cui sono giunti nel 1965 due climatologi russi, Maksimov e Smirnov, i quali hanno accertato che quando la luna si spinge verso la massima declinazione di 28°, il Medio Atlantico tende a sollevarsi di quasi 13 cm rispetto alla posizione di minima declinazione di 18° raggiunta circa 9 anni dopo. Il dislivello che in tal modo si viene a creare tra la superficie della fascia oceanica compresa tra i 30° ed i 40° di latitudine e quella posta a più alte latitudini sposta, sotto la spinta della gravità, enormi quantità d’acqua verso le calotte polari, le cui acque superficiali pertanto si riscaldano mediamente di 0.2°/0.4°, provocando una parziale fusione dei ghiacci polari … Queste modificazioni fisiche dell’ambiente artico, sebbene di lieve entità, potrebbero essere fonte di temporanee anomalie nella circolazione generale dell’atmosfera a scala planetaria … ed in effetti un comportamento analogo è stato riscontrato anche negli anticicloni che occupano in permanenza la fascia fra i 25° ed i 45° di latitudine -la più esposta alle periodiche incursioni della luna- e dei quali è insigne e famoso membro anche l’anticiclone delle Azzorre. In particolare, man mano che l’orbita lunare si avvicina alla latitudine-limite di 28°, l’aumento della forza di attrazione fa scendere al di sotto dei valori medi la pressione al suolo alle medie latitudini, cosicché l’AA viene sospinto e relegato verso le zone tropicali, agevolando in tal modo l’ingresso delle perturbazioni atlantiche sull’area euro-mediterranea. Quando invece la luna, dopo quasi 9 anni, si porta nella posizione di minima declinazione, l’AA tende a spostarsi verso latitudini più alte di quelle di solito occupate, ossia più su delle Isole Azzorre. In tal modo le perturbazioni che si originano sul Nordatlantico, nel loro movimento verso E, sono costrette a seguire traiettorie più settentrionali e nello stesso tempo diviene meno frequente la loro presenza nell’area subtropicale” (Giugliacci, 1997).
Maksimov, I.V., Smirnov, N.P., 1965. A contribution to the study of causes of long – period variations in the activity of the Gulf Stream. Oceanology 5, 15-24.
Maksimov, I.V., Smirnov, N.P., 1967. A long – term circumpolar tide and its significance for the circulation of ocean and atmosphere. Oceanology 7, 173-178.
Royer, T.C., 1993, High-latitude oceanic variability associated with the 18.6-year nodal tide. Journal of Geophysical Research 98, 4639-4644 (https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/92JC02750)
Yndestad, H., 2006. The influence of the lunar nodal cycle on Arctic climate. ICES Journal of Marine Science 63, 401-420. (https://academic.oup.com/icesjms/article/63/3/401/718604)
Yndestad, H., Turrell, B., Ozhigin, V., 2008. Lunar nodal tide effects on variability of sea level, temperature, and salinity in the Faroe-Shetland Channel and the Barents Sea. Oceanographic Research Papers 55, 1201-1217 (https://www.researchgate.net/publication/248505992_Lunar_nodal_tide_effects_on_variability_of_sea_level_temperature_and_salinity_in_the_Faroe-Shetland_Channel_and_the_Barents_Sea)
Humlum, O., Solheim, J-E., Stordahl, K., 2012. Spectral analysis of the Svalbard temperature record 1912–2010. Advances in Meteorology 2011: 175296. (https://www.hindawi.com/journals/amete/2011/175296)
Caro Gianni,
devo dire, e con piacere, che la colpa di questi contributi è esclusivamente sua, a partire dall’informazione sul lavoro di Agosta (2014) che ha acceso una lucina nella mia testa. E per questa “colpa” la ringrazio.
Intanto, ieri ho acquisito un’ulteriore informazione, che avevo già ma che non avevo considerato: raccogliendo in un unico posto una serie di dati sugli eventi estremi che avevo pubblicato in precedenza su CM, ho ritrovato
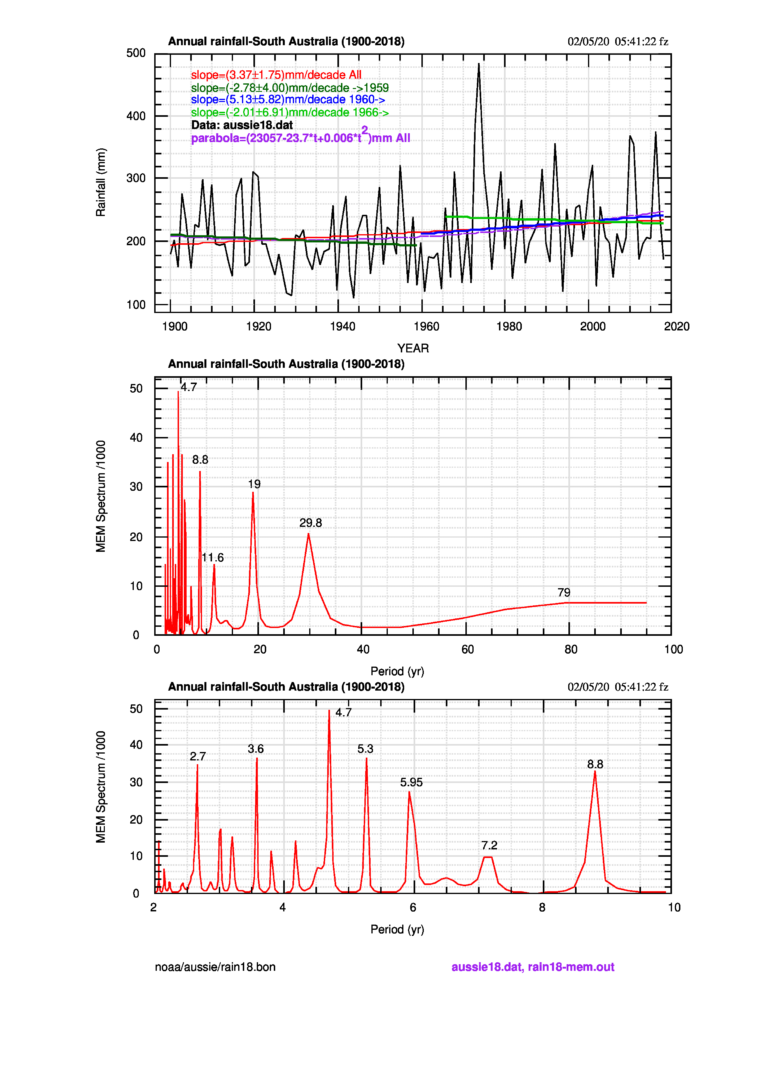
lo spettro di piogge annuali in Australia meridionale che presenta un netto massimo a 19 anni (accludo in fondo l’immagine). Quindi adesso, a questo elenco che contiene i casi nei quali trovo il picco a 18-20 anni, ho aggiunto
le piogge australiane alle piogge argentine, alle piogge inglesi in molti bacini fluviali, alle piogge nel bacino del Po, alla copertura nuvolosa nel database Histalp (in particolare la regione “Low”, ma non nelle piogge delle
stesse stazioni) e all’R10mm, e la faccenda sta diventando interessante.
Ho anche ricevuto un commento da parte di Ilya Serykh, il cui lavoro ho citato nel post sul picco di 18.6 anni (http://www.climatemonitor.it/?p=52692), e sempre per merito suo, che conferma il modello che usa (SNA o strange nonchaotic attractor) e i massimi spettrali che dovrebbero essere le armoniche di 18.6, 1.17 (Chandler wobble) e 11 anni. Il suo commento apre nuove prospettive, anche se io capisco male perché nello spettro di ONI (Oceanic Nino Index) dovrebbero esserci solo le (sub-)armoniche e mai il picco principale che
trovo solo nelle piogge.
Comunque, grazie per le referenze e per il pezzo tratto da Giuliacci che ho letto con interesse. Franco
Immagine allegata