In questo post parlo di DMI (Dipole Mode Indian Index), detto anche IOD (Indian Ocean Dipole, Sahu et al.,2010), di TNA (Tropical Northern Atlantic Index) e TSA (Tropical Southern Atlantic Index), estratti da una ben più vasta famiglia di indici oceanici: ad esempio SAD -South Atlantic Dipole- o AEM -Atlantic equatorial mode- o ancora SWSA -South Western South Atlantic- come centro debole e forse inesistente di AEM (Kayano et al., 2013), oltre ai più noti NAO, AMO, PDO, AO, SAM ed altri, tutti connessi con vari modi di oscillazione degli oceani (Kayano et al., 2013, Enfield et al., 1999, Hu e Fedorov, 2019) e correlati più o meno bene con El Nino/La Nina (ENSO) che è il più importante modo di oscillazione (non periodico) dell’Oceano Pacifico.
Le definizioni di questi indici sono (v. ad esempio ESRL-NOAA):
- DMI/IOD: gradiente zonale anomalo attraverso l’Oceano Indiano equatoriale. Differenza tra l’anomalia di SST (temperatura marina superficiale) in due aree, ad occidente e ad oriente dell’India (mappa).
- TNA: Anomalia della media della SST mensile in un’area atlantica subito a nord dell’equatore (mappa)
- TSA: Anomalia della media della SST mensile in un’area atlantica subito a sud dell’equatore (mappa)
Sono indici che appaiono, almeno in maniera vaga, “circondare” ad est e ad ovest la zona del Pacifico dove si sviluppa ENSO. Sono quindi adatti ad osservare le relazioni che possono insorgere tra modi diversi di oscillazione oceanica.
DMI
DMI/IOD ed ENSO dominano la variabilità climatica dei paesi che si affacciano sugli oceani Indiano e Pacifico tropicali, rispettivamente. Diversi studi hanno mostrato che eventi IOD hanno forte influenza sul clima di Asia e Africa orientali e Indonesia; sul monsone indiano, Australia, Brasile, e regione mediterranea (Sahu et al., 2010 e loro bibliografia) ed è stato dimostrato che gli incendi boschivi del cosiddetto “sabato nero” nella regione di Victoria (Australia) del febbraio 2009 sono stati causati dal valore positivo di IOD che, peraltro, si trova stabilmente in questa fase dal 1960-61 come si vede in figura 1 (pdf).
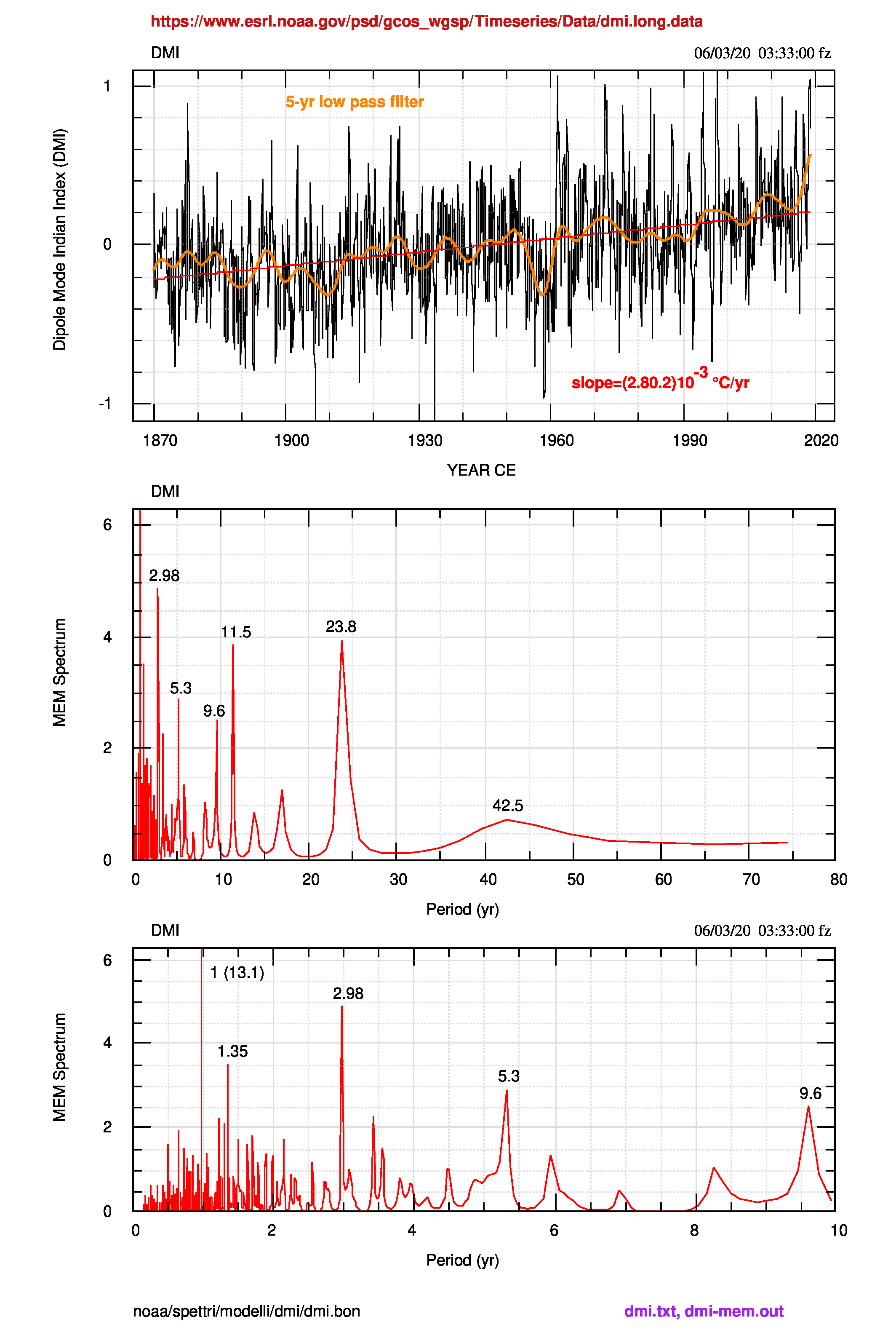
IOD è normalmente caratterizzato da raffreddamento anomalo delle SST dell’oceano Indiano equatoriale sud orientale e riscaldamento anomalo dell’oceano Indiano equatoriale occidentale.
IOD sembra essere accoppiato all’atmosfera (in particolare alla pressione e ai conseguenti venti) e indipendente da ENSO: “The spatio-temporal links between sea surface temperatures and winds reveal a strong coupling through the precipitation ®eld and ocean dynamics. This air±sea interaction process is unique and inherent in the Indian Ocean, and is shown to be independent of the El Nino/Southern Oscillation” (Saji et al., 1999)
TNA e TSA
Queste regioni potrebbero in qualche modo essere accoppiate, anch’esse a dare origine a un dipolo (parte positiva a nord e negativa a sud, o viceversa) come DMI, ma l’analisi statistica di Enfield et al., 1999 (sezione 4) esclude questa eventualità. Allo stesso risultato sembra condurre la funzione di cross-correlazione tra le due serie, come si vede in figura 2.
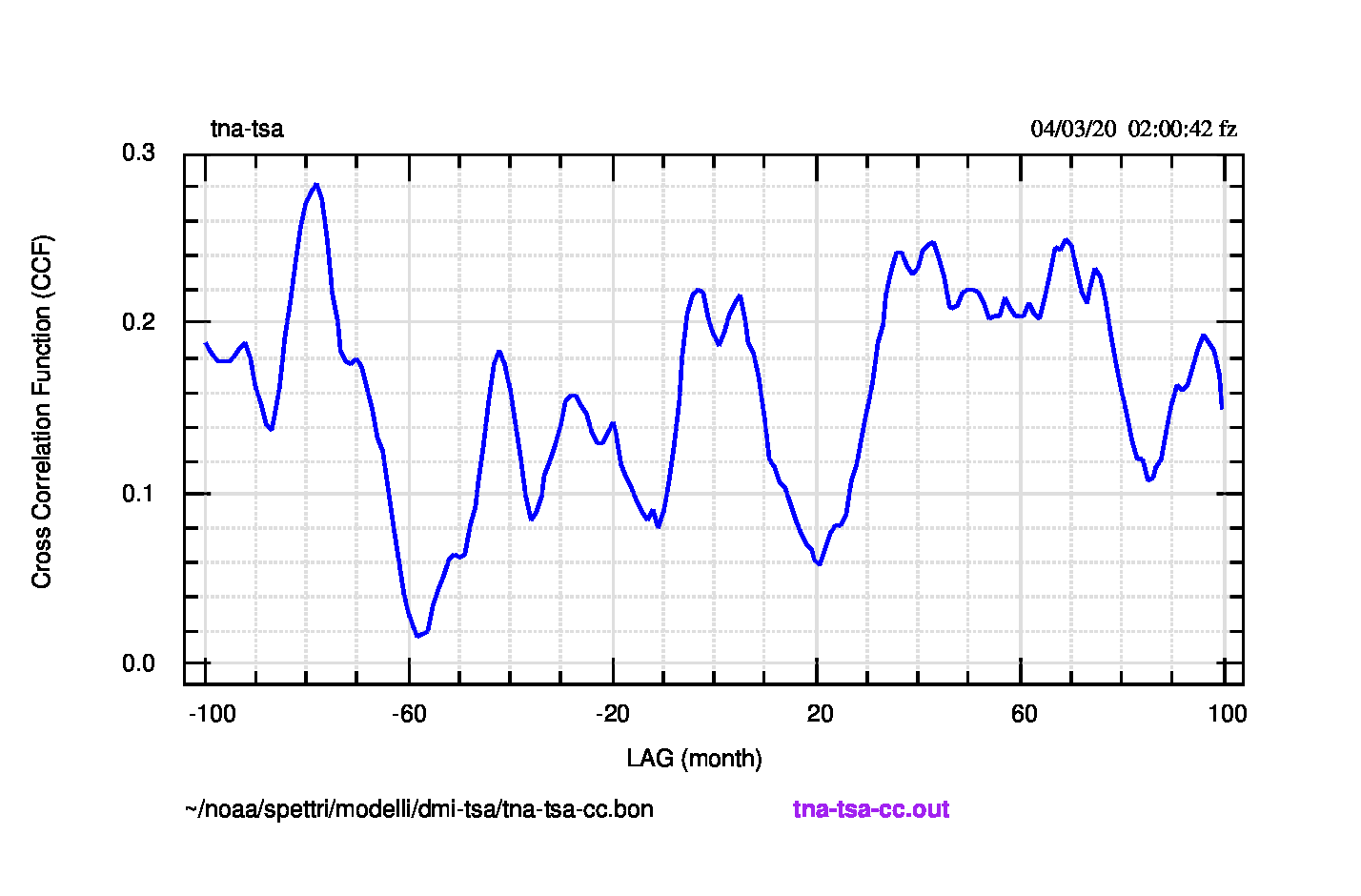
“Both regions (cioè TNA e TSA) show large peaks in the 10- to 12-year band, but only the TNA energy continues to rise in the multidecadal band (40- 60 years)” (Enfield et al., 1999). La frase descrive bene anche la situazione di venti anni dopo, come si vede dal confronto tra gli spettri di TNA e TSA delle figure 3 (pdf) e 4 (pdf) successive.
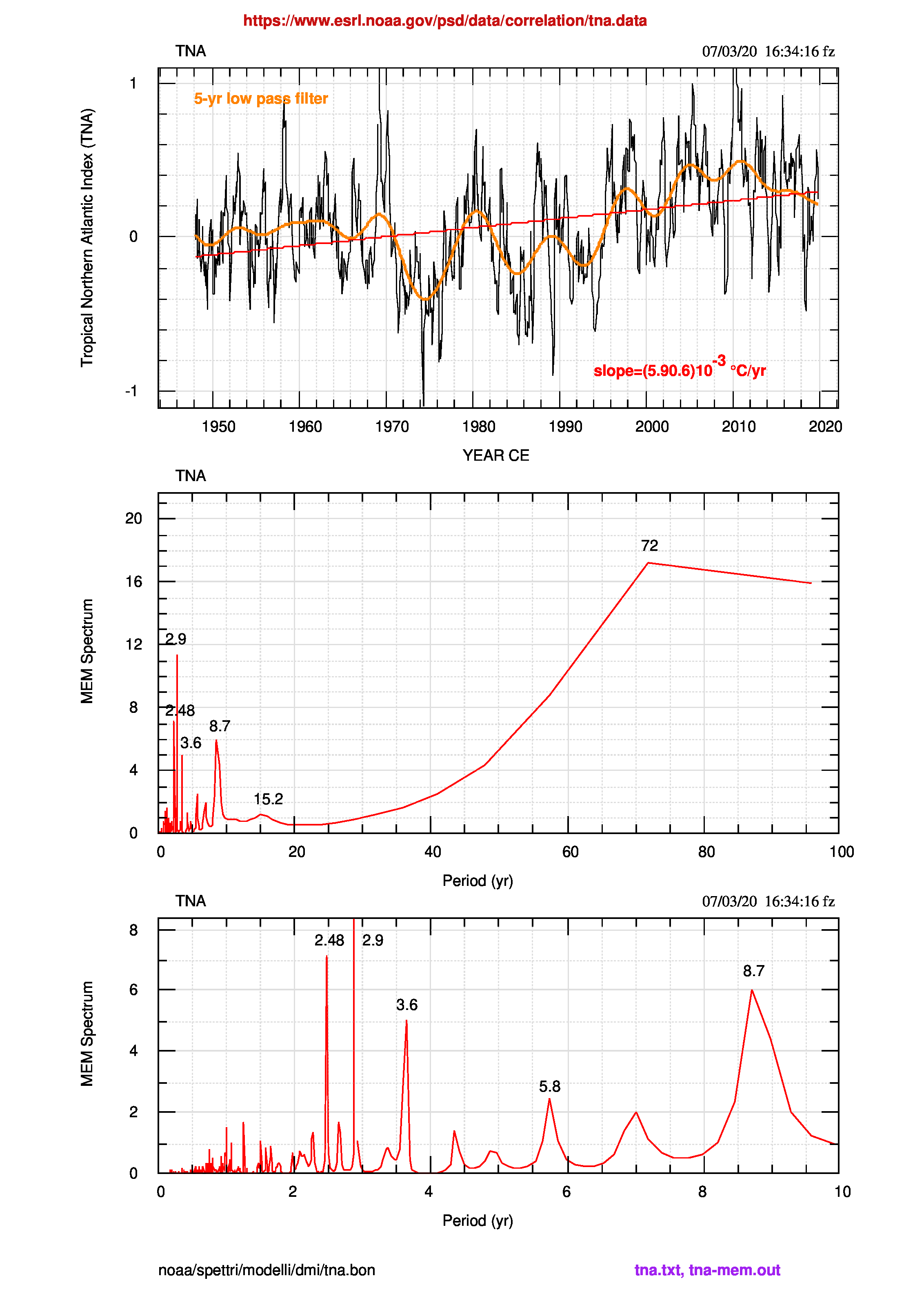
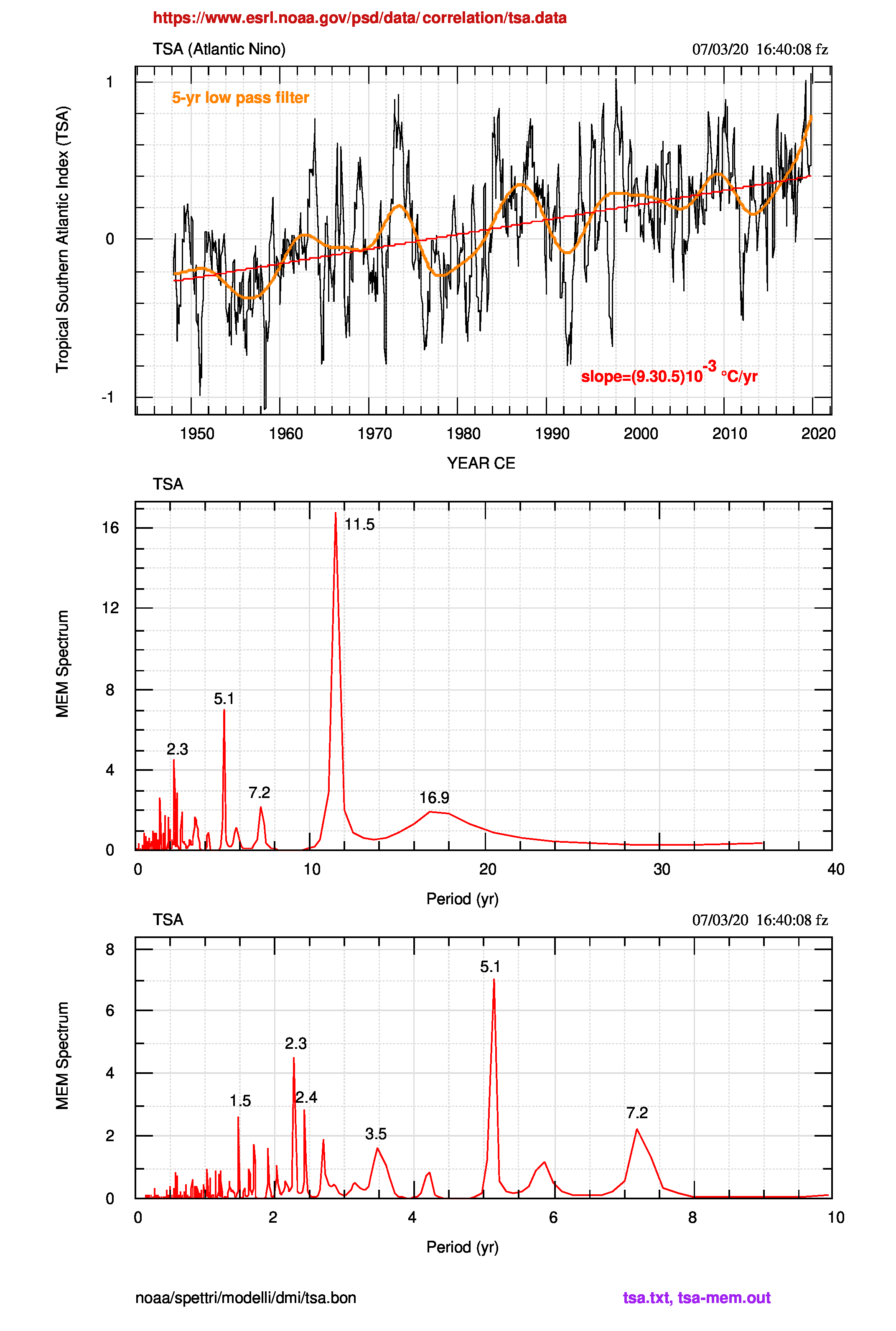
Il test di Student sulle pendenze dei fit lineari mostra che le pendenze non sono statisticamente compatibili.
“The lack of a similar reduction for TSA is consistent with observations of a stronger ENSO connection in the North Atlantic” (Enfield et al, 1999): questa frase sembra essere confermata dalla tabella 1 seguente, in cui ad ogni massimo e minimo di DMI/IOD, TNA,TSA (figure 3 e 4) sono stati accoppiati eventi El Nino/La Nina, separati in strong/very strong; medium; weak
Tabella 1: Coincidenze tra ENSO e DMI/IOD,TNA,TSA
| Max DMI: | 1952 | 1961 | 1971 | 1982 | 1996 | 1998 | 2008 | 2012 | 2019 | ||||||
| Min DMI: | 1959 | 1963 | 1976 | 1982 | 1991 | 1997 | 2017 | ||||||||
| Max TNA: | 1953 | 1958 | 1980 | 1988 | 1996 | 1998 | 2002 | 2005 | 2010 | 2016 | 2019 | ||||
| Min TNA: | 1949 | 1952 | 1954 | 1974 | 1976 | 1983 | 1991 | 1985 | 1987 | 1989 | 1994 | 1999 | 2010 | 2014 | 2018 |
| Max TSA: | 1973 | 1985 | 1989 | 2010 | 2016 | 2020 | |||||||||
| Min TSA: | 1951 | 1958 | 1965 | 1972 | 1977 | 1993 | 1997 | 2013 | 2018 |
El Niño/La Niña: bold=Strong, Very Strong; italic=Medium; Normal font= Weak
Questa tabella, che può essere letta anche come un istogramma orizzontale, mostra che il nord Atlantico tropicale (TNA) ha la maggiore frequenza di accoppiamento con eventi La Nina, seguita dalla frequenza di accoppiamento con eventi El Nino; il sud Atlantico tropicale mostra, per entrambi gli eventi ENSO, una frequenza minore. Nell’Oceano Indiano, DMI/IOD mostra coincidenze con ENSO ad un livello intermedio.
Le precipitazioni di Fortaleza, Brasile
DMI influenza il clima, e quindi anche il regime delle piogge, in Brasile (Sahu et al, 2010): per verificare questa affermazione riproduco la serie di piogge di Fortaleza, Brasile (3°37’09” S; 39°29’34″W).
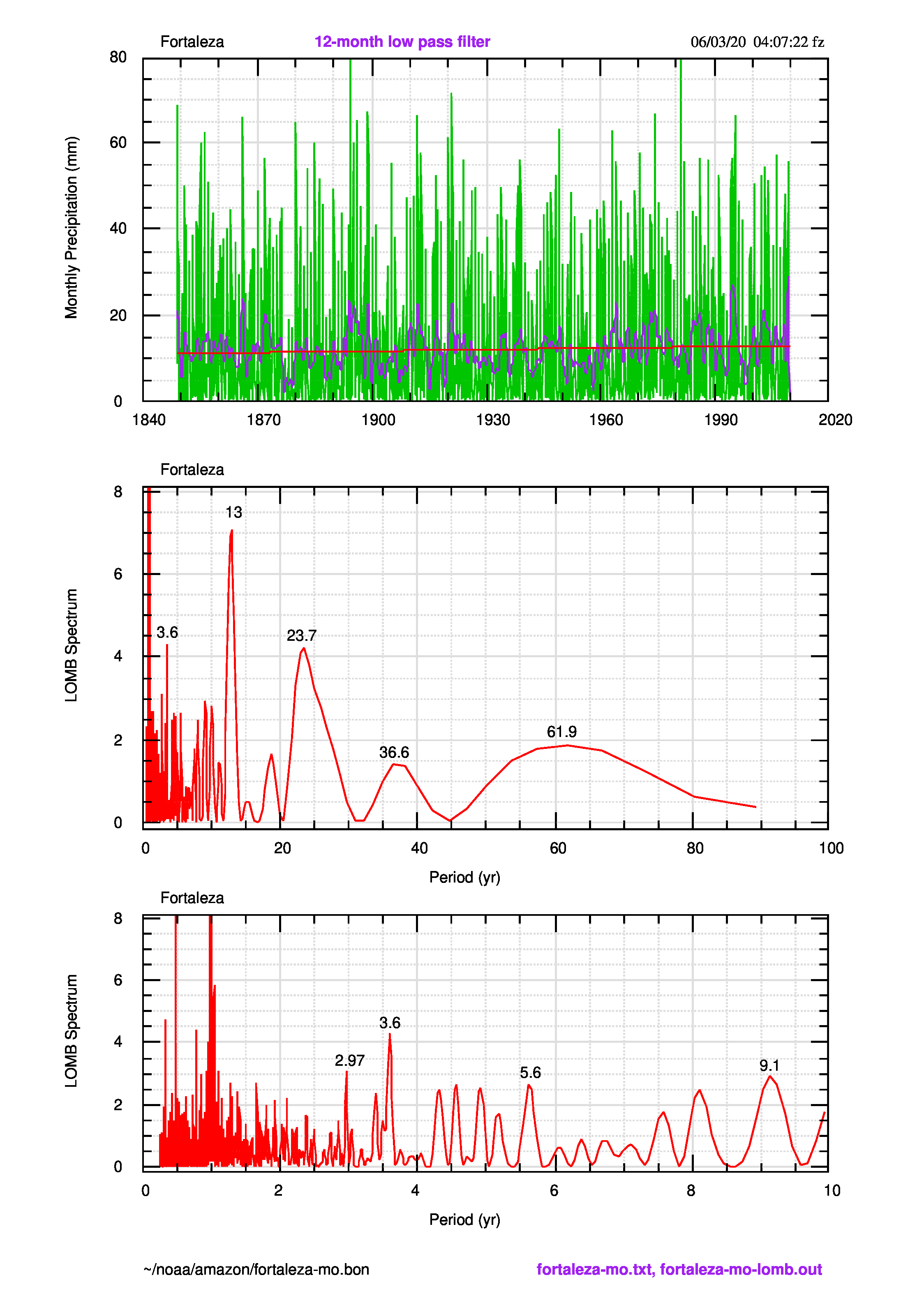
La pendenza della precipitazione ci dice che c’è stato un aumento di circa 3 mm in 160 anni e che, quindi, ci troviamo in presenza di un regime stabile nell’ultimo secolo e mezzo. I tre indici analizzati crescono tutti nel tempo e non possiamo mettere in relazione il loro aumento con la costanza delle piogge.
Il passo successivo è quello di vedere se sono i massimi spettrali degli indici ad avere influenza sulla pluviometria di Fortaleza.
A questo scopo ho fatto un confronto tra gli spettri di DMI, TNA, TSA e Fortaleza, per misurare la distanza minima tra i massimi spettrali della stazione brasiliana e di ognuno degli indici: alcuni massimi avranno lo stesso periodo, ma non si può pretenderne l’uguaglianza per tutti. Allora la distanza minore è una misura della somiglianza tra gli spettri.
Il risultato è sintetizzato nella tabella 2.
Tabella 2: Confronto tra i periodi (in anni) dei
massimi spettrali delle quattro serie
| Fortaleza | 2.97 | 3.6 | 5.6 | 9.1 | 13 | 23.7 |
|---|---|---|---|---|---|---|
| DMI/IOD | 2.98 | 5.3 | 9.6 | 11.5 | 23.8 | |
| TNA | 2.91 | 3.6 | 5.8 | 8.7 | ||
| TSA | 3.5 | 5.1 | 7.2 |
Da cui le differenze percentuali di ogni coppia Fortaleza-indice (ad esempio [(2.98-2.97)/2.98]= 0.0034= 0.3%):
- Fortaleza-DMI: 0.3%; 0%; 5.4%; 5%; 12%; 0.4% (3.6 non c’è)
- Fortaleza-TNA: 2%; 0%; 8.6%; 4.4% (13 e 23.7 non ci sono)
- Fortaleza-TSA: 2.8%; 3.8%; 21% (2.97, 13 e 23.7 non ci sono)
Conclusioni
Da questo confronto incompleto, essendo stato fatto per una sola stazione brasiliana, risulterebbe un’influenza di DMI (Oceano Indiano) sulle piogge del Brasile, come ricordato all’inizio nel paragrafo dedicato a DMI/IOD e un’influenza inferiore da parte degli indici atlatici TNA e TSA (quest’ultimo sembra avere “rapporti” più vaghi con le precipitazioni della costa atlantica).
DMI/IOD sembra avere interazioni su vasta o vastissima scala, anche ricordando quanto derivato dalla tabella 1 sulle interazioni con ENSO.
Quest’ultima affermazione contraddice quanto ricordato all’inizio sulla indipendenza tra DMI/IOD ed ENSO, ma i numeri riportati in tabella 1 fanno pensare che una qualche forma di interazione abbia luogo tra i due modi oceanici.
Bibliografia
- David B. Enfield, Alberto M. Mestas-Nufiez, Dennis Luis Cid-Serrano: How ubiquitous is the dipole relationship in tropical Atlantic sea surface temperatures?, JGR, 104, C4, 7841-7848, 1999. https://doi.org/10.1029/1998JC900109
- Hu S., Fedorov A.V.: Indian Ocean warming can strengthen the Atlantic meridional overturning circulation, Nature Climate Change, 9, 747-751, 2019. https://doi.org/10.1038/s41558-019-0566-x
- Mary T. Kayano, Rita V. Andreoli and Rodrigo A. Ferreira de Souza: Relations between ENSO and the South Atlantic SST modes and their effects on the South American rainfall , International Journal of Climatology , 33, 2008-2023, 2013. https://doi.org/ 10.1002/joc.3569
- Netrananda Sahu, Yosuke Yamashiki and Kaoru Takara: Impact Assessment of IOD/ENSO in the Asian Region , Annuals of Disas. Prev. Res. Inst, Kyoto Univ., No.53 B, 2010. Full text locale (l’articolo è disponibile in una pubblicazione dell’Università di Kyoto)
- N. H. Saji, B.N. Goswami, P.N. Vinayachandran & T. Yamagata: A dipole mode in the tropical Indian Ocean, Nature, 401, 360-363, 1999, full text
| Tutti i dati e i grafici sono disponibili nel sito di supporto |


Caro Franco, in questi giorni sono molto impegnato: la chiusura delle scuole e la necessità di organizzare delle lezioni “a distanza”, mi porta via molto più tempo delle normali lezioni, per cui mi sono quasi estraniato dalla vita di CM. Oggi, domenica, sono ritornato a leggere CM ed ho avuto la gradita sorpresa del tuo articolo. Ribadisco l’osservazione che ho fatto in occasione del precedente post su ENSO: questi eventi che determinano gli indici di cui ti occupi nell’articolo, sono del tutto imprevedibili.
Una cosa mi ha incuriosito, però: il trend di tutti e tre gli indici che hai preso in esame. Dal 1950 sono tutti in aumento. Hai per caso trovato negli articoli che hai spulciato una spiegazione fisica per questo andamento?
Ciao, Donato.
Caro Donato,
capisco che il dover cambiare a scuola una struttura mentale consolidata con un’altra che ufficialmente funziona ma che immagino presenti ancora diversi
problemi, possa creare situazioni complicate (di varia natura), per cui hai tutta la mia comprensione il mio appoggio morale, e, posso immaginare, non solo il mio.
Per la questione del riscaldamento, dato che questi indici hanno le dimensioni di una temperatura (SST), penso che seguano l’andamento dell’Oceano globale.
Tu parli del 1950 come anno di inizio dell’aumento
della temperatura e la stessa cosa fanno Hu e Federov (2019) per l’Oceano Indiano tropicale (TIO), attribuendo il ricaldamento di 0.1 C/decennio al “global warming”. Non ho altre informazioni e penso di poter concordare con questi autori (a meno delle cause del global warming). I fit lineari calcolati dall’inizio della serie, che trovi nelle figure dei tre indici (un “+-” mi è rimasto nella tastiera, per il valore della pendenza) hanno trend molto inferiori ma si vede bene che nel 1950 c’è stato un cambiamento. Anche
se l’articolo è liberamente disponibile, accludo la figura 2 di Hu e Fedorov che mostra il riscaldamento dal 1950.
Ciao. Franco
Immagine allegata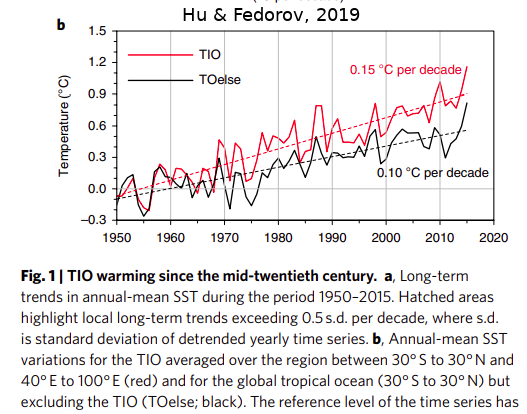
Gentile Zavatti,
Nel ringraziarla per il contributo vorrei chiederle un chiarimento sul passaggio “El Nino/La Nina (ENSO) che è il più importante modo di oscillazione (non periodico) dell’Oceano Pacifico”.
Un’oscillazione non periodica sembra un non senso. Il concetto di oscillazione rinvia in effetti a un fenomeno che ritorna con una certa periodicità, anche se identificare questa periodicità non è sempre ovvio date le numerose interferenze esterne.
Nell’Atlantico settentrionale l’indice AMO (Atlantic Multidecadal Oscillation) è a volte sostituito dall’AMV (Atlantic Multidecadal Variation), che integra la componente oscillatoria interna all’oceano (AMO) e altri fattori esterni come l’attività solare, le eruzioni vulcaniche e gli effetti antropici (ex. Wang et al., 2017, Nature Geoscience, https://www.researchgate.net/publication/318136123_Internal_and_external_forcing_of_multidecadal_Atlantic_climate_variability_over_the_past_1200_years).
Forse anche per El Niño/La Niña si dovrebbe operare la stessa distinzione, magari separando le manifestazioni ordinarie da quelle ‘strong’. Queste ultime sembrano rispettare una certa periodicità che, come avevo scritto in un mio commento a un suo precedente post (http://www.climatemonitor.it/?p=46742), sarebbe la medesima ciclicità di circa 18 anni della luna (ex. El Niño-strong 1982-1983, 1997-1998, 2015-2016).
La ringrazip per ogni chiarimento che vorrà darmi.
Il concetto di oscillazione non implica necessariamente quello di periodicità ed ENSO è un tipico esempio del fatto che pur conoscendo le sue
principali periodicità (diciamo tra 2 e 7 anni più una a 10-12 anni) i modelli di circolazione generale (GCM) non trattano questa interazione oceano-atmosfera e, soprattutto, non sono in grado di prevedere i suoi
innesco e durata. Credo ci sia qualche tentativo di modellare ENSO ma solo a livello sperimentale, v. ad esempio
https://www.nature.com/articles/s41598-018-33340-y.
C’è anche questa ben nota pubblicazione NOAA
https://www.cpc.ncep.noaa.gov/products/analysis_monitoring/lanina/enso_evolution-status-fcsts-web.pdf
che ogni anno, a febbraio-marzo, produce lo stato oceano-atmosfera del Pacifico equatoriale e, alla fine, il grafico di previsione dell’ENSO successivo: basta guardarlo per vedere la grande incertezza della previsione.
Quindi il “non periodico” si riferisce al fatto che non siamo in grado di prevedere l’accendersi di El Nino/La Nina e, in definitiva, di prevedere il modo di combinarsi dei suoi periodi principali con l’ambiente circostante
(ad esempio variazioni delle correnti, della salinità o dei venti).
Per la periodicità di 18 anni degli El Nino strong, nel mio post del 26 febbraio scorso http://www.climatemonitor.it/?p=52453 ho pubblicato lo spettro dell’indice ONI (Oceanic Nino Index) da cui non appare in alcun modo un periodo di circa 18 anni. Se davvero la periodicità degli “strong” fosse stata quella che lei indica, lo spettro avrebbe dovuto darne conto, per cui non saprei cosa rispondere. Se fosse possibile ipotizzare una
dipendenza/influenza di tipo astronomico, di certo non mi tirerei indietro e non cercherei di minimizzarla. Franco
Grazie per la gentile risposta.
Il ciclo nodale della luna di circa di 18 anni e mezzo puo’ essere un candidato per spiegare le variazioni quasi bi-decadali osservate in certe regioni del globo. Il lavoro di Agosta del 2013 (https://rmets.onlinelibrary.wiley.com/doi/full/10.1002/joc.3787) suggerisce questa oscillazione per spiegare le variazioni delle temperature oceaniche che determinano l’indice SWSA (da lei evocato nel suo post), a loro volta riflesse nella variabilità delle piogge estive nella catena delle Ande.
Comprendo che il cammino è ancora lungo per trovare una connessione con l’ENSO.
Grazie per l’articolo di Agosta,2014; davvero interessante, tanto che sono tentato di scrivere all’autore per avere i dati SRI che lui usa per calcolare lo spettro MMT. Sono incuriosito dalla sua figura 2 b) e c) dove l’aggiunta di 35 anni nel calcolo dello spettro produce ben visibili differenze (scompare il picco a 25 anni e quello a 18.6 anni, ad esempio). Nel 2016 ho scritto un post (http://www.climatemonitor.it/?p=39988) dove calcolo lo spettro delle piogge di Fortaleza dimezzando due volte il numero dei dati e trovando una ragionevole continuità e costanza nei massimi spettrali, a differenza di Agosta per il quale scompaiono letteralmente (o almeno sembra così dalla figura) i picchi più potenti.
Mi ha trattenuto finora (ma continuo a pensarci e probabilmente lo farò) dal chiedere i dati il fatto che sono vecchi di più di 7 anni (articolo spedito a gennaio 2013) e forse sono finiti in qualche “dimenticatoio” dell’autore. E, sì, credo anche io che la strada verso una completa comprensione di ENSO sia ancora lunga. Franco
Chiedere è sempre lecito. Gli autori useranno la cortesia di risponderle.
Mi pemetto di segnalarle anche l’abstract EGU del 2016 di Serykh e Sonechkin: https://ui.adsabs.harvard.edu/abs/2016EGUGA..18….8S/abstract.
Da notare, come driver ENSO, tre periodicità concatenate: gli 11 anni del ciclo solare, i 14 mesi dell’oscillazione (detta di Chandler) dell’asse di rotazione terrestre rispetto alla Terra stessa e i 18 anni e mezzo del ciclo lunare.
Buon lavoro.
quale ruolo svolze la ITCZ ( zona di convergenza intertropicale ) nella definizione degli indici citati?
Hu e Fedorov (2019) già nel titolo dicono che il riscaldamento dell’Oceano Indiano (e quind DMI/IOD) può rafforzare AMOC e nell’abstract si dice che ITCZ si sposta verso nord.
Kayano et al.,(2013) fanno riferimento al solo TSA (o ai South Atlantic SST modes) e dicono: “So, the main seasonal system modulating the rainy season in this area, the Atlantic intertropical convergence zone (ITCZ) (Ratisbona, 1976; Hastenrath and Heller,1977), is affected by the ENSO.”
Penso che gli effetti degli indici siano in buona parte sovrastati dagli effetti di ENSO.
Tu chiedi il ruolo di ITCZ “nella definizione” degli indici: direi che ITCZ non ha alcun ruolo. Nella pratica produce variazioni della SST (ma non so di
quale entità) e probabilmente ha un ruolo “nella misura” degli indici. Franco