L’esponente di Hurst e gli spettri – Parte III – Nuove applicazioni

Livello del Nilo
L’altezza del Nilo -livello minimo dal 622 al 1469 CE- ha un esponente di Hurst H=0.833 e quindi si presta alla procedura descritta nel primo articolo di questa serie. I dati, annuali, sono a passo costante per cui uso le differenze.

In figura 13 (pdf) mostro le funzioni di autocorrelazione delle due serie (osservata e delle differenze).

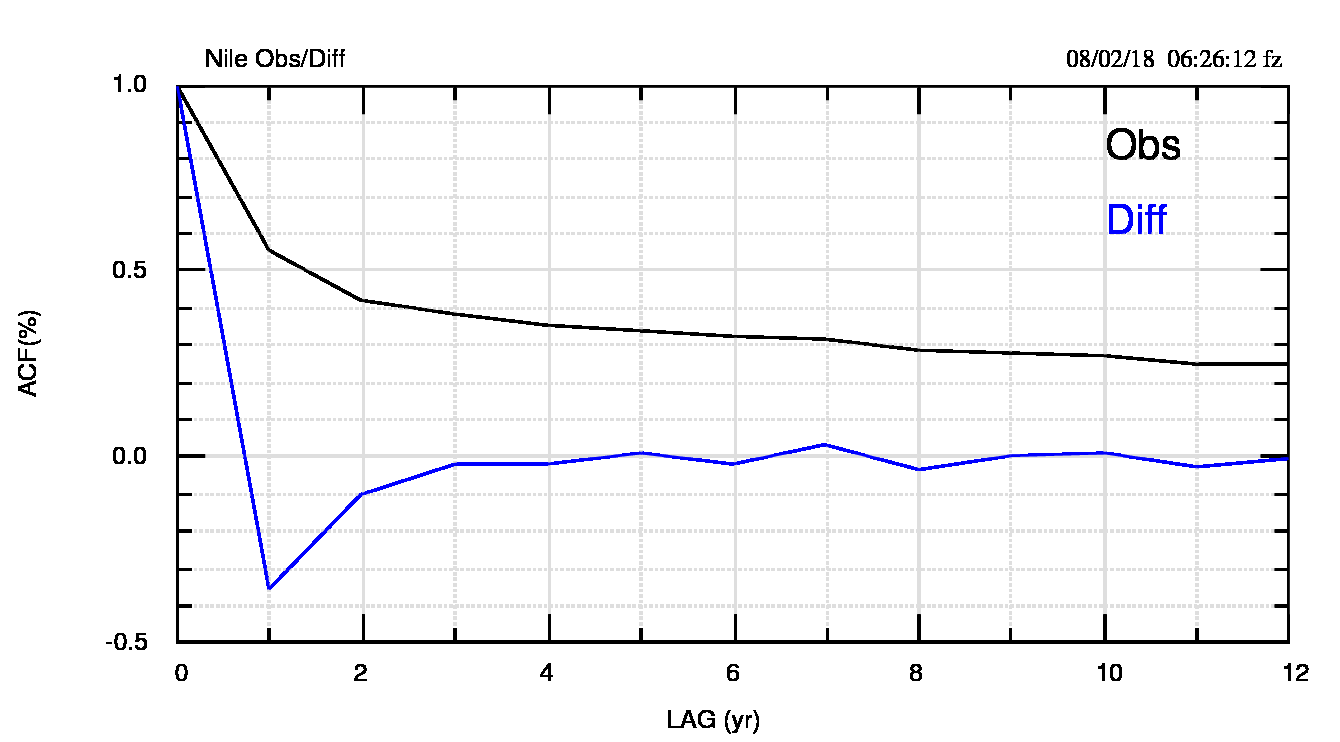
La acf(1) dei dati osservati è di poco superiore a 0.5 e quindi, per quanto si era detto all’inizio del primo articolo di questa serie, la persistenza non dovrebbe avere un ruolo preponderante. Malgrado questo, però l’acf delle differenze mostra un evidente miglioramento.

Gli spettri della serie osservata e delle differenze d(i)=t(i+1)-t(i) sono in figura 14 (pdf) e in figura 15 (pdf).

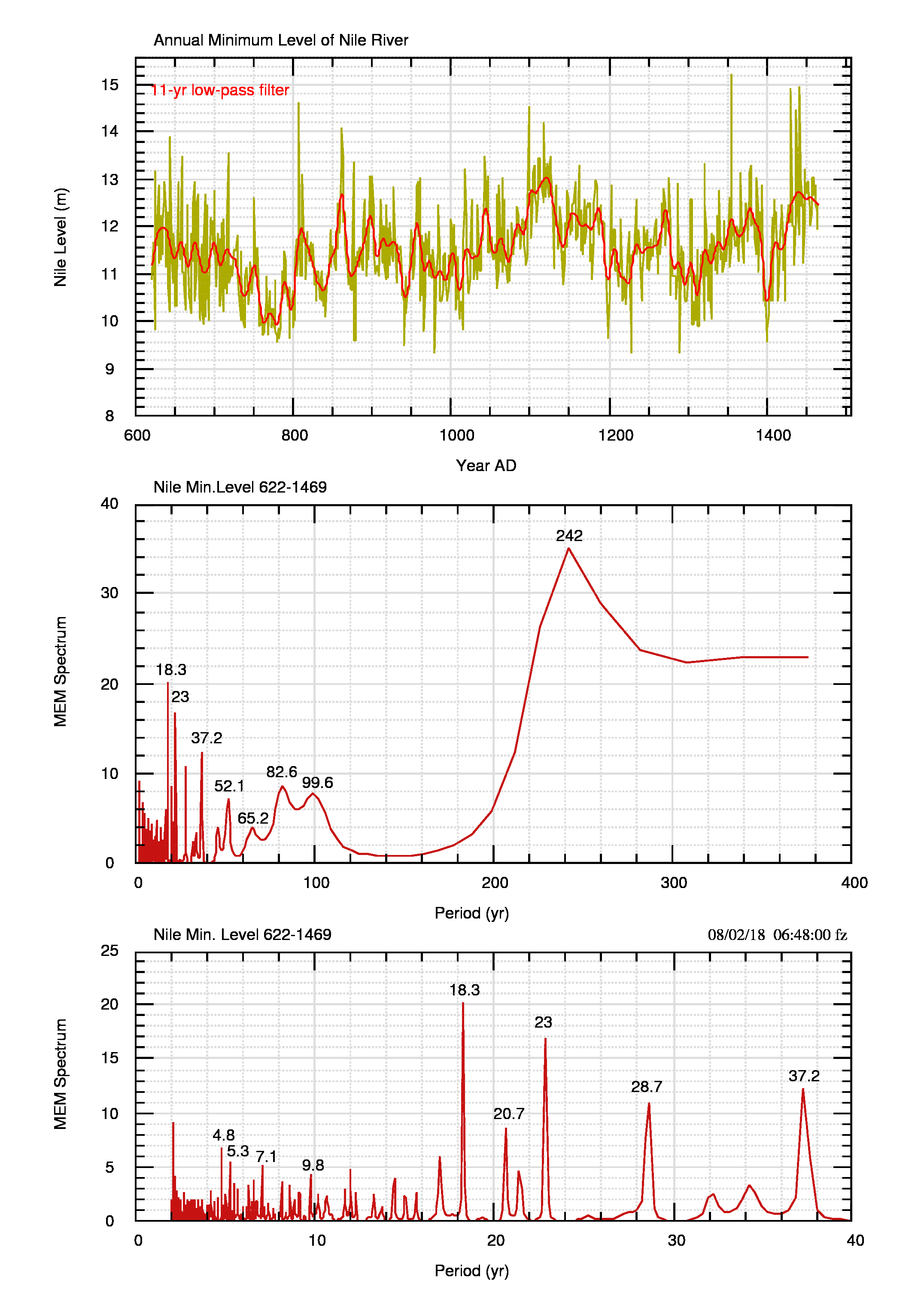
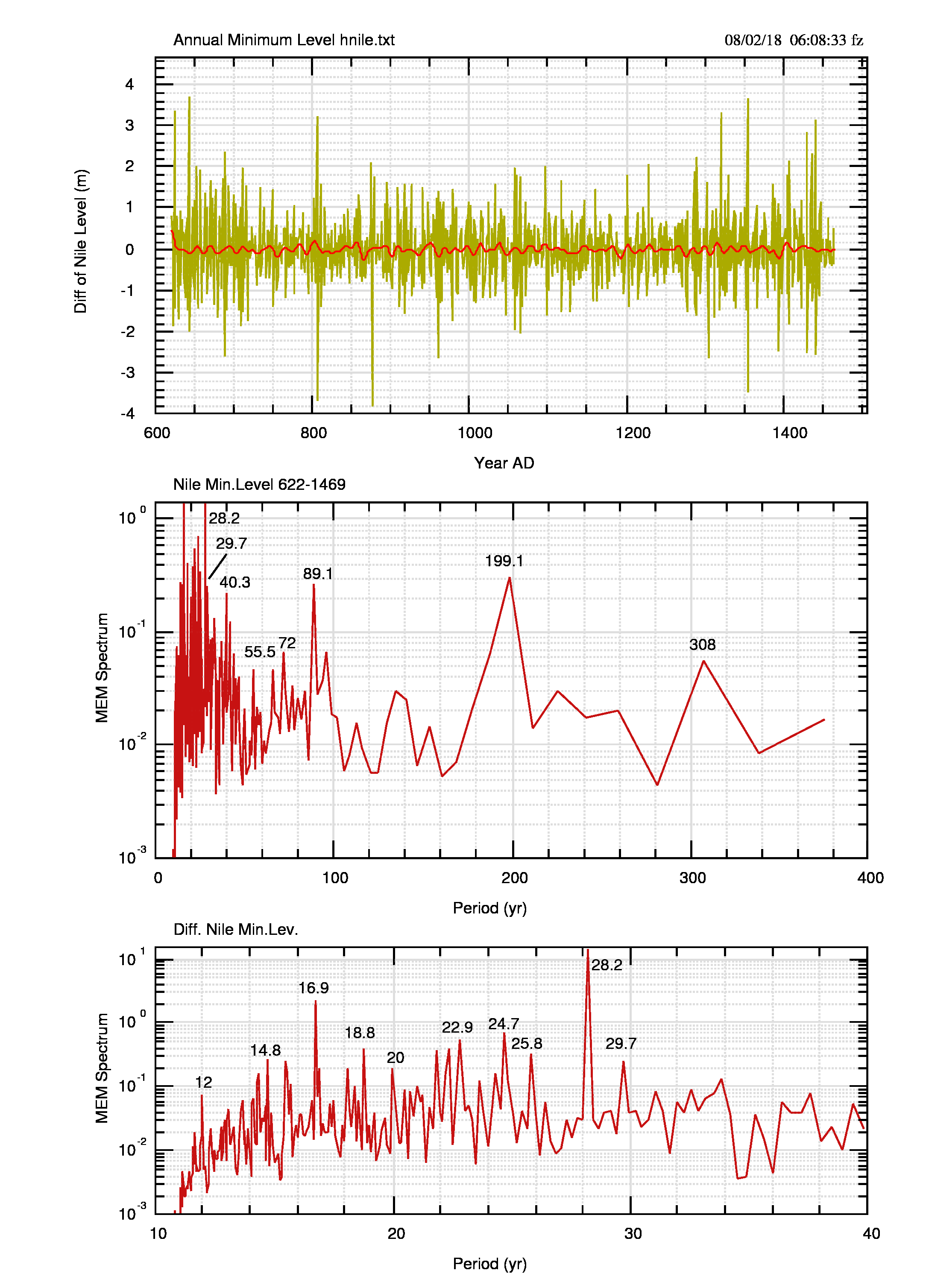
Il confronto tra gli spettri mostra che:

1. Una increspatura nello spettro “osservato” a 320-340 anni, praticamente invisibile se non in maniera meno vaga nei dati numerici, viene evidenziata dalle differenze come un massimo a 308 anni.
2. Il massimo a 242 anni “osservato” viene scomposto nelle differenze come un massimo a 199 anni e due massimi minori a circa 225 e 260 anni.
3. I massimi “osservati” a 82.6 e 99.6 anni diventano 89.1 e 96.7 anni (il massimo minore non è indicato in figura 15). Il massimo principale delle differenze, a 89.1 anni, risulta netto e meglio definito rispetto ai massimi dei dati osservati.
4. I massimi di periodo inferiore sono quasi ugualmente presenti nei due spettri. Si nota la mancanza del periodo di 37.2 anni, apparentemente sostituito nelle differenze da quello a 40.3 anni.
5. Qui, rispetto ai casi precedenti, in modo più evidente cambiano i rapporti tra le potenze dei massimi negli osservati e nelle differenze.

In casi come questo, dove lo spettro cambia abbastanza nei due casi, l’uso delle differenze permette una migliore definizione dei massimi spettrali, eliminando quei picchi per i quali una giustificazione fisica si può fornire con (molta) difficoltà.

TPW (Total Precipitable Water)
Dell’acqua precipitabile totale si è parlato su CM (vedere i anche i link ad articoli precedenti e i commenti). Questa variabile è strettamente legata alla temperatura e raggiunge i suoi valori massimi lungo la fascia equatoriale del Pacifico, soprattutto in quei mari dell’Indonesia chiamati “warm pool” dove si accumula l’acqua calda trasportata dagli alisei durante El Niño. La somiglianza tra temperatura globale e TPW è evidenziata in figura 16 (pdf), dove TPW è scalata ai valori di HadCrut4.

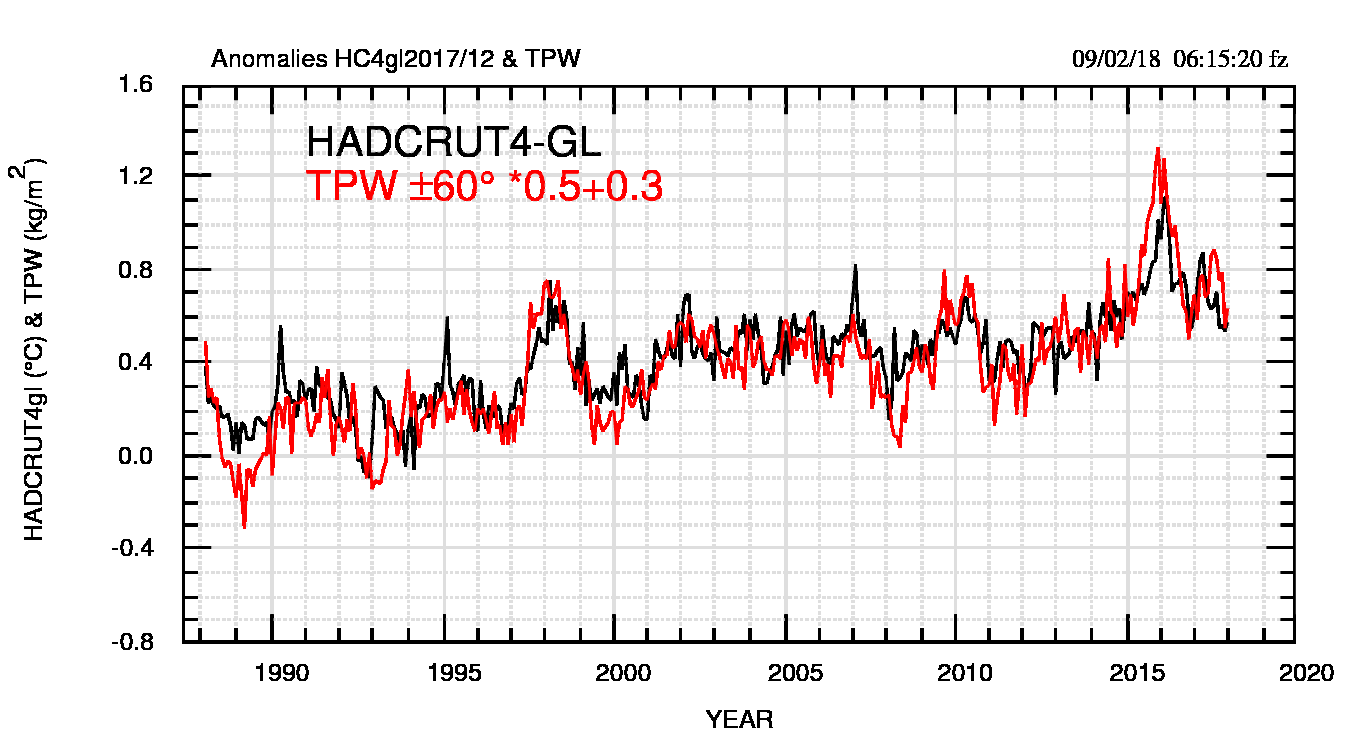
La misura di TPW è disponibile per le due fasce di latitudine ±20° e ±60°; qui viene usata solo la fascia più ampia.
Anche solo la somiglianza con la temperatura porta a pensare alla presenza del fenomeno della persistenza e all’uso delle differenze per eliminarla o almeno diminuirla. Infatti il confronto tra le funzioni di autocorrelazione dei dati osservati e delle differenze di figura 17 (pdf) mostra che le differenze hanno completamente annullato la persistenza.

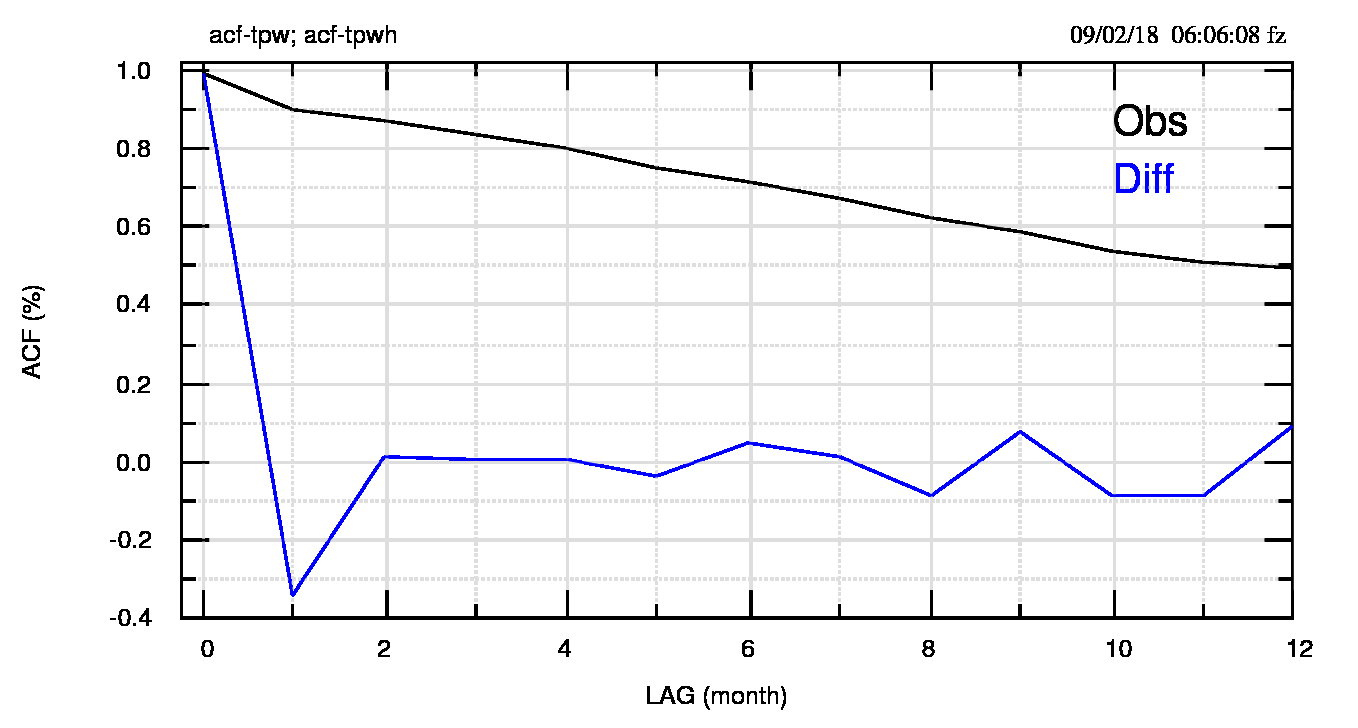
Anche l’analisi spettrale dei dati osservati e delle differenze riportata in figura 18 (pdf) e in figura 19 (pdf) conferma l’ormai noto cambiamento tra la potenza dei picchi e, ancora una volta, la non influenza della persistenza sul periodo dei massimi spettrali

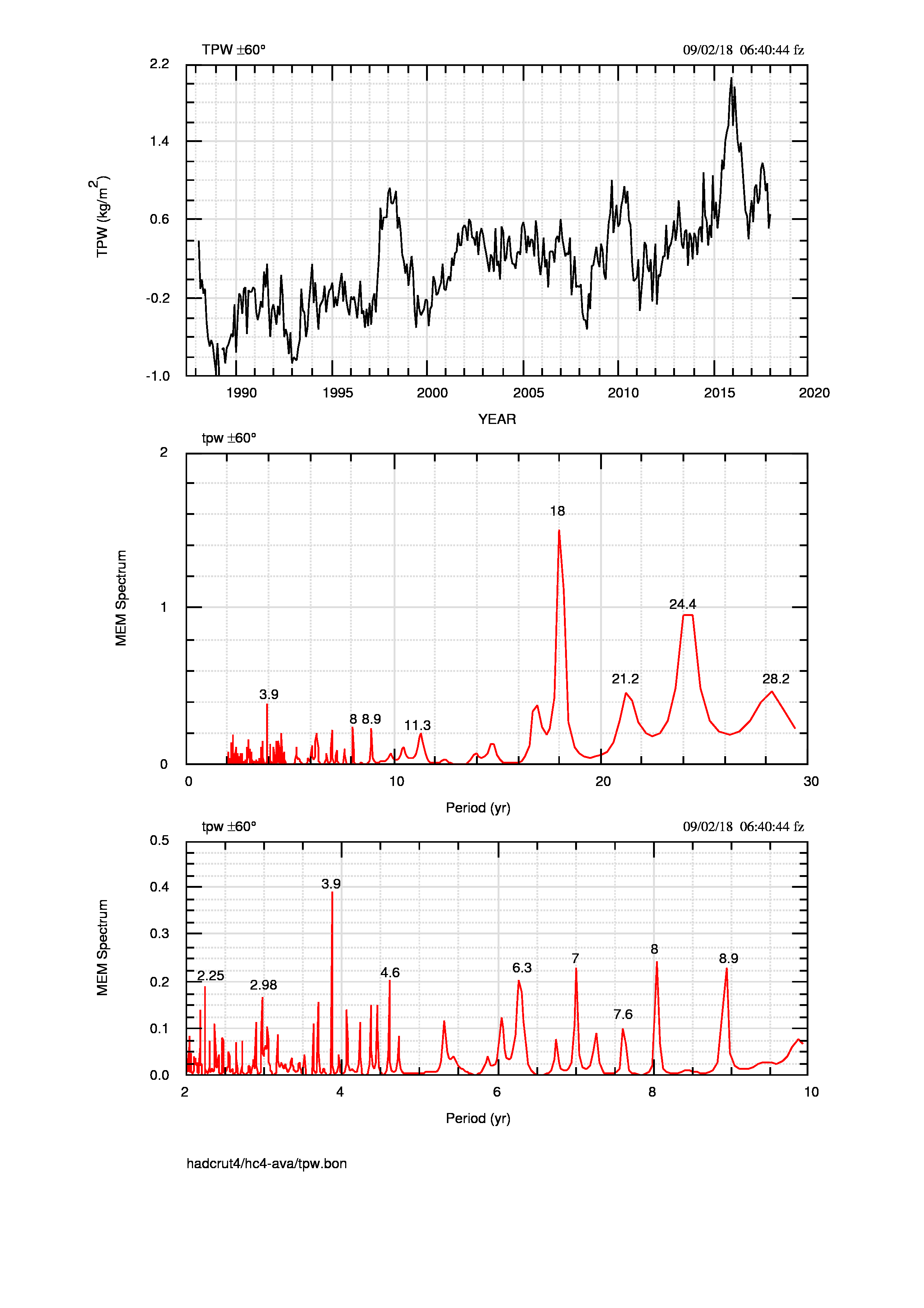
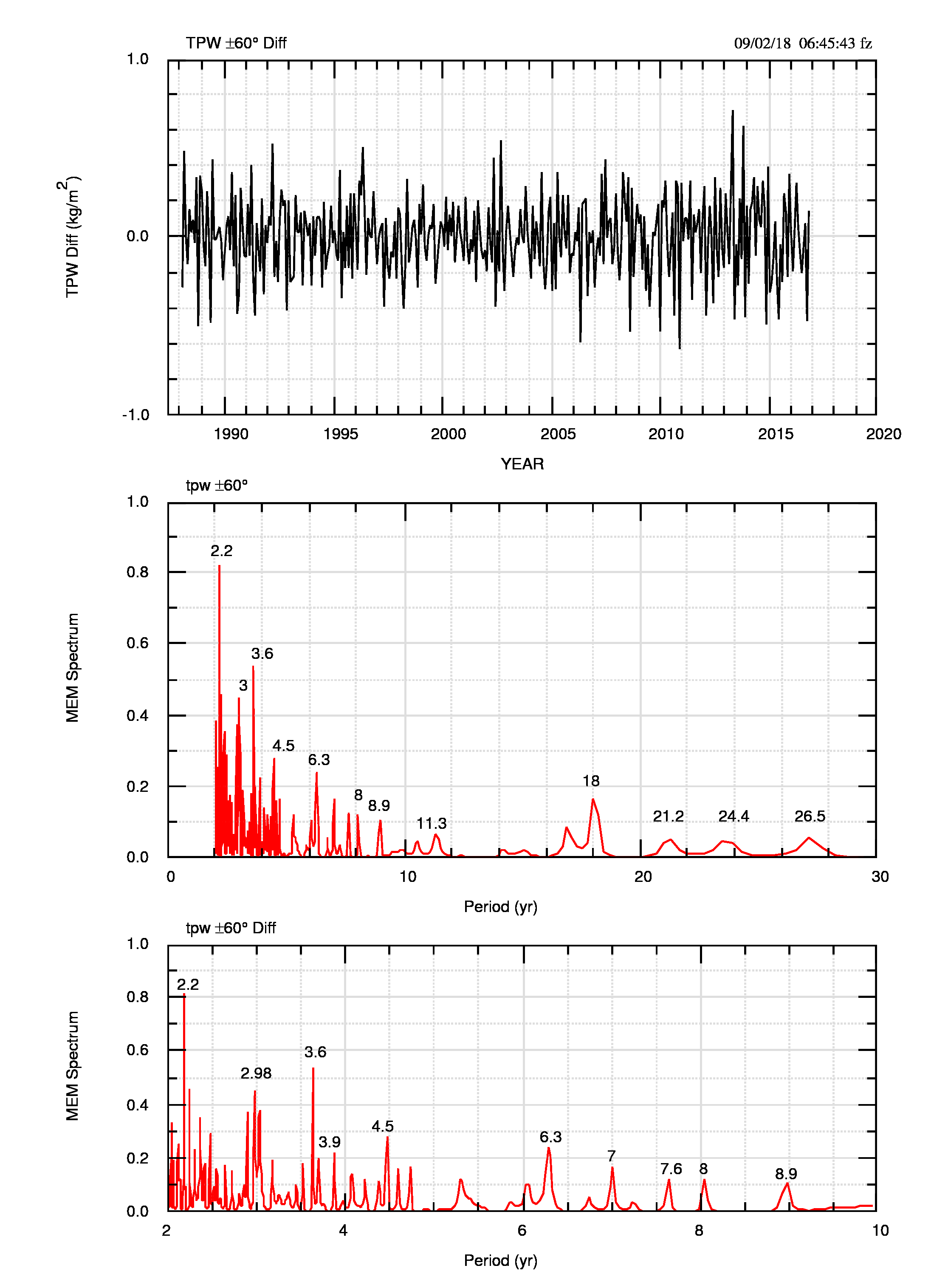
In questo caso qualche dubbio può sorgere a causa della brevità della serie (30 anni) ma credo che il confronto con le anomalie NOAA (annuali e mensili) delle figure 5 e 12 possa risolvere positivamente questi dubbi, in quanto la stessa cosa succede per serie ben più lunghe.

Con questo termino la serie di articoli dedicati alla persistenza, nella speranza di aver chiarito quale può essere il peso di questo fenomeno sugli spettri delle serie climatiche.