L’esponente di Hurst e gli spettri (Parte I)

Riassunto: Sostituisco il dataset iniziale con le sue differenze prime (o con le derivate numeriche in caso di passo variabile) e verifico sperimentalmente se l’esponente di Hurst H, cioè il livello di persistenza, cambia nel senso che si avvicina maggiormente al valore 0.5 mentre il dataset trasformato mantiene l’informazione spettrale del dataset originale. Applico la modifica alle medie annuali NOAA di anomalia di temperatura, ad all’ultimo dataset mensile, sempre NOAA, e al livello del lago Vittoria i cui dati non sono a passo costante.
Abstract: I change the original dataset with its differences or its numerical derivatives in case of a variable step and look at the Hurst exponent H. If its value is lowered by this procedure, I verify if the new dataset contains again the spectral information of the original one by comparing their spectra. Such a procedure has been applied to the yearly global temperature anomaly and to the last available monthly data from the NOAA GHCN cag-site. Also the lake Victoria levels (at variable time step) has been used to test the procedure.

Si è verificato, ormai diverse volte, che il problema della persistenza riguarda molti dataset che si usano abitualmente in climatologia, e non solo. La persistenza, che consiste in risultati che tendono a riprodurre i risultati precedenti, mostra che i dati sono autocorrelati e che potrebbero non essere indipendenti. La funzione di autocorrelazione a lag 1 [ACF(1)] in questo caso può assumere valori maggiori di 0.5, denotando in pratica che la statistica “normale” non può più essere usata in quanto basata su dati indipendenti.
Ricordo sempre, a me stesso, che due variabili aleatorie (v.a., cioè in pratica i dati) indipendenti sono scorrelate, mentre non è vero il viceversa: dati (v.a.) scorrelati non sono necessariamente indipendenti. Se i dati sono correlati, la loro indipendenza deve essere dimostrata per altra via.
Ad esempio, la deviazione standard della media di un campione

std dev(Xn)=σ/sqrt(n)=σ/n^0.5       (1)
con Xn media di un campione di n elementi e σ deviazione standard (comune) degli elementi del campione, nel caso di fenomeni che contengono la persistenza, diventa (Koutsoyiannis, 2003):
std dev(Xn)=σ/n^(1-H)      (2)

con H esponente (o coefficiente) di Hurst. Se H=0.5 le due espressioni precedenti diventano uguali e questo ci permette di dire che la serie da cui abbiamo ricavato il valore di H non ha persistenza e quindi, sbagliando, possiamo dire che le variabili aleatorie, i cui valori compongono la serie in esame, sono indipendenti (l’indipendenza potrebbe essere dimostrata verificando che la densità di probabilità congiunta delle due v.a. f(x,y) è data dal prodotto delle densità di probabilità delle singole v.a. g(x)•h(y), cioè f(x,y)=g(x)•h(y)).

L’esponente di Hurst, H, viene normalmente stimato attraverso un processo semplificato ma ancora non semplice da seguire (Koutsoyiannis, 2002, 2003): per questo motivo io uso una procedura probabilmente non corretta che però fornisce facilmente un valore approssimato di H.

Come stima di H io uso l’equazione (5) di Koutsoyiannis (2003) (che poi è l’equazione (17) di Koutsoyiannis, 2002):

ρ_j^(k)=ρ_j=H•(2H-1)• j^2H-2       (3)
(si dimostra che questa equazione è indipendente da k),
in cui ρ_j è la funzione di autocorrelazione a lag j (o acf(j), j>0.
Usare l’eq.(3) con lag 1 porta a
acf(1)=2H²-H  o   2H²-H-acf(1)=0,
da cui
H=(1+sqrt(1+8•acf(1)))/4.       (4)

Quindi stimo H a partire da acf(1), il che ovviamente implica il calcolo della funzione di autocorrelazione. Da notare che acf è una funzione positiva, compresa tra 0 e 1, e che, se il calcolo fornisce una acf negativa, l’eq.(4) assume un valore indefinito (NaN, not a number). I valori negativi possono essere considerati fluttuazioni attorno allo zero e si può assegnare loro il valore zero, ottenendo così H=0.5 (cioè dati scorrelati).

Vediamo ora tre applicazioni.

Medie annuali delle temperature globali NOAA
Ogni fine anno, dal 2011, raccolgo le anomalie globali NOAA-NGHC (terra+oceano), delle quali in figura 1 (pdf) mostro un esempio relativo al 2017.

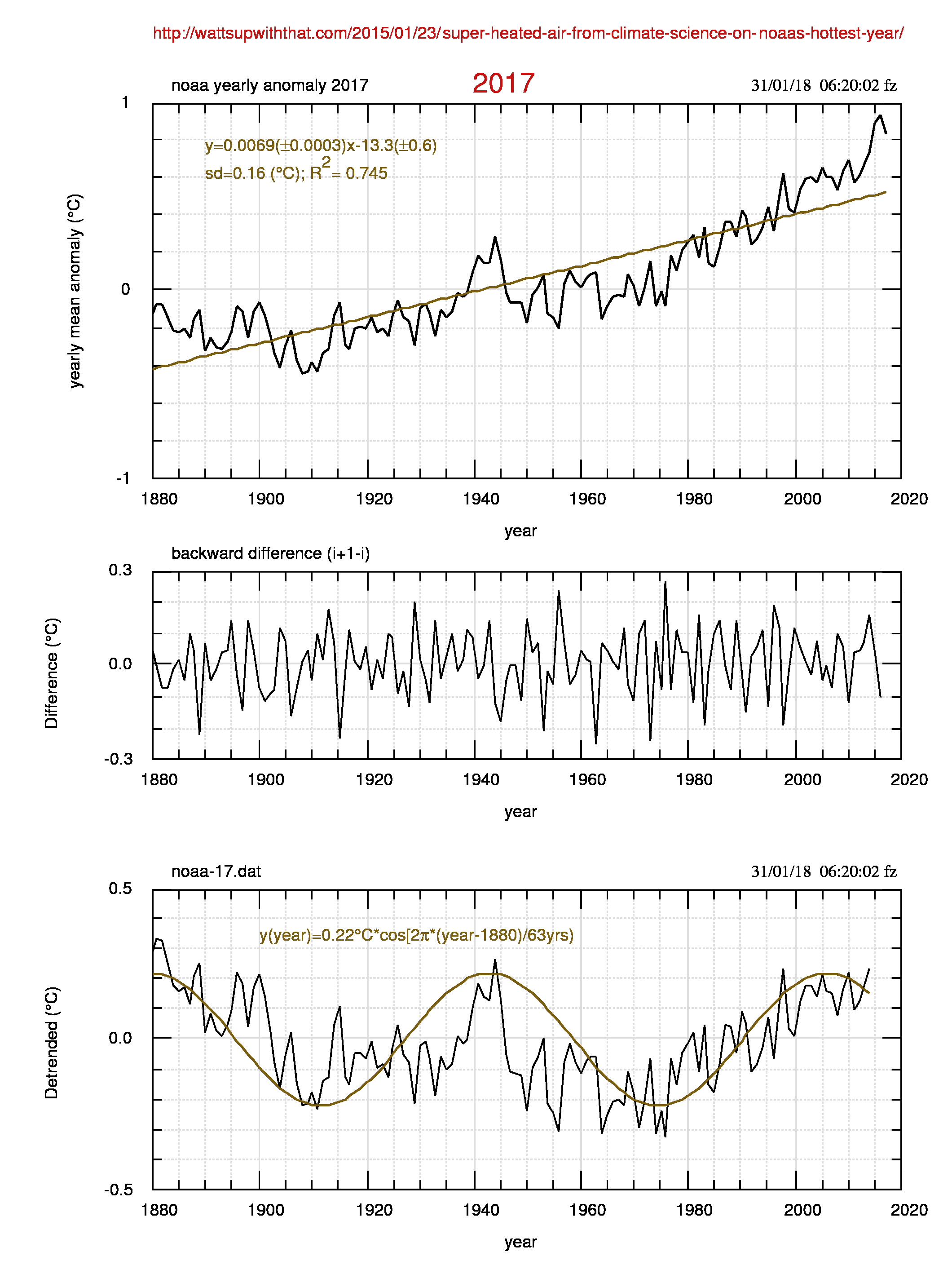
Insieme ai dati osservati mostro la serie delle differenze d(i)= t(i+1)-t(i) e il confronto dei residui (i detrended) con una sinusoide fissa. Come si vede nella successiva fig.2 (pdf), la acf(1) -e quella ad altri lag- sono molto elevate e indicano valori di H stimati dall’eq.(4) vicini ad 1 e quindi dati soggetti ad una forte persistenza. Infatti H va dal valore 0.974 per il 2011-2014 ai valori 0.970 (2015), 0.972 (2016), 0.975 (2017).

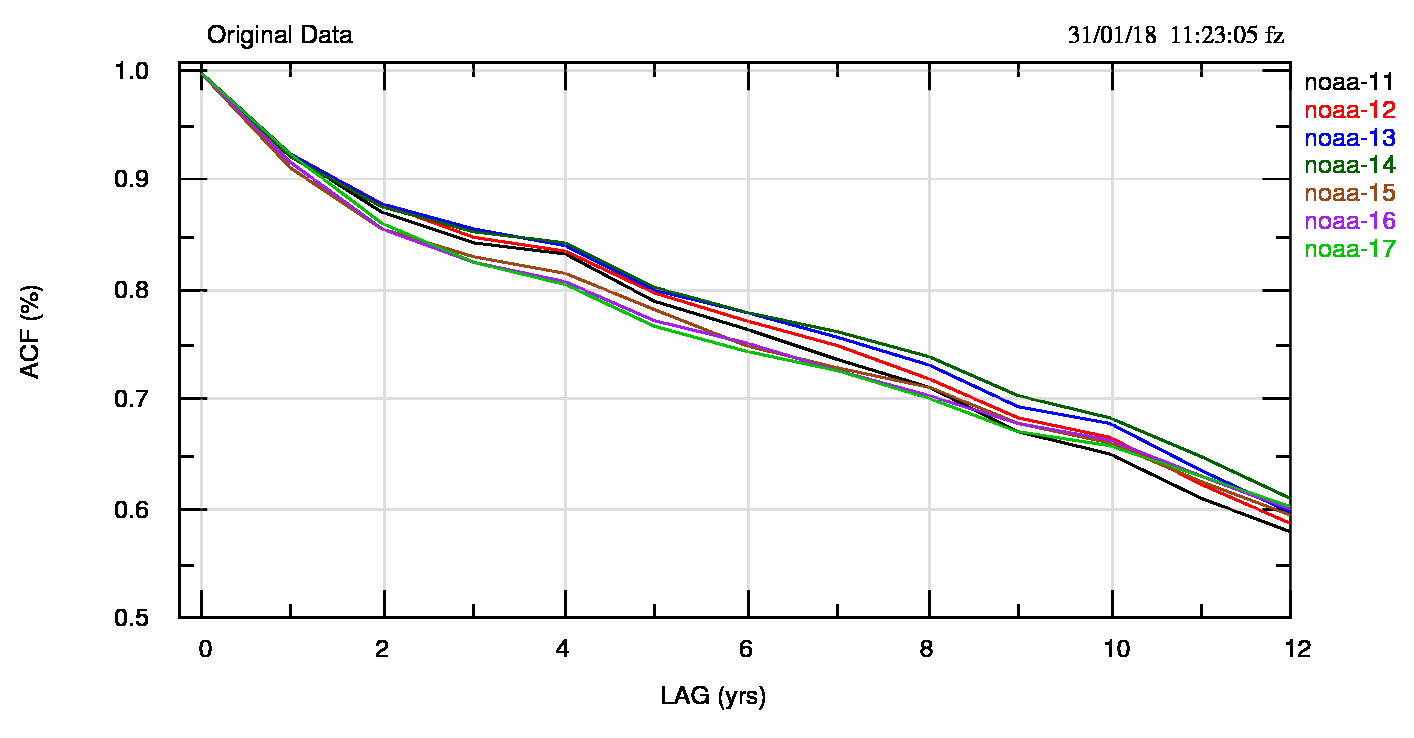
La persistenza dovrebbe anche generare periodi spuri nell’analisi spettrale.

Rileggendo un articolo del 2015 su WUWT di Roman Mureika sulla persistenza, ho visto che lui, in altro contesto, usa le differenze tra i valori per mostrare che sono scorrelate (Murieka in realtà usa un contorto giro di parole: “potrebbe non essere irragionevole assumere che i cambiamenti annuali siano indipendenti l’uno dall’altro”. Le contorsioni derivano direttamente dalle righe in rosso scritte più in alto). Ho ripreso il suo esempio per i dati annuali NOAA e ho verificato, v. fig.3 (pdf), che le acf delle differenze sono nulle a lag 1.

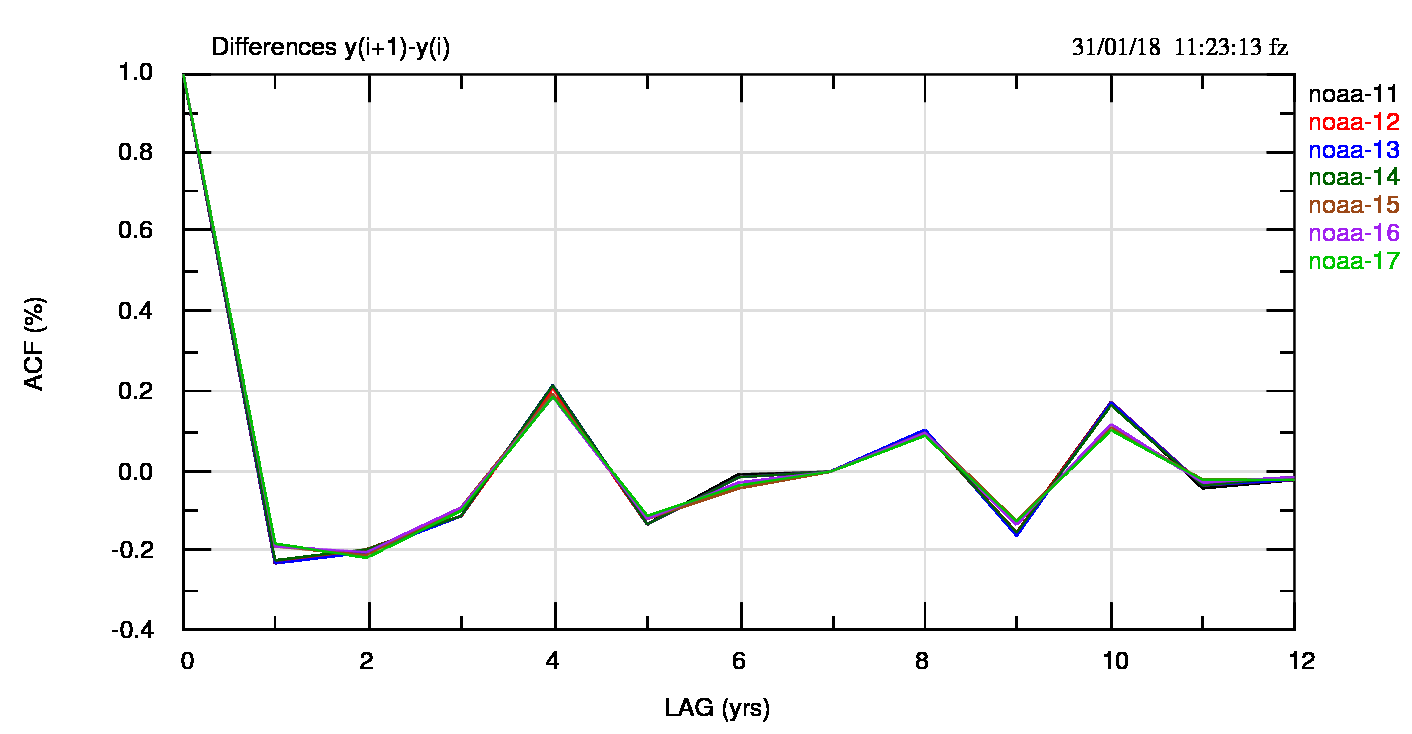
Quindi la trasformazione da anomalia a differenza di anomalia ha prodotto una serie in cui non è presente la persistenza e che dovrebbe mantenere le informazioni presenti nella serie originale (o almeno parte di esse).

Per i miei scopi, mi chiedo in particolare se la serie derivata (le differenze) ha ancora in sé l’informazione spettrale della serie originale (l’anomalia di temperatura). Se così fosse, potrei applicare l’analisi spettrale alle differenze, senza il rischio di generare periodi spuri che dipendano dalla persistenza.
Dubito di riuscire a dimostrare in modo generale questa proprietà di mantenimento dell’informazione, anzi sono quasi certo del contrario, per cui proverò a verificarla empiricamente calcolando lo spettro (MEM; i dati sono a passo costante e senza “buchi”) della serie originale e di quella derivata e confrontando i due output.
Ho fatto questa operazione per le 7 serie di cui dispongo e mostro qui il caso del 2017, in fig.4 (pdf) e in fig.5 (pdf).

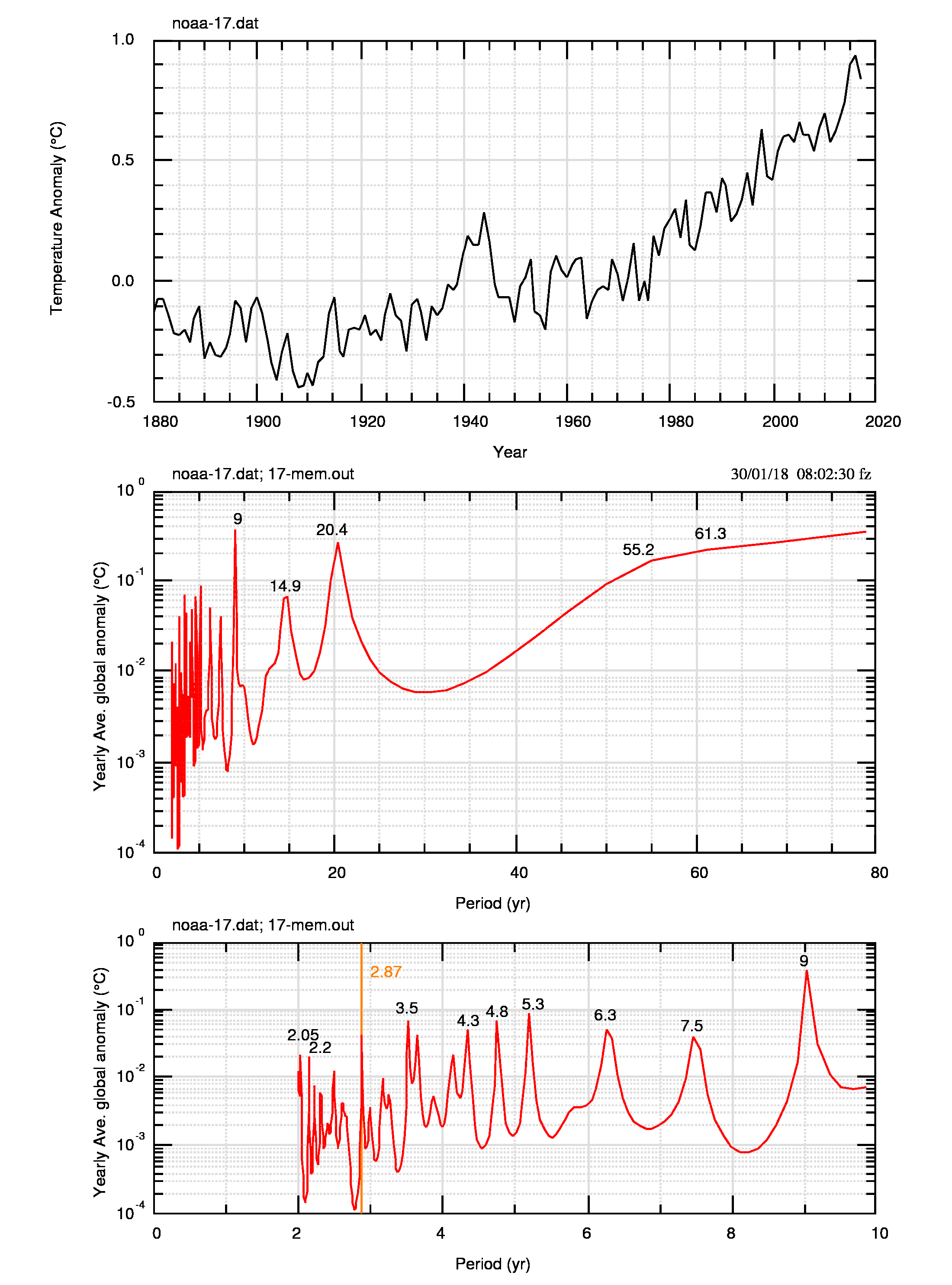
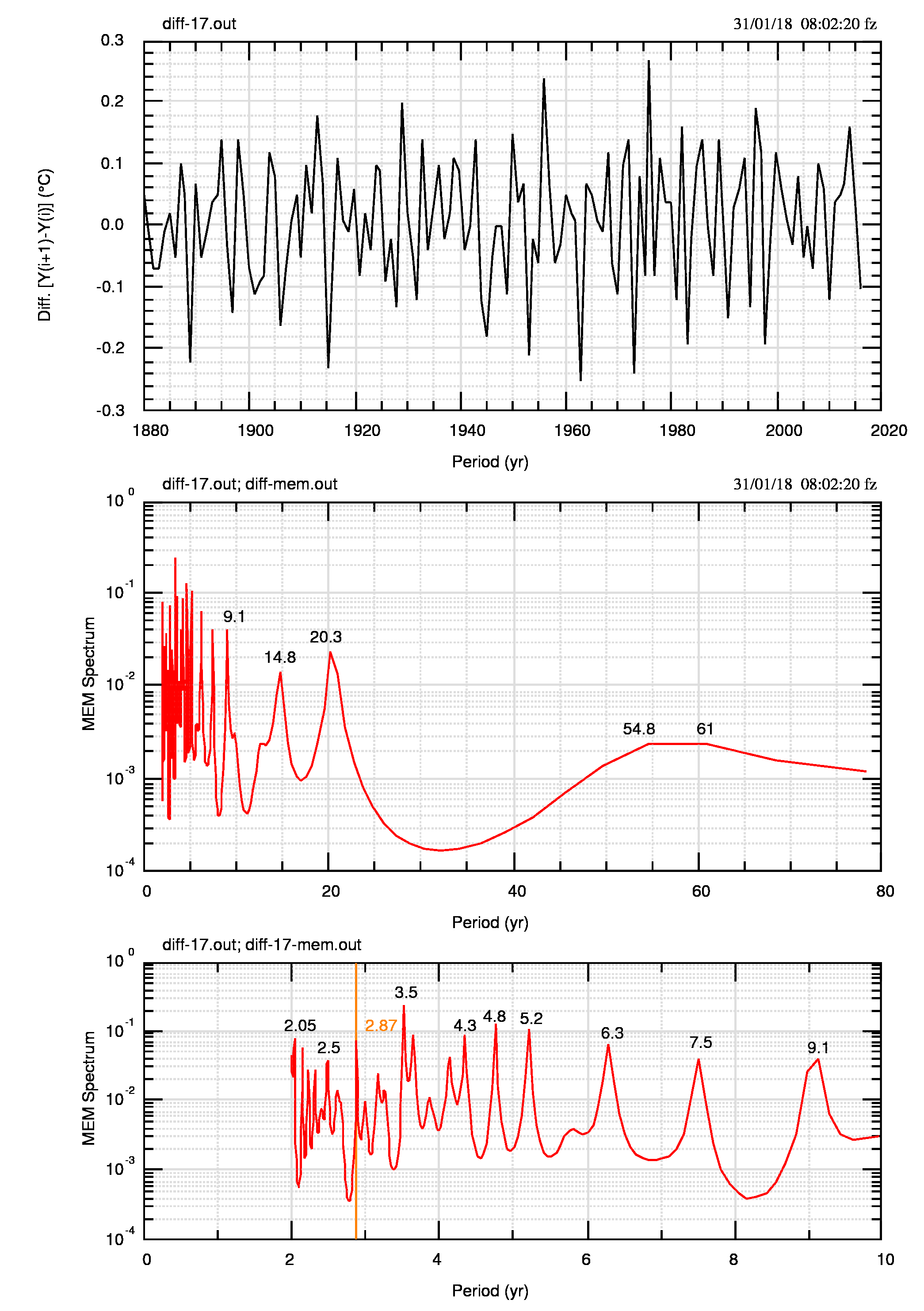
Non avendo potuto dimostrare il caso generale, credo si possa dire che, almeno per le anomalie annuali globali, il fenomeno della persistenza non ha effetti, se non minimi, negli spettri, in particolare sulla posizione dei massimi, cioè sul loro periodo. Questa caratteristica dovrà essere dimostrata (empiricamente) per ogni serie trattata, ad esempio per il livello del lago Vittoria e per i dati mensili NOAA.

Credo che questo articolo stia diventando troppo lungo, per cui mostrerò le altre due applicazioni in un post successivo. Il sito di supporto e la bibliografia restano gli stessi

Bibliografia

1. Koutsoyiannis D.: The Hurst phenomenon and fractional Gaussian noise made easy, Hydrological Sciences-Journal-des Sciences Hydrologiques, 47:4, 573-595, 2002. doi:10.1080/02626660209492961
2. Koutsoyiannis D.: Climate change, the Hurst phenomenon, and hydrological statistics , Hydrological Sciences-Journal-des Sciences Hydrologiques, 48:1, 3-24, 2003. S.I. doi:10.1623/hysj.481.3.43481
3. Koutsoyiannis D.: Nonstationarity versus scaling in hydrology , Journal of Hydrology, 324, 239-254, 2006. doi:10.1016/j.jhydrol.2005.09.022