Una polemica tutta danese

La variazione del trend di innalzamento del livello del mare è considerata uno dei principali indicatori del cambiamento climatico di origine antropica ed una buona percentuale dei rischi connessi al cambiamento climatico è ad essa attribuito. Chi ha avuto modo di seguire la cerimonia di apertura delle Olimpiadi di Rio ha potuto rendersi conto che l’innalzamento del livello del mare, oltre all’incremento delle temperature conseguenti alle emissioni di CO₂ di origine antropica, è uno dei corni principali su cui punta l’offensiva mediatica per convincere il grande pubblico della necessità di fare qualcosa e farla in fretta per scongiurare le conseguenze del cambiamento climatico. Il palcoscenico olimpico è stato un’occasione che la pubblicistica mainstream non poteva lasciarsi sfuggire.

L’unico problema è che il grande pubblico non verrà mai a sapere che ciò che viene spacciato per certo, in realtà non lo è. Diciamo che secondo alcuni è vero e secondo altri non lo è. Molto istruttiva, in proposito, una polemica scientifica che ha coinvolto illustri esponenti della comunità scientifica danese: ricercatori del DMI (Danish Meteorological Institute) e dell’Università di Copenhagen sulle pagine della rivista Journal of Coastal Research. Procediamo, però, con ordine.

Nel 2015 J.M. Hansen; T. Aagaard; e  A. Kuijpers, tre ricercatori dell’ dell’Università di Copenhagen, pubblicarono un articolo su  Journal of Coastal Research:

Sea-Level Forcing by Synchronization of 56- and 74-Year Oscillations with the Moon’s Nodal Tide on the Northwest European Shelf (Eastern North Sea to Central Baltic Sea) (da ora Hansen et al.,  2015)

In questo articolo gli autori sostengono che il livello del mare nell’Atlantico del nord è determinato, tra l’altro, dal periodo nodale lunare. Ricordo a me stesso che si definisce asse nodale la retta che unisce i punti di intersezione dell’orbita lunare con il piano dell’eclittica. Nello schema seguente vengono visualizzati i nodi e la linea dei nodi.

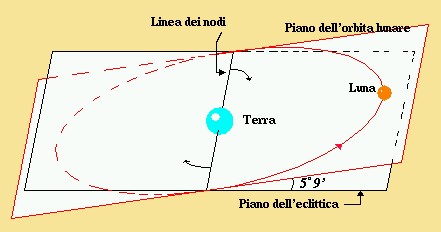
La linea dei nodi non è fissa nello spazio ma si muove nel senso indicato dalle due frecce ed ha un periodo (periodo nodale) di circa 18 anni (18,6 anni, per la precisione).

Applicando l’analisi armonica alle serie di misurazioni di una ventina di mareografi che circondano il Baltico ed altri bacini dell’Atlantico settentrionale e che coprono un periodo di circa 160 anni di osservazioni, Hansen et al., 2015 hanno individuato cinque oscillatori armonici e le relative armoniche (tre principali e due secondarie). Le armoniche principali hanno periodi di 18,6, 60,5, e 76,1 anni. Quelle secondarie hanno periodi di 28,1 e 111,1 anni. E’ appena il caso di notare che il periodo della prima armonica coincide con il periodo nodale lunare e quelli delle altre due armoniche coincidono quasi con il doppio ed il triplo del periodo nodale lunare. I periodi delle armoniche secondarie sono multipli non interi del periodo nodale lunare. Componendo le cinque armoniche mediante un processo di regressione sinusoidale piuttosto complesso, essi sono riusciti a generare una curva teorica che risulta molto somigliante a quella reale: presenta valori dello scarto quadratico medio di circa 2,5 mm e fattore di correlazione di 0,997. Praticamente una fotocopia della curva desunta dalle misurazioni.

L’aspetto più intrigante di Hansen et al., 2015 è che l’armonica con periodo di 60,5 anni corrisponde al periodo dell’Oscillazione Multidecadale Atlantica (AMO) mentre quella con periodo di 76,1 anni secondo gli autori sembrerebbe legata alla NAO o Oscillazione Nord Atlantica. I lettori di CM conoscono bene questi due indici che influenzano il clima dell’emisfero nord terrestre. Personalmente non sono riuscito ad individuare il legame del periodo di 76,1 anni con la NAO, ma secondo gli autori esso è certo.

Tutto questo ha un significato ben preciso in termini pratici. Il livello del mare è determinato da cause naturali e le variazioni della velocità con cui cambia il livello del mare potrebbero essere una conseguenza delle oscillazioni di natura astronomica legate ai periodi lunari.

Qualche mese fa (qui ) su CM esaminai il legame tra AMO e livello del mare e misi in evidenza come le due grandezze fossero correlate in modo piuttosto stretto. Hansen et al., 2015 fornisce un ulteriore conferma di questo legame e evidenzia come la causa ultima di tutto ciò possa essere il periodo nodale lunare che influenza le oscillazioni a frequenza decadale e multidecadale del livello del mare ed anche di AMO (meno chiaramente di NAO). Quando in campo climatologico si introduce una variabilità naturale che contraddice la narrazione corrente del clima che varia solo per colpa dell’uomo, immediatamente si corre a fare le pulci all’articolo che va controcorrente o che potrebbe incrinare le certezze del paradigma dominante. Anche in questo caso è successa la stessa cosa e dopo qualche mese la stessa rivista che aveva ospitato Hansen et al., 2015, ha dato spazio ad un rebuttal dell’articolo di cui stiamo trattando.

Schmith,P. Thejll, e J.W. Nielsen ricercatori del prestigioso DMI hanno pubblicato l’articolo che segue:

Discussion of Hansen, J.M.; Aagaard, T., and Kuijpers, A., 2015. Sea-Level Forcing by Synchronization of 56- and 74-Year Oscillations with the Moon’s Nodal Tide on the Northwest European Shelf (Eastern North Sea to Central Baltic Sea) da ora Schmith et al., 2016.

Schmith et al., 2016 applica l’analisi armonica alle serie di dati studiate da Hansen et al., 2015 e scopre che nessuno spettro di potenza significativa si trova in corrispondenza del periodo nodale lunare. Bisogna precisare che Schmith et al., 2016 ha applicato l’analisi armonica ai dati di Hansen et al., 2015 dopo aver eliminato la tendenza lineare costituita dall’assestamento isostatico post-glaciale (GIA).

La critica metodologica rivolta ad Hansen et al., 2015 è profonda, in quanto questi ultimi avrebbero applicato una procedura di composizione delle armoniche eccessivamente complessa basata sulla regressione sinusoidale (non lineare) invece di applicare la più semplice regressione lineare. Essi avrebbero, inoltre, applicato un procedimento iterativo che avrebbe prodotto un accumulo di errori che rende poco credibili le conclusioni di Hansen et al., 2015.

Concludendo il discorso Schmith et al., 2016 è dell’avviso che i risultati di Hansen e colleghi siano del tutto errati e che le periodicità individuate siano un semplice accidente di calcolo.  In particolare essi hanno trovato un’oscillazione di soli  10 mm in corrispondenza del periodo di 18,6 anni invece dei 70 mm individuati per lo stesso periodo da Hansen e soci. A conferma della bontà della loro analisi i ricercatori fanno notare che tale dato coincide con i risultati dei lavori  di altri ricercatori anche se relativi ad un unico mareografo (quello di Stoccolma).

Ovviamente la ricusazione non è stata accettata in modo supino da Hansen e colleghi che hanno prontamente risposto con un’altro articolo in cui contestano le conclusioni di Schmith et al., 2016 e ribadiscono le conclusioni della loro ricerca del 2015.

Andiamo a vedere, ora, come Hansen e colleghi replicano a Schmith et al., 2016. Per Hansen e colleghi la differenza tra le loro conclusioni e quelle di Schmith e soci va cercata nella diversa metodologia di analisi e nel tipo di studi presi a base della loro ricusazione. I ricercatori fanno notare, inoltre, che i risultati di Hansen et al., 2015 coincidono con le osservazioni mentre quelli di Schmith coincidono con le conclusioni di lavori puramente teorici. Secondo i ricercatori si è dimostrato in più occasioni che i risultati teorici sono sempre sottovalutati rispetto a quelli desunti dalle osservazioni.

Hansen e colleghi contestano alla radice le obiezioni di Schmidt e soci in quanto l’analisi spettrale che hanno applicato è indicata per serie di dati molto lunghe (tra i 220 ed i 300 anni) mentre le serie di dati di cui si dispone sono molto più corte. Altro punto di attrito riguarda l’utilizzo dei metodi di regressione. Hansen et al., 2015 applica una curva di regressione sinusoidale mentre Schmidt et al., 2016 applica una semplice regressione lineare. A giudizio di Hansen e colleghi la loro metodologia consente di calcolare in modo più preciso i residui e di individuare, in tal modo, più armoniche che, composte, generano il dato misurato. I loro calcoli consentono, infine, di appurare che nessun altra armonica, diversa da quelle prese in considerazione, riesce a generare una curva che abbia un coefficiente di correlazione così alto con le curve desunte dalle misurazioni.

Su di un punto Schmith e soci concorda con Hansen e colleghi: non esistono metodiche di calcolo che consentano di accertare l’intervallo di incertezza di modelli basati sulla composizione di cicli per cui si giunge al paradosso che né i risultati di Hansen e colleghi, né quelli di Schmidth e soci sono confutabili in toto.

Per il povero lettore questa è la peggiore delle conclusioni in quanto non consente di dirimere la questione e tutto resta in alto mare: tra l’altro siamo perfettamente in tema! 🙂

Ad onor del vero alcune delle considerazioni finali svolte da Hansen e colleghi nella loro replica mi hanno fatto propendere, anche se con molta cautela e diversi distinguo, verso i loro risultati:

“Residui minori non possono essere prodotti aggiungendo un sesto oscillatore nell’intervallo di periodi tra 18,6 e 160 anni. Residui più grandi vengono prodotti a seguito della  rimozione  di uno dei cinque oscillatori seguita dalla modulazione dei rimanenti quattro oscillatori o per ulteriore modulazione dei parametri che caratterizzano le  cinque oscillazioni. Considerare  modulazioni polinomiali del secondo e  terzo ordine con accelerazioni superiori a 0,0004 millimetri/y² della tendenza generale di 1,18 mm/y comporta la produzione di residui più grandi. … la curva ricostruita in Figura 1 (pannello inferiore) non può essere prodotta da un diverso insieme di oscillatori (numero di oscillatori e diversi parametri di oscillazione) senza produrre residui più grandi. Il nostro metodo non è in grado di (i) individuare oscillazioni più piccole del più piccolo oscillatore parametrico identificato ( es. 8 mm, t-b), (ii) distinguere le tendenze generali da eventuali oscillatori che sono più lunghi rispetto alla serie temporale  a disposizione ( es. 160 y), (iii) individuare modifiche dei parametri di una tendenza generale oltre il periodo di ripetizione degli oscillatori considerati”

Come già accennato né Hansen et al., 2015, né Schmith et al., 2016 riescono ad essere pienamente convincenti in quanto entrambe le ricerche presentano punti in ombra. Nel caso di Hansen e colleghi lascia un po’ a desiderare la molteplicità dei parametri numerici in gioco che, però, produce risultati coerenti con le osservazioni. Resta da vedere se tale coerenza reggerà anche per il futuro o si renderà necessario modificare i parametri numerici delle armoniche considerate.

Nel caso di Schmith e soci lascia a desiderare la scarsa coerenza delle loro conclusioni con le osservazioni anche se molte delle obiezioni sollevate non mi sembra che siano peregrine.

Solo il tempo potrà dirci chi aveva ragione e chi torto: non resta che aspettare. La scienza del clima non è definita, a quanto pare.