La differenza tra clima e tempo meteorologico è fondata sul fatto che il tempo meteorologico è caotico il clima non lo è. Questo è quanto recita la vulgata e su questo assunto si basa la pretesa di poter prevedere lo stato del clima a distanza di decenni se non secoli. Ad essere sinceri i climatologi non pensano minimamente a prevedere in modo rigoroso il clima, possono al massimo prevedere la tendenza del clima, ovvero cosa potrà succedere nel futuro entro un certo margine di incertezza. Il problema è l’ideologia che si innesta su tutto ciò e trasforma la previsione di un trend entro un certo margine di incertezza in una certezza assoluta.
Il sistema climatico, a mio giudizio è un sistema dinamico complesso non lineare caotico a dimensione frattale: lo scrissi tempo addietro in questo articolo pubblicato su CM.
Scorrendo le news dell’ANSA la mia attenzione è stata attratta dall’immagine di un frattale. Aperta la news non è stato difficile arrivare alla fonte. Si tratta di un articolo a firma di Zhi-Gang Shao e Peter D. Ditlevsen pubblicato su Nature Communications:
Contrasting scaling properties of interglacial and glacial climates da ora Shao et al., 2016.
Il titolo non rende l’idea, ma il senso dell’articolo è tale da farmi fare un salto sulla sedia: le conclusioni sono molto simili a quelle cui ero giunto io, ma fondate su dati quantitativi e non, come nel mio caso, su speculazioni qualitative. Nell’articolo si sostiene, infatti, che il clima terrestre ha dimensione frattale e ciò comporta che è caotico quasi come il tempo meteorologico. E’ una conclusione piuttosto forte che bisogna approfondire bene e così ho cominciato a studiare: gli esiti dello studio sono costituiti da questo post.
Shao et al., 2016 parte dalla considerazione che il clima terrestre è frutto di profonde e complesse interazioni tra atmosfera, idrosfera, criosfera e, ovviamente, biosfera. Le interazioni anzidette determinano un comportamento non lineare del sistema climatico terrestre. Tale sistema è stabilizzato nello spazio delle fasi da un attrattore che, secondo me è strano, secondo altri non lo è. Scopo di Shao et al., 2016 è quello di individuare nei registri dei dati osservativi dei parametri che caratterizzino il clima terrestre, delle strutture che rappresentino degli invarianti di scala. Detto in altri termini ci si propone di individuare una struttura frattale della serie di temperature, per esempio, in modo da trovare la firma di un sistema dinamico non lineare caotico. Allo scopo di rendere più chiaro il discorso di Shao et al., 2016 è opportuno delineare un quadro storico-analitico che, chi vuole, può tranquillamente saltare, passando direttamente alle considerazioni su Shao et al., 2016..
Inquadramento storico-analitico (può essere saltato)
Nel 1951 H.E. Hurst effettuò una serie di studi sulla capacità di immagazzinamento e di deflusso di un invaso sul fiume Nilo. Egli si proponeva di individuare un’altezza dello sbarramento tale da far si che nell’invaso non si trovasse né una quantità d’acqua troppo ridotta, né una quantità d’acqua eccessiva. In un invaso ci si trova, normalmente, di fronte ad una portata d’acqua in ingresso e ad una portata d’acqua in uscita. Essendo la portata uscente costante o variabile entro limiti molto ristretti, mentre quella entrante variabile, appare ovvio che bisogna stabilire la corretta altezza della diga in modo tale che essa riesca a contenere la giusta quantità d’acqua e che tale quantità non sia eccessivamente variabile (idealmente dovrebbe essere costante). Il problema reale è, quindi, quello di appurare una legge di variazione della portata in ingresso in quanto essa dipende da una lunga serie di fattori legati al clima, alla struttura del bacino fluviale, alla natura dei terreni, alla loro morfologia etc. Hurst analizzò la lunga storia delle inondazioni del Nilo, registrata accuratamente dalla schiera di idrologi che si è succeduta nel corso della storia e notò che a piene violente succedevano piene intense e viceversa, a piene di debole intensità succedevano piene deboli. Lo schema si ripeteva, inoltre, in maniera pseudo-periodica, nel senso che si riuscivano ad individuare dei “blocchi” che si ripetevano nel tempo. Applicando alle serie di dati in suo possesso le analisi statistiche convenzionali, non si riuscivano ad individuare delle strutture definite, per cui le intensità delle piene apparivano casuali.
Anni prima A. Einstein studiando il moto browniano, riuscì a stabilire che il cammino medio di una particella che si muove in modo casuale o browniano (R) è una funzione della radice quadrata del tempo (t):
R= k(t1/2)
ove k è una costante.
Hurst generalizzò questa relazione che divenne
R/S=k(tH)
In questa formula R è l’ampiezza di un intervallo di valori di una serie temporale (range), S è la deviazione standard, t il tempo espresso come successione di numeri reali ed H è l’esponente di Hurst.
A seconda del valore che assume H si possono avere tre famiglie di fenomeni:
- H=1/2 comporta che il fenomeno che si sta considerando è assimilabile al moto browniano e, cioè, casuale;
- 0≤H<1/2 comporta che il fenomeno che si sta considerando è caratterizzato da un’alternanza di fasi opposte: ad una positiva ne segue una negativa e così via per tutta l’ampiezza dell’intervallo temporale che si sta considerando;
- 1/2<H≤1 comporta che il fenomeno è di tipo “persistente”.
Qualora la relazione di Hurst venga rappresentata in un diagramma logaritmico/logaritmico si vede che ci si trova di fronte ad una retta la cui pendenza è proprio l’indice di Hurst.
log(R/S)=logk+Hlogt
In un fenomeno persistente si verificano degli pseudo-cicli: le grandezze considerate si succedono nel tempo in modo “regolare” nel senso che a valori elevati seguono valori elevati ed a valori bassi, succedono valori bassi. Un esempio aneddotico è costituito dal racconto biblico delle sette vacche magre e delle sette vacche grasse che furono interpretate da Giuseppe come sette anni di abbondanza cui sarebbero seguiti sette anni di carestia. Tradotto in altri termini significa che a sette anni di piena del Nilo abbondante, sarebbero succeduti sette anni di piene scarse e, quindi, sette anni di carestia. Nel caso delle piene del Nilo Hurst calcolò per l’indice H il valore 0,9. Possiamo affermare, pertanto, che un fenomeno apparentemente caotico come il succedersi delle piene del Nilo non è regolato dal caso, (H=1/2), ma ha una struttura cioè presenta dei cicli o pseudo cicli.
Anche i fenomeni meteorologici sono di questo tipo in quanto è molto probabile che a giornate calde seguano giornate calde mentre è meno probabile che ad una giornata calda segua una giornata fredda e viceversa. Un esempio ulteriore potrebbe essere costituito dalle condizioni di blocco che sovente si determinano nell’atmosfera e condizionano il tempo per giorni e giorni, se non per mesi.
E con questo siamo entrati a pie’ pari nel campo delle dimensioni frattali indagate da Mandelbrott ed altri nel corso della seconda metà del 20° secolo.
Aristotele nel libro delta della Metafisica (quello delle definizioni) definì la dimensione:
“In tutti i casi, però, l’uno è indivisibile o per la quantità oppure per la specie. Orbene, ciò che è indivisibile secondo la quantità e in quanto quantità, e che è indivisibile in tutte le dimensioni e non ha posizione, si chiama unità; invece, ciò che è indivisibile in tutte le dimensioni ma ha una posizione, si chiama punto ciò che è divisibile secondo una sola dimensione si chiama linea, mentre ciò che è divisibile secondo due dimensioni si chiama superficie e, infine, ciò che è divisibile secondo la quantità in tutte e tre le dimensioni si chiama corpo.”
Si tratta della classica definizione di strutture adimensionali, monodimensionali e pluridimensionali. Questi concetti sono stati la base della geometria euclidea per secoli e divennero fondamentali a partire dal 1600 con Galilei e Newton: essi basarono tutta la fisica sulla Meccanica che è coerente solo in un sistema euclideo in cui, cioè, le dimensioni sono espresse da numeri interi.
Negli anni ’80 del 20° secolo B. Mandelbrot criticò profondamente la rigidità della geometria euclidea in quanto incapace di rappresentare la complessità della Natura:
“Le nubi non sono sfere, le montagne non sono coni, le coste non sono cerchi…..Io sostengo che molte forme in Natura sono così irregolari e frammentate che, in confronto a Euclide…..la Natura esibisce non solo un più alto grado, ma anche un diverso livello di complessità”
(The Fractal Geometry of Nature – B. Mandelbrot, 1982)
La geometria frattale è la geometria delle coste, delle nuvole, dei sistemi complessi, in ultima analisi.
Per poter rappresentare la complessità delle forme naturali, Mandelbrot introdusse il concetto di “dimensione frattale” (da fractus, cioè rotto) che è piuttosto complessa in quanto coinvolge concetti topologici che non è il caso di indagare in questa sede. Basti solo dire che un oggetto ha dimensione frattale quando, per dirla con Mandelbrot “la sua dimensione di Hausdorff-Besicovitch eccede strettamente la sua dimensione topologica: Dt<D“.
I lavori pionieristici di Hurst e Mandelbrot sono fortemente interconnessi in quanto indagano la stessa cosa: fenomeni complessi che, apparentemente, sono privi di “forma” cioè di regolarità. Nella pratica comune il concetto di dimensione frattale si applica tanto ad oggetti (le coste, le nuvole, l’albero bronchiale e via cantando), tanto a serie temporali (le piene del Nilo, le serie di temperature, il battito cardiaco e così via).
A prima vista potrebbe apparire strano applicare ad una serie di dati un approccio geometrico come quello frattale, ma la contraddizione è solo apparente. Analizzando la relazione che intercorre tra la deformazione di una molla e la forza che la determina, è facile vedere che ci si trova di fronte ad una funzione lineare, cioè una retta. Noi modelliamo la relazione tra due insiemi di dati mediante un elemento geometrico euclideo monodimensionale: la retta. Avendo introdotto la dimensione frattale, non deve stupirci il fatto che una serie temporale possa essere rappresentata da un frattale, cioè una figura geometrica con dimensione frattale (è solo il caso di precisare che esistono frattali con dimensione intera come ad esempio la curva di Hilbert, ma che alla luce della definizione di Mandelbrot sono frattali).
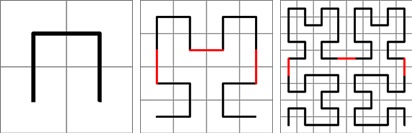
La relazione determinata empiricamente da Hurst rappresenta un esempio di relazione frattale e l’esponente H di Hurst rappresenta il grado di correlazione degli elementi della serie temporale.
Aspetti salienti di Shao et al., 2016
Tralasciando per brevità ulteriori aspetti analitici, torniamo a Shao et al., 2016. L’articolo rappresenta, in buona sostanza, il tentativo di determinare il valore dell’esponente di Hurst per alcune serie temporali molto note a chi si occupa di climatologia. Nell’ambito della ricerca climatologica si è dibattuto a lungo circa la natura del sistema climatico: si tratta di un sistema a dimensione frattale e, se sì, a dimensione monofrattale o multifrattale?
La risposta è estremamente importante in quanto se esso non ha dimensioni frattali ha senso poter escludere che le condizioni iniziali non sono in grado di determinare la sua evoluzione futura per cui siamo in grado di determinarne le tendenze future tramite modelli più o meno complessi o ensemble di modelli. La climatologia attuale è basata su questa ipotesi: esistono delle forzanti interne ed esterne che attraverso azioni e retro-azioni riescono a determinare il clima terrestre e che non dipendono dalle condizioni iniziali. Ciò non accade per il tempo atmosferico che, invece, non può essere previsto a grandi distanze di tempo in quanto fortemente sensibile alle condizioni iniziali. Sulla scorta di questo presupposto sono plausibili gli scenari delineati dai climatologi.
Il discorso cambia se il sistema climatico ha dimensioni frattali: in questo caso anche il sistema climatico diventa sensibile alle condizioni iniziali come il tempo meteorologico ed ha poco senso parlare di prevedibilità a lungo termine, anche a livello di semplice tendenza. Ammesso che il sistema climatico abbia dimensione frattale esso può essere di tipo monofrattale o multifrattale.
Qualora il sistema climatico sia di tipo monofrattale, la sua struttura è indipendente dalla scala per cui tende a ripetersi sempre uguale a se stessa indipendentemente dalla durata dell’intervallo temporale utilizzato. In questo caso si parla di invarianza di scala come, ad esempio, nel caso di oggetti reali (struttura dell’albero bronchiale o del cavolfiore, per esempio) o, per restare nel campo analitico, di curve particolari come la curva di Koch.
Nell’ipotesi in cui esso si configura come un sistema multifrattale le caratteristiche che lo determinano non si presentano sempre allo stesso modo al variare della scala temporale utilizzata, ma cambiano al cambiare del fattore di scala. Un esempio può essere costituito dai mercati finanziari che hanno comportamenti differenti a seconda dell’intervallo temporale a cui vengono analizzati.
Shao et al., 2016 ha analizzato diverse serie di temperature: quella strumentale che copre gli ultimi 150 anni, quella desunta dai dati di prossimità della carota di ghiaccio groenlandese NGRIP che copre gli ultimi 120000 anni, quella derivata dalla carota antartica DOME C che si estende fino ad 800000 anni fa e, infine, quella derivata dall’analisi dei foraminiferi contenuti in una carota costituita dai sedimenti dell’oceano profondo e che fornisce indicazioni sulla temperatura degli oceani e sul volume dei ghiacci a loro volta proxi della temperatura globale.
Assumendo come termine di paragone la serie delle temperature strumentali, esse sono state confrontate con quelle degli ultimi 10000 anni (Olocene) e, successivamente, con quelle degli altri periodi temporali presi in considerazione. Nel grafico che segue tratto da Shao et al., 2016 sono chiaramente visibili le serie di temperature prese in considerazione.
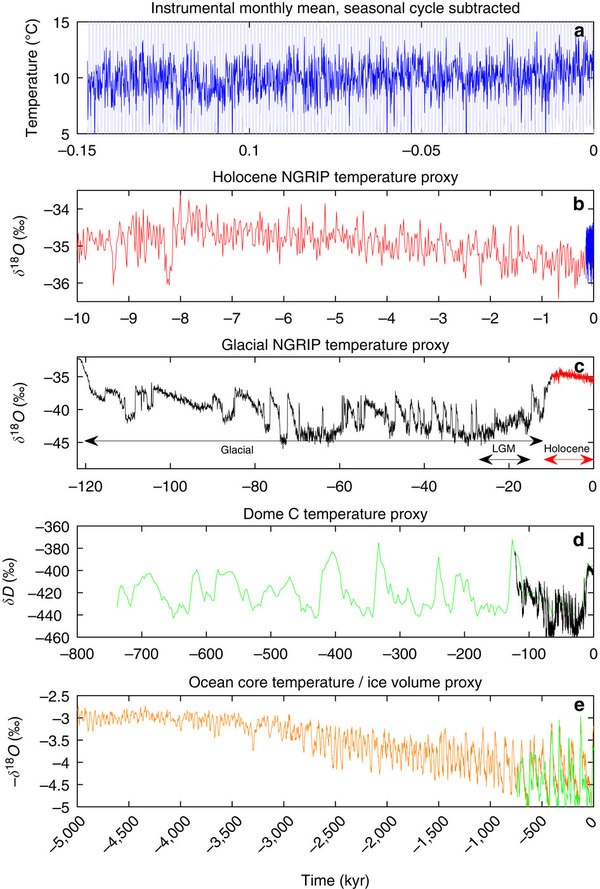
Un semplice confronto visivo consente di individuare una netta differenza tra il clima olocenico e quello glaciale che lo ha preceduto. Il clima dell’Olocene, desunto dalla temperatura globale, si presenta piuttosto simile a se stesso indifferentemente dalla scala temporale a cui lo si guarda. Diverso è il caso del clima glaciale che presenta forma diversa a seconda della scala temporale utilizzata. Da questa semplice considerazione possiamo concludere che il clima olocenico è di tipo monofrattale, quello glaciale di tipo multifrattale.
Questa conclusione è la stessa a cui giunge Shao et al., 2016. Le conclusioni degli autori non sono state desunte, ovviamente, da una semplice osservazione, ma da una rigorosa analisi matematica che cercherò di sintetizzare nel miglior modo possibile.
L’analisi dei dati è stata condotta mediante strumenti analitici particolarmente potenti. In presenza di serie fortemente non stazionarie come quelle climatiche il coefficiente di Hurst può essere determinato mediante la Detrended Fluctuation Analysis (DFA). Essa è una metodologia che consente di calcolare una Funzione di fluttuazione [F(n)] in cui “n” rappresenta il numero di finestre in cui è stata scomposta la serie temporale originaria (Xi). Trascurando i dettagli analitici, alla fine otterremo una funzione di “n” che in un diagramma log/log consente di determinare la pendenza della retta risultante che rappresenta l’esponente di Hurst (H) e, quindi, appurare se la serie numerica ha carattere aleatorio o ha una qualche struttura. A seconda dei valori che assume tale esponente, possiamo trovarci di fronte a varie situazioni:
- H = 0.5 per serie Xi casuali (rumore gaussiano)
- H = 1.5 per serie Xi tipo rumore browniano
- H = 1 per serie con spettro a legge di potenza del tipo 1/f
- 5< H <=1 per serie con persistenza
- 0< H <0.5 per serie antipersistenti
- H >1 per serie con correlazione, ma non frattali
Applicando tale metodologia di analisi alle serie di temperature prese in esame, Shao et al., 2016 hanno potuto accertare per il periodo olocenico un valore di H = 0,7 circa. Sulla scorta della precedente elencazione ci troviamo di fronte ad una serie con persistenza, ovvero ad un sistema caratterizzato da geometria monofrattale per cui la struttura della serie è indipendente dalla scala temporale considerata.
La stessa tecnica di analisi applicata al periodo glaciale precedente l’Olocene, ha consentito di individuare valori di H maggiori di 1 e quindi dobbiamo concludere che il periodo glaciale nel suo complesso non è monofrattale. Indagini relative ai diversi interglaciali contenuti nelle serie di temperatura, infine, hanno consentito di appurare che durante gli interglaciali le serie numeriche di temperatura hanno struttura monofrattale (H = 0,7 circa) mentre ciò non accade durante i periodi glaciali.
La conclusione logica di tutto il discorso è che il sistema climatico è un sistema dinamico non lineare con struttura multifrattale nei periodi glaciali, monofrattale durante gli interglaciali come quello attuale. Questo fatto consente di spiegare alcune “stranezze” dei periodi glaciali che, invece, non compaiono durante gli interglaciali se non in modo estremamente raro. Mi riferisco ai cosiddetti interstadiali o eventi di Dansgaard-Oeschger (DO) che sono dei periodi relativamente brevi (durate minori di 10000 anni, in genere) caratterizzati da temperature molto più alte di quelle medie del periodo glaciale. Essi si differenziano di periodi interglaciali perché questi ultimi durano ben oltre i 10000 anni.
I climatologi si sono a lungo interrogati sulla natura di questi eventi spettacolari per intensità e durata avanzando svariate ipotesi. In un sistema climatico multifrattale essi si inquadrerebbero come dei fenomeni indotti dalla variabilità interna del sistema. In base a questo nuovo modello l’inizio e la fine di un periodo glaciale sarebbero conseguenza di forzature esterne di natura orbitale (cicli di Milankovich) che vanno ad alterare i parametri relativi all’insolazione del pianeta Terra, mentre gli interstadiali sarebbero eventi legati alla variabilità interna del sistema e, quindi, indipendenti da forzature esterne.
Sorge spontanea, a questo punto, una domanda: a cosa è dovuta la forte instabilità dei periodi glaciali rispetto agli interglaciali? Shao et al., 2016 non forniscono una risposta esaustiva alla questione. A loro giudizio tali eventi sono innescati dalle fluttuazioni interne della circolazione rovesciata dell’Atlantico meridionale (AMOC). Nei periodi interglaciali tali fluttuazioni non sarebbero in grado di innescare eventi interstadiali a causa dell’assenza delle immense coltri glaciali presenti nei periodi glaciali.
Nell’articolo originale sono presenti ulteriori interessantissimi dettagli sia a livello analitico (i vari test cui sono state sottoposte le ipotesi formulate dai ricercatori, per esempio) e molte altre considerazioni circa la struttura del sistema climatico terrestre, ma, secondo me, la cose più rilevanti sono quelle che ho riportato nel post.
Delle conseguenze circa la prevedibilità del comportamento del sistema climatico terrestre ho già detto, ma non è solo questa l’unica conseguenza dello studio. In linea di massima possiamo pensare, infatti, che essendo quello climatico un sistema a dimensione frattale fortemente non lineare, forse sarebbe opportuno invertire la tendenza attuale passando dal globale al locale. Nei sistemi frattali è possibile, infatti, individuare degli invarianti di scala che si ripetono regolarmente dal livello locale fino a quello più generale. Non si può cogliere, per esempio, il meccanismo della respirazione se non si indaga il comportamento microscopico del sistema polmonare, se cioè non si va a vedere ciò che succede a livello dei rami più periferici dell’albero bronchiale. Allo stesso modo è impossibile capire come evolve il sistema climatico globale se non si conosce cosa accade a livello regionale.
Un bel cambio di paradigma, non c’è che dire.


“…misconoscere un problema di “rischio climatico”, esattamente come esiste il rischio idrogeologico…”
Non “Esattamente” caro Fabio.
Del rischio idrogeologico etc sappiamo abbastanza, perché abbiamo esperienza, teoria e pratica che si confortano a vicenda.
Del rischio climatico sappiamo poco o nulla dell’effetto antropico, abbiamo poca esperienza, molta teoria modellistica che poco si adatta all’osservazione della realtà e zero pratica ( leggi contromisure efficaci).
Per quello che vedo la scienza del clima non è scienza, ma solo un modo per ottenere dei cambiamenti sociali con ridistribuzione della ricchezza e del potere. Il fatto che molti la dichiarino settled nonostante le lacune citate in precedenza ne è una prova lampante.
Il principio di precauzione è in quest’ottica usato come i terroristi usano gli scudi umani.
Cordiali saluti.
Grazie Donato per le sempre interessanti risposte al mio commento. Certamente anch’io noto diverse affinità tra il sistema climatico e il sistema finanziario, soprattutto in termini di complessità del sistema e di conseguenza in termini di metodologia di approccio. Sistemi peraltro certamente molto resistenti alla modellazione fisico-matematica. Poi da qui a dire che per tali sistemi si possa riconoscere una natura frattale, questo non lo so, istintivamente non mi viene naturale pensarlo, ma essendo consapevole della mia ignoranza sull’aspetto teorico-strutturale di frattale o dimensione frattale, mi astengo da ulteriori analisi in merito. Riguardo la tua conclusione finale sulla presunta predicibilità del clima futuro e conseguenti policy devo dirti che detta così la sottoscrivo in pieno. Tuttavia, e in questo forse intravedo le differenze sostanziali del nostro pensiero, io tendo a leggere la problematica in maniera diversa. Io non credo che sia la vera scienza del clima ad esprimersi in questi termini, ma soltanto la sua versione mediatizzata o quella piccola parte di derivazione ideologica e/o speculativa. Credo invece che la vera ricerca scientifica in campo climatologico, così come quella di molti altri campi come ad esempio quella medica, sia perfettamente cosciente dei propri limiti, sia teorici che sperimentali e non lo nasconda. Io credo che la vera scienza del clima non si proclami assolutamente “settled”, nè sputi sentenze dogmatiche, anche se poi la ricerca è ricerca e le evidenze scientifiche sono evidenze scientifiche, è ovvio che poi non possiamo prescindere da questo. Tuttavia credo che, comunque la si pensi, non si possa (per come la vedo io) misconoscere un problema di “rischio climatico”, esattamente come esiste il rischio idrogeologico, il rischio sanitario, il rischio sismico, il rischio ambientale ecc. E riguardo il “principio di precauzione”, non ci vedo nulla di male, anzi, lo mettiamo in pratica tutti costantemente nel nostro quotidiano (senza prendere in considerazione i pur numerosi incoscienti) quando non fumiamo per non aumentare il rischio di cancro al polmone, non beviamo prima di metterci alla guida, mettiamo le cinture prima di avviare il motore della nostra auto, evitiamo di mangiare troppi dolci o troppa carne conservata per non aumentare oltre che di peso, il rischio di tumore al colon, cerchiamo di proteggere i nostri figli in tenera età. Si potrebbero fare decine di altri esempi di “principio di precauzione” legati alla scienza o al vivere quotidiano. Mi chiedo, perché allora due pesi e due misure? La scienza dei cambiamenti climatici non è scienza? Spero di non essere andato OT.
Fabio
[…] storico-analitico (può essere saltato oppure letto QUI […]
Pezzo indubbiamente molto interessante e con un grado piuttosto elevato di difficoltà interpretativa direi, almeno per me. Complimenti Donato. Devo dire che l’argomento mi interessa molto e quindi tento di intervenire sulla questione. Bene, sul fatto che il clima sia un sistema complesso e non lineare penso che oramai non sussistano più dubbi. Aggiungerei, però, per evitare fraintendimenti, che il termine “complesso” nella scienza ha un significato ben preciso e diverso dal confondente aggettivo apparentemente surrogato di “complicato”. Lo studio dei sistemi complessi sinteticamente, è lo studio dei processi collettivi che presentano emergenza. Pertanto io credo che quando si abbia a che fare con un sistema complesso vero, il clima, un essere vivente, i processi cognitivi, le crisi finanziarie, le aziende, urge fare un salto concettuale e cominciare anche a diffidare dell’approccio squisitamente fisico-matematico come unica soluzione pensando invece a quale possa essere concretamente la strategia metodologica più efficace. Non so se il caso dell’invaso sul fiume Nilo possa essere annoverato tra i sistemi complessi propriamente detti. Non è possibile infatti descrivere un sistema complesso con un unico modello formale, ma servono necessariamente più modelli e più approcci. Io credo che anche la differenza sostanziale tra clima e tempo abbia a che fare in fondo anche con il tipo di approccio che scegliamo per studiare il sistema, prevalentemente statistico nel primo caso e prevalentemente deterministico nel secondo. Non conosco bene la matematica della teoria dei frattali e quindi non entro nel merito, però devo dire che sulla natura frattale del clima continuo a conservare qualche dubbio. Se un sistema complesso infatti si caratterizza per il fenomeno dell’emergenza, possiamo però anche distinguere ulteriormente tra emergenza computazionale ed emergenza intrinseca. Nella prima tipologia rientrano i sistemi caotici, caratterizzati da una complessità algoritmica se vogliamo, impredicibili sì, ma perché fortemente influenzati dalle condizioni iniziali e quindi legati ad una sorta di perdita di memoria durante l’evoluzione dinamica, es. automi cellulari, frattali ecc. Nella seconda invece rientrano la stragrande maggioranza dei fenomeni naturali (quelli citati precedentemente e anche il clima), caratterizzati da una continua rottura di simmetria (anche in seguito a eventi casuali) e conseguente continua riorganizzazione dei rapporti sistema-ambiente. Pertanto, secondo questa interpretazione, sostenuta oltre che da me anche da alcuni importanti fisici teorici ed epistemologi, inquadrare il clima nella casella di un sistema frattale potrebbe sembrare un po’ una forzatura concettuale. Ma Donato, prendila così, come un’ulteriore, possibile riflessione su una questione tanto complessa quanto affascinante. Complimenti ancora per l’elevato profilo del tuo pezzo.
Fabio
Fabio ti ringrazio per le belle parole e soprattutto per le interessanti considerazioni che, come al solito, invitano ad una maggiore ed ulteriore riflessione.
.
Tu scrivi: “Pertanto io credo che quando si abbia a che fare con un sistema complesso vero, il clima, un essere vivente, i processi cognitivi, le crisi finanziarie, le aziende, urge fare un salto concettuale e cominciare anche a diffidare dell’approccio squisitamente fisico-matematico come unica soluzione pensando invece a quale possa essere concretamente la strategia metodologica più efficace.”
Non posso che concordare, ma se da un’analisi statistica come quella di Shao et al., 2016 emergono delle caratteristiche generali del sistema che possono essere espresse in termini fisico-matematici, io ne sono felice. L’aspetto interessante di questo articolo, almeno per me, è che il sistema climatico ha molto in comune con sistemi come quello finanziario, per esempio.
E quello finanziario è un sistema a dimensione multifrattale, c’è poco da fare. La dimostrazione della verisimiglianza dei due sistemi è costituita dal fatto che molte delle tecniche di indagine statistica utilizzate per studiare il clima terrestre, sono mutuate dall’econometria (ad esempio la causalità di Granger per problemi di attribuzione). Questo dal punto di vista del quadro generale. Dal punto di vista particolare non posso che convenire con te che gli strumenti matematici di cui disponiamo sono inadeguati a prevedere il comportamento di sistemi dinamici complessi come quello climatico o quello finanziario.
.
Circa la dipendenza o meno dalle condizioni iniziali io sono un po’ più possibilista di te. Le grandezze che caratterizzano il sistema climatico, temperatura per esempio, sono autocorrelate nel senso che le temperature di ieri influenzano quelle di oggi e anche quelle di domani. Nella visione classica il “ricordo” delle condizioni di partenza si perde dopo qualche giorno ed il sistema diventa impredicibile (previsioni meteo). Come tu fai notare, in questa ottica il sistema climatico non può essere assimilato ad un sistema caotico, ma ad un sistema in cui è possibile che in qualunque istante si verifichi la rottura della simmetria facendolo scivolare verso condizioni di equilibrio differenti. Su questo punto non mi sento di condividere del tutto la tua posizione (sono in minoranza, lo so, ma la cosa è relativa) e propendo per un sistema climatico piuttosto sensibile a quelle che sono le condizioni iniziali, quindi piuttosto caotico.
Come tu ben sai sono anni che sostengo questa tesi ed il lavoro di Shao mi conforta. Ciò non toglie che io possa sopravvalutare i risultati esposti nell’articolo: Kuhn docet! 🙂
.
Dovrai convenire con me, infine, che la linea di pensiero dominante è quella per cui il clima del futuro è prevedibile di qui a un secolo e passa e questa, permettimi la franchezza, è una cavolata colossale, indipendentemente dai frattali ed annessi e connessi. Così come è poco scientifico scrivere che la scienza del clima è settled: non mi sembra che siano solo i dettagli quelli da definire.
Eppure noi dobbiamo sottostare ad una serie di imposizioni e limitazioni che vengono imposte sulla base di queste assunzioni di principio e sulla base del fatto che in Europa il cosiddetto “principio di precauzione” vale più della legge di Newton.
.
Parafrasando il titolo di un noto film, non ci resta che … attendere (ulteriori sviluppi, ovviamente).
Ciao, Donato.
Caro Donato, bel post e scritto in modo tale da far capire anche a me argomenti che non conosco e che non sono affatto semplici, anche se gli autori dichiarano che le loro tecniche sono facilmente implementabili.
E’ molto intere3ssante la possibilità, illustrata nella fig.2 dell’articolo, di definire un parametro, H, non solo diverso tra Olocene e Glaciale ma anche in grado di rappresentare (nell’Olocene) intervalli che vanno da giorni a millenni.
Anche la possibilità di definire gli eventi DO come parte della variabilità intrinseca dei periodi glaciali, e non generati da fattori esterni, è importante. La causa che innescherebbe questi eventi -AMOC- non ti sembra una spiegazione soddisfacente: però l’essere riusciti a collocare la loro presenza in certi periodi e non in altri è, per me, un passo avanti e qualcuno, prima o poi troverà una spiegazione migliore-AMOC- non ti sembra una spiegazione soddisfacente: però l’essere riusciti a collocare la loro presenza in certi periodi e non in altri è, per me, un passo avanti e qualcuno, prima o poi troverà una spiegazione migliore.
Sono curioso di seguire gli sviluppi di questa metodologia e, se ce ne saranno, di leggere i tuoi prossimi post sull’argomento.
Ciao. Franco .
Sono curioso di seguire gli sviluppi di questa metodologia e, se ce ne saranno, di leggere i tuoi prossimi post sull’argomento.
Ciao. Franco
Chiedo scusa: ho avuto qualche problema con il copia-incolla.
Franco
Caro Franco, credo che tu abbia centrato il “core” del problema: l’attribuzione degli eventi di DO alla variabilità interna di un sistema dinamico a dimensione multifrattale. L’AMOC può essere una delle cause scatenanti dell’evento, ma non è rilevante. Come tu hai giustamente puntualizzato, le cause possono essere anche altre, ma l’aspetto importante è che tali fenomeni sono tipici di sistemi dinamici a dimensione multifrattale e non di altri.
Lo studio mi è sembrato importante proprio per questi aspetti che travalicano il singolo o i singoli eventi e che coinvolgono il sistema nel suo complesso. .
Come avrai avuto modo di constatare leggendo l’articolo, l’aspetto veramente affascinante di tutta la questione è l’enorme complessità del sistema climatico terrestre. Un sistema che oscilla tra condizioni apparentemente estreme, ma che rientrano in un’unica cornice fisico-matematica. Un sistema che presenta strutture estremamente complesse a scale diurne, mensili, annue, decadali, multidecadali, secolari, millenarie e multimillenarie, eppure un unico sistema che ripresenta situazioni sempre simili a quelle già verificatesi nel passato e che, probabilmente, si ripresenteranno anche nel futuro.
In tutto ciò possiamo essere certi che l’Olocene finirà e sarà sostituito da un nuovo periodo glaciale che metterà a durissima prova la nostra civiltà (qualora esistesse ancora 🙂 ) con i suoi bravi interstadiali che allevieranno la cappa del freddo. Non sappiamo quando, ma sicuramente accadrà. Ce lo garantisce la struttura frattale del sistema climatico terrestre come emerge dalla storia geologica della Terra.
Ciao, Donato.