Grazie ad una segnalazione dell’amico Max Pagano ho avuto modo di leggere un interessantissimo articolo di J. X. Mitrovica, C. C. Hay, E. Morrow, R. E. Kopp, M. Dumberry & S. Stanley
Reconciling past changes in Earth’s rotation with 20th century global sea-level rise: Resolving Munk’s enigma (da ora Mitrovica et al., 2015)
Nei giorni scorsi abbiamo avuto modo di parlare (qui e qui) di due diversi modelli di variazione del livello del mare. Si trattava di due modelli semiempirici che “riconciliavano” gli output del modello fisico a base del 5° rapporto IPCC con i risultati roboanti della precedente generazione di modelli semiempirici. In un’altra occasione ho commentato un altro articolo in cui si analizzava il legame tra transizioni geomagnetiche e livello del mare.
In Mitrovica et al., 2015 si analizza il modo di variare del livello del mare nel corso del 20° secolo tenendo presenti molti dei fattori che abbiamo avuto modo di vedere nei tre post precedenti. Molto interessante mi è parso il legame tra l’assestamento isostatico (legato al livello del mare) ed i moti relativi del nucleo esterno rispetto al mantello: in questa ottica acquista maggior valore l’ipotesi di un legame tra campo magnetico terrestre e livello del mare avanzata da De Santis, 2013.
Procediamo, però, con ordine. Partiamo dall’antefatto. Nel 2002 W. Munk pubblicò su PNAS questo articolo:
Twentieth century sea level: An enigma (da ora Munk, 2002)
Si tratta di un breve articolo in cui viene messa in evidenza una grossa discrepanza tra il rateo di incremento del livello dei mari previsto dai modelli e quello rilevato dai mareografi. Mitrovica et al., 2015 è incomprensibile senza aver prima studiato tale articolo (che ad onor del vero è molto più chiaro anche dal punto di vista logico-espositivo).
Come ormai sappiamo a memoria il livello del mare è determinato da due contributi fondamentali: il contributo sterico legato alla dilatazione termica degli oceani ed il contributo di massa dovuto allo scioglimento dei ghiacciai terrestri (ghiacciai montani e calotte glaciali antartica e groenlandese) ed alle variazioni dell’invasamento delle acque terrestri (superficiali e sotterranee).
Alla fine dell’ultima fase glaciale (intorno ai 20000 anni fa) il livello del mare era di circa 120 metri più basso di quello odierno. Con l’inizio dell’attuale interglaciale il livello del mare cominciò a salire e, in circa 8000 anni, raggiunse un livello di circa 25 metri inferiore a quello attuale. Nei successivi 4000 anni il livello del mare crebbe ancora, ma con un ritmo decisamente inferiore, fino a portarsi a pochi centimetri dal livello attuale. Nel 2000 avanti Cristo la deglaciazione era completa per cui il livello del mare negli ultimi 4000 anni è rimasto pressoché costante o, per essere più precisi, ha oscillato intorno al livello attuale. Alla fine della LIA nel 1850 circa il livello del mare ha cominciato a crescere ad un ritmo di circa 18 centimetri per secolo (tasso di crescita storico) fino al 1950 circa. Tale dato deriva dalle osservazioni mareografiche registrate tra gli inizi del 1800 e la metà del 20° secolo. A partire da questa data ha cominciato a farsi sentire l’effetto serra, per cui il livello del mare sembra che abbia accelerato la sua crescita.
Il modello elaborato dagli scienziati prevedeva che il livello del mare al 2000 doveva essere determinato dal tasso di crescita storico (18 cm a partire dal 1900) più il contributo dovuto al riscaldamento globale che fu stimato sulla base dei modelli e delle misure in circa 3 centimetri. Ciò significa che il livello del mare nel 2000, rispetto al 1900, era cresciuto di 21 cm (il contributo storico più il contributo dovuto al riscaldamento globale).
Andiamo a vedere adesso la “composizione” di questi 21 centimetri. Il tasso storico ha sia una componente sterica che una componente eustatica (contributo di massa). Nel rapporto del 2001 dell’IPCC il contributo eustatico globale fu fissato in 6 cm per secolo. La differenza
21-(3+6)=12 ,00 cm
rappresenta l’incremento del livello del mare al 2000 rispetto al 1900 di cui gli scienziati ignoravano la natura e che dal 2002 è conosciuto come “enigma di Munk”.
Posto che i 12 cm di residuo fossero stati di natura sterica (come pensavano quasi tutti), il contenuto di calore degli oceani avrebbe dovuto essere di un ordine di grandezza superiore a quello stimato da Levitus, per cui tale ipotesi doveva essere scartata.
Un’altra possibile spiegazione poteva essere cercata nel fatto che il residuo di 12 cm era stato determinato sulla base dei dati registrati da strumenti in buona parte concentrati nell’emisfero nord (quello che si è maggiormente riscaldato dopo il 1850). In tal caso il residuo di 12 cm sarebbe stato conseguenza di un accidente locale che non avrebbe inficiato le stime del contenuto di calore degli oceani effettuato da Levitus.
Un’ulteriore spiegazione poteva essere ricercata nel fatto che le stime del contenuto di calore degli oceani non tenevano conto del contenuto di calore negli oceani profondi o ne tenevano conto in modo relativo, ma in questo caso sarebbe stato necessario che il contributo all’innalzamento del livello del mare degli oceani profondi dovesse essere circa il doppio di quello della parte superficiale.
Una spiegazione alternativa era che il tasso di aumento del livello del mare fosse dovuto a fenomeni ciclici come, per esempio, El Nino. In questo caso il contributo storico all’aumento del livello del mare poteva essere stato determinato erroneamente a causa di misurazioni viziate da fenomeni pseudo-periodici per cui nel futuro poteva cambiare il suo segno.
Posto, invece, che il residuo fosse stato di natura eustatica, l’ablazione delle masse glaciali avrebbe dovuto essere enormemente superiore a quella stimata. Tale soluzione determinava, tra l’altro, delle grosse incongruenze a livello geodinamico.
Noi siamo abituati a credere che i moti celesti siano regolari ed immutabili nel tempo, quindi, facilmente prevedibili. In realtà gli elementi di disturbo dei parametri cinematici, geometrici e dinamici dei moti terrestri (geodinamici, per dirla in breve) sono molteplici e non prevedibili con le equazioni della meccanica celeste se non a breve termine. Con qualche approssimazione in più e con l’uso di equazioni goniometriche e trigonometriche, si riesce a prevedere un po’ più lontano nel tempo, ma a fronte di una diminuzione di precisione. Negli ultimi anni, grazie alla potenza di calcolo dei computer, le previsioni dei parametri orbitali e rotazionali della Terra sono calcolate numericamente ed estrapolate nel tempo, ma a breve distanza temporale esse perdono affidabilità (Astronomia, paleoclimatologia ed evoluzione umana – Elio Antonello, 2015).
Munk, 2002 calcola la variazione della velocità di rotazione terrestre sulla base di tre diversi tipi di dati osservativi. A partire dall’analisi di testi storici risalenti fino al 500 aC, si è potuto stimare il ritardo accumulato dalle eclissi fino al 1600 CE (Common Era): circa 16000 s corrispondenti a circa 4,5 ore. Detto in termini diversi, posto a base delle misurazioni la velocità di rotazione della Terra nel 1820 CE la durata del giorno terrestre dal -500 CE al 1990 CE è aumentata di circa 1,7 ms/secolo.
Ottenere una tale precisione sulla base delle testimonianze storiche può sembrare presuntuoso, ma esse sono supportate da alcune osservazioni moderne, come vedremo nel prosieguo.
Cerchiamo adesso di spiegare le ragioni del rallentamento della rotazione terrestre. L’interazione Terra-Luna determina il fenomeno delle maree. Dal punto di vista dinamico il sistema Terra-Luna può essere considerato un sistema isolato caratterizzato da momento angolare costante. Le maree e gli attriti connessi alle maree determinano, però, uno scambio di momento angolare tra Terra e Luna che determina una riduzione della velocità di rotazione della Terra. Sulla base di misurazioni della variazione della distanza Terra-Luna effettuate con strumentazione laser, si è potuto stimare il contributo mareale alla riduzione della velocità di rotazione della Terra: 2,3 ms/secolo.
Il rimbalzo glaciale conseguente allo scioglimento dei ghiacciai terrestri determina una diminuzione del momento d’inerzia della Terra (causato da una diminuzione dello schiacciamento polare) per cui la velocità di rotazione della Terra tende ad aumentare (come capita al pattinatore che ritira braccia e gambe durante il suo esercizio) e ciò comporta una riduzione della lunghezza del giorno di circa 0,6 ms/secolo. Tale valore è stato calcolato utilizzando, per la Terra, un modello elasto-plastico del rimbalzo post-glaciale che in Mitrovica et al., 2015 viene definito VM1.
Lo scioglimento dei ghiacci che ha riguardato anch’esso essenzialmente le alte latitudini, determina un flusso idrico dai poli all’equatore con conseguente aumento del momento d’inerzia terrestre, riduzione della velocità di rotazione del pianeta e contestuale aumento della durata del giorno terrestre. Questo aumento, sulla base delle stime del volume di ablazione delle calotte polari terrestri e dei ghiacciai continentali su cui si era verificato il consenso nel 2002, era di circa 1,2 ms/secolo.
Sommando con il loro segno tutti questi contributi, si ottiene una riduzione della durata del giorno terrestre di 2,9 ms/secolo che collima poco con il dato desunto dallo storico delle eclissi.
Le variazioni del momento d’inerzia della Terra sono state misurate indirettamente a partire dalla variazione della linea dei nodi dei satelliti in orbita bassa. Tale variazione è legata alla variazione del momento d’inerzia terrestre. Queste misurazioni, poiché limitate ad un breve arco di tempo, non sono, però, in grado di quantificare in maniera corretta un parametro millenario. Esse offrono, comunque, un utile elemento di controllo che può essere utilizzato per limitare il contributo di massa alla variazione del livello del mare.
L’entità della diminuzione del giorno terrestre, oltre che dai dati storici delle eclissi, può essere desunta anche da un’altra osservazione indipendente: l’intensità e la direzione del vettore che caratterizza il “movimento polare”. Fin dal 1800 si sa che i poli subiscono dei movimenti, nel senso che “vagano” in modo piuttosto regolare. Le variazioni del momento d’inerzia terrestre connesse al GIA ed alle variazioni eustatiche (massa degli oceani) sono in grado di contribuire al movimento dei poli. La fortunata circostanza che i due centri di fusione delle calotte glaciali terrestri (Groenlandia a nord ed Antartide a sud) sono disposti in posizione non simmetrica (l’Antartide quasi in corrispondenza con l’asse polare, la Groenlandia in posizione più decentrata) consente di orientare e quantificare il vettore del movimento polare. Complessi calcoli geodinamici hanno consentito di accertare che il valore e la posizione di tale vettore è perfettamente compatibile con un rimbalzo isostatico post glaciale e con un contributo di massa all’incremento del livello del mare, quasi coincidenti con quelli necessari per giustificare la diminuzione della durata del giorno calcolata con il modello delle eclissi. Nella figura che segue (tratta da Mitrovica et al, 2015, fig. 1) un riassunto di quanto detto fino ad ora.
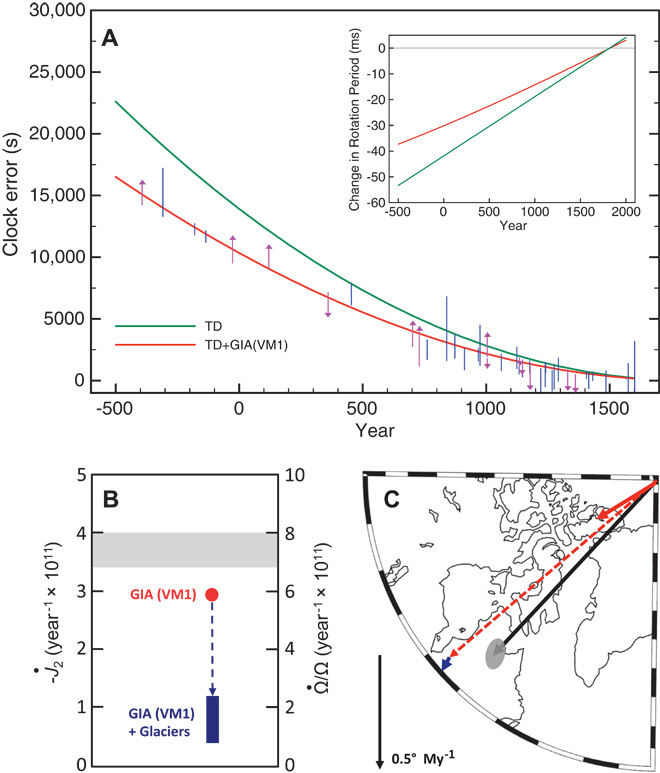
Detto fuori dai denti nel 2002 ci si trovava in una situazione piuttosto imbarazzante per gli scienziati: se il contenuto di calore degli oceani era quello calcolato da Levitus ed il rimbalzo isostatico post glaciale quello stimato, non esisteva lo spazio per giustificare il contributo di massa all’aumento del livello del mare individuato in IPCC 2001 in quanto avrebbe determinato una incongruenza con i dati storici ed osservativi legati alla rotazione della Terra e, in particolare, al rallentamento della sua velocità di rotazione. Ci si trovava di fronte ad una situazione classica in climatologia: i modelli generano risultati diversi da quelli che scaturiscono dalle osservazioni. Munk conclude la sua fatica con un’amara considerazione che non è nuova per i lettori di CM: vogliamo prevedere il livello del mare a fine 21° secolo, ma non sappiamo come esso è variato nel 20° secolo!
Questo è, in buona sostanza, l’enigma di Munk.
Solo a titolo di curiosità vorrei far notare che nella figura 1 la linea rossa che rappresenta il contributo mareale al rallentamento della rotazione terrestre è posta al di sopra di quella rappresentativa del contributo mareale e GIA sommati insieme. La contraddizione è solo apparente, in quanto essi sono di segno opposto.
Lo stesso Munk elaborò una serie di condizioni cui doveva soddisfare la soluzione del suo enigma e che, in estrema sintesi, possono essere così enunciate:
- una riduzione sostanziale delle stime tradizionali del tasso di aumento del livello del mare (compresa quella di Munk) che nel 2002 era di 1,5-2 mm/anno;
- un sostanziale aumento delle stime di accumulo di calore nell’oceano durante il 20° secolo;
- un cambiamento sostanziale nella interpretazione del modello astronomico.
A distanza di oltre 13 anni dalla pubblicazione di Munk, 2002, Mitrovica et al., 2015 sembra che sia riuscito a risolvere l’enigma di Munk. Mitrovica et al., 2015 parte dal fatto che recenti stime del tasso di variazione del livello del mare ne hanno ridotto il valore da circa 1,5-2 mm/anno a circa 1,2 mm/anno. Ciò significa che non è necessario prevedere un aumento del contenuto di calore degli oceani rispetto a quello calcolato da Levitus, né un valore irrealistico del tasso di fusione delle calotte glaciali, per cui si possono considerare soddisfatte due delle tre condizioni a cui deve sottostare la soluzione dell’enigma di Munk.
Detto in altri termini, nel 2002 si sopravvalutava di molto il tasso di aumento del livello del mare. Le osservazioni hanno consentito di ridurne la stima e, a questo punto, i conti cominciano a tornare. In tali ipotesi il contributo di massa all’aumento del livello del mare derivante dallo scioglimento dei ghiacciai continentali può essere posto pari a 0,7 mm/anno, quello sterico a 0,4 mm/anno e quello dovuto all’invasamento delle acque terrestri a -0,11 mm/anno. In altri termini tra il 1900 ed il 1990 appare congruo un tasso di variazione del livello del mare di circa 1 mm/anno. A questo punto l’unica condizione da rispettare per conciliare osservazioni e previsioni è il modo di interpretare il modello astronomico.
Mitrovica et al., 2015 ha individuato un modello del comportamento della Terra sostanzialmente diverso da quello utilizzato nel 2002. Il pianeta viene schematizzato non come un unicum elasto-plastico che si comporta come un corpo viscoso omogeneo, ma come una serie di strati che ruotano a velocità differenti a causa di viscosità differenti. Ciò determina, ovviamente, scambio di momento angolare tra strati diversi e diverso modello del rimbalzo isostatico post-glaciale. Nella fattispecie si sono ipotizzati dei profili di viscosità per i diversi strati del pianeta. In particolare si sono indagati il nucleo esterno del pianeta e la base del mantello. Il modello consente, a questo punto, di attribuire la variazione di momento angolare del pianeta oltre che a cause esterne (aumento del livello del mare e rimbalzo isostatico post-glaciale) anche a cause interne allo stesso: strati a differente viscosità che, ruotando, si scambiano momento angolare.
Questo schema appare coerente anche con i risultati di rilievi paleomagnetici che sembrano corroborare una differente viscosità tra le parti esterne del nucleo e quelle interne del mantello.
Il nuovo modello terrestre comporta un diverso valore dell’assestamento isostatico post glaciale e un diverso valore del contributo eustatico all’aumento del livello del mare. La somma di questi due contributi è tale da conciliare le osservazioni con la teoria. Nella figura che segue, tratta dalla figura 3 di Mitrovica et al., 2015, un sunto di quanto esposto.
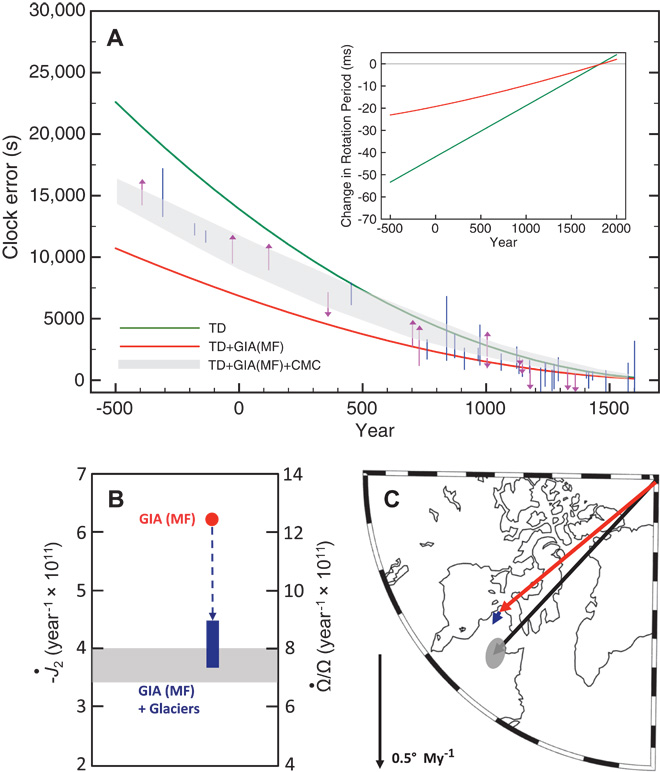
Mitrovica et al., 2015 ha in buona sostanza ridotto di una significativa quantità il tasso di aumento del livello del mare tra il 1900 ed il 1990 (da 1,5÷2 mm/anno a 1÷1,2 mm/anno) ed ha fornito un’interpretazione del tutto originale del modello astronomico riducendo notevolmente la stima del rimbalzo isostatico post glaciale, introducendo un nuovo modo di dissipazione del momento angolare del pianeta. In tal modo si è creato spazio per un ulteriore piccolo aumento del contributo di massa al livello medio del mare (circa 0,2 mm/anno) che consente di passare da 1 a 1,2 mm per anno.
L’aspetto più importante di Mitrovica et al., 2015 è però l’individuazione di un modello di variazione del livello del mare che può essere estrapolato con maggiore fiducia fino alla fine del 21° secolo in quanto riesce a spiegare la variazione del livello del mare del passato.
Sorge ora spontanea una domanda: tale modello riuscirà a fornirci previsioni affidabili?
Rispondere è secondo me piuttosto difficile per diversi ordini di motivi. In primo luogo tutto si basa sul fatto che il contenuto di calore degli oceani stimato da Levitus sia corretto, ma stando a quanto si legge in giro la cosa non è del tutto certa in quanto crescono le stime del contenuto di calore nella fascia di profondità maggiore di 2000 m. In secondo luogo i modelli accoppiati atmosfera-oceani non riescono a simulare in modo soddisfacente la temperatura dei prossimi decenni ed il sistema climatico terrestre per cui appare piuttosto difficile prevedere le condizioni climatiche di qui ad oltre mezzo secolo. In terzo luogo non siamo sicuri che con l’aumento del periodo delle osservazioni satellitari tutta l’impalcatura teorica che sottosta a Mitrovica et al., 2015 sarà in grado di reggere alle osservazioni.
Detto in altri termini la scienza non è ancora chiara: almeno per quel che riguarda il livello del mare. Questo non ci deve impressionare, però, perché è nella natura stessa della scienza anche se molti se ne dimenticano.
Caro Gianluca, ho letto il punto dello studio da te citato e sono restato molto perplesso. La dilatazione termica è volumica: sempre ed in ogni caso. La legge di dilatazione dei corpi è lineare e dipende dal volume iniziale: maggiore è il volume iniziale, maggiore sarà la dilatazione termica. Ciò in termini modellistici, ma i modelli non sono molto diversi dalla realtà, viste le applicazioni tecniche che si basano sul fenomeno fisico della dilatazione termica dei corpi (termometri, termocoppie e via cantando). Nel caso dei binari noi consideriamo la dilatazione termica lineare perché la variazione di lunghezza che misuriamo nella direzione della lunghezza è enormemente maggiore di quella nelle due direzioni ad essa ortogonali.
L’autore da te citato ipotizza che la variazione del livello del mare per effetto dell’aumento di temperatura avvenga secondo la verticale: come se l’acqua fosse costituita da tante piccole barrette verticali, indipendenti l’una dall’altra, che si allungano secondo la dimensione prevalente. In base a questo modello il suo ragionamento non fa una grinza: l’incremento del livello del mare è maggiore dove è maggiore la profondità. Peccato che tale modello sia, a mio giudizio, poco aderente alla realtà fisica del problema.
Immaginiamo, infatti, di fare un semplice esperimento. Versiamo dell’acqua in una pentola di forma conica e riscaldiamola: sulla base del ragionamento dell’autore dell’articolo da te citato, la superficie dell’acqua nella pentola dovrebbe avere la forma di un cono con la punta verso l’alto. Francamente mi sembra un assurdo fisico in quanto la superficie dell’acqua non sarebbe più equipotenziale e ciò contraddice tutte le leggi fisiche che io conosco.
Per quel che mi riguarda credo che l’autore dell’articolo che tu hai citato abbia preso un granchio grande come il … mare! 🙂
p.s.: io non sono un esperto di livello del mare in quanto non mi occupo per professione di studiare il livello del mare, diciamo che sono un appassionato e che studio da oltre un lustro queste problematiche dedicando ad esse molte ore notturne e molte ore del mio tempo libero (troppe, secondo mia moglie) 🙂 .
Ciao, Donato.
Caro Donato,
ti scrivo in quanto “esperto i livelli oceanici”.
Seguendo alcune ricerche mi sono imbattuto nel seguente papero
https://www.google.it/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0ahUKEwjErbmrlfrLAhWBqSwKHcHmA9UQFggiMAA&url=http%3A%2F%2Fijera.com%2Fpapers%2FVol5_issue1%2FPart%2520-%25205%2FU50105124129.pdf&usg=AFQjCNFvP0-7ZigjW8ELxkNZWlXq9yCBbQ
e sono rimasto colpito da quanto sostenuto nel paragrafo 2, in particolare quando si sostiene che l’espansione termica causa un aumento nullo in prossimita’ delle coste. Ho provato a seguire le referenze (tra l’altro tutte allo stesso autore) e ti confesso che quanto sostenuto cozza contro le mie convinzioni. Cosa ne pensi?
Grazie,
Gianluca
Scrive A de Orleans-Borbone
“….come determino, per una stazione di misura del livello del mare, la stabilità nel tempo del suo riferimento? E se affondasse o emergesse?”
.
Domanda assolutamente in tema.. L’assestamento isostatico che rappresenta un bias positivo o negativo per la stazione mareografica viene determinato, per ogni mareografo, sulla base di un modello globale dell’assestamento isostatico post-glaciale, ovvero sulla base di un modello della viscosità interna del pianeta e ciò rappresenta la più grossa fonte di incertezza di tutti i modelli di ricostruzione del livello del mare, anche di quelli basati su rilievi satellitari (GRACE, per esempio).
Il problema è veramente affascinante!
Ciao, Donato.
Affascinante, grazie!
.
Ogni volta che leggo quanto poco si sappia su un tema che a prima vista sembrerebbe chiaro, penso quanta curiosità scientifica resti ancora da soddisfare…
.
E su tema di questo saggio, mi resta — sicuramente per ignoranza — una curiosità insoddisfatta: come determino, per una stazione di misura del livello del mare, la stabilità nel tempo del suo riferimento? E se affondasse o emergesse?
.
Ad esempio: sappiamo con ragionevole certezza quanto sia il volume totale delle terre emerse e quanto questo volume varii nel tempo e per quali motivi? Questo volume è (o almeno mi sembrerebbe) collegato con la stabilità “collettiva” del riferimento di tutte le stazioni di misura — e se vi fosse un “bias” generale?
.
Solo come esempio, magari qui del tutto inapplicabile: ho personalmente molta esperienza pratica con un dato poco “vissuto” anche tra i geologi, quello della estrema non-linearità della viscosità del magma terrestre, prevalentemente siliceo (perdonatemi l’improprietà geologica dei termini!), al variare della sua temperatura. Una variazione di pochi gradi attorno ai 1200 gradi C, può determinare il suo passaggio da fluido a praticamente solido.
.
Quanto sappiamo sulla stabilità a lungo termine della temperatura dello strato del magma sul quale “galleggiano” le terre emerse e sul corrispondente “tasso di riassorbimento” delle medesime? Sulle scale dei tempi geologici queste terre emerse hanno la durata metaforica della schiuma di un cappuccino… se il volume totale emerso variasse di conseguenza, che significato posso attribuire al concetto di “livello medio del mare”?
.
Fine della mia “congettura ignorante” — ma l’idea è solo quella di sottolineare la complessità di questo tema affascinante!
allora, vediamo:
attualmente si calcola un valore per la superficie delle terre emerse pari a circa 149 milioni di kmq, e la quota media, ricavata dalla distribuzione sulla curva ipsografica, di circa 820-840 m slm
vedi fig. http://images.treccani.it/enc/media/share/images/orig//system/galleries/NPT/VOL_X/IMMAGINI/terra_05.jpg
quindi il calcolo del volume totale è abbastanza agevole, anche se in termini di evoluzione della superficie terrestre (parlo nell’ordine dei tempi geologici, è più importante la superficie che il volume);
fondamentalmente ciò che è alla base di grosse variazioni dell’estensione (e del volume) delle terre emerse, sono i cicli orogenici, in particolar modo nelle situazioni in cui la collisione tra placche coinvolge due (o più) placche di crosta continentale;
mi spiego meglio: in questi casi, dato che non ci sono differenze apprezzabili di densità tra i due blocchi che si “scontrano” (si assume di base una densità media assimilabile ad una litosfera di composizione granitica), la collisione determina un ispessimento crostale notevole, la nascita di catene montuose rilevanti (è il caso di Alpi, Himalaya, Appenini, e in un passato più lontano, Urali), e una scarsa, per i motivi di densità suddetti, subduzione di una placca sotto l’altra;
quindi, di fatto, come risultato finale, in questi casi un aumento di terre emerse a scapito di bacini oceanici;
ciò non toglie che l’equilibrio tra terre emerse e non, è uno dei tanti cosiddetti “equilibri dinamici”, cioè variabile in continuazione, anche perché ogni terra emersa, in funzione della caratterizzazione climatica della zona in cui si trova, e della quota media che raggiunge, è quotidianamente sottoposta ai processi di erosione e degradazione meteorica, che erodono “terra” e, tramite tutti i meccanismi di trasporto subaereo e idrologico, alla fine riportano in mare ciò che viene eroso (tutto, o quasi).
per quel che riguarda i magmi – si, sono tutti a base silicatica, non è un errore dirlo 🙂 – in % di SiO2 che variano dal 48-50% (magmi basici) al 65-67% (magmi acidi), diciamo che la variabilità del campo di T° in cui si osservano varia dai 1200 ° ai 650° (un po’ più di qualche decina di gradi quindi) , ovviamente oltre la % di SiO2 molto dipende dalla pressione a cui sono sottoposti, nonché dalla pressione parziale del contenuto in H2O;
sulla stabilità dello “strato di magma”, in altre parole di quella parte di mantello a cui si attribuisce un comportamento meccanico di fluido molto viscoso (astenosfera), beh, il discorso è complicato, però si dà per scontato (per ora) che la maggior parte della fonte di calore che mantiene attivo il motore termodinamico interno del pianeta, derivi dal decadimento radioattivo degli elementi, in particolare per emissione di particelle alfa dagli isotopi di U238, Th232, e K40; se così è, è scontato che prima o poi si esaurirà…. quando? bella domanda… credo che comunque noi e le successive 1000 generazioni, possano stare tranquilli 🙂
lascio la palla a Donato, per ulteriori considerazioni a più ampio raggio… 🙂
Caro Max, ti ringrazio per le tue precisazioni.
Per risponderti inverto l’ordine con cui tu le hai formulate.
In merito alla nota 2 hai perfettamente ragione: mea culpa!
In merito alla nota 3 … anche 🙂 . Nel post ho parlato di profili omettendo di precisare che si trattava di profili sismici (a mia parziale scusante non è precisato neanche nell’articolo di Mitrovica, ma non ha importanza). Allo stesso tempo mi rendo conto di non aver specificato che gli stessi erano noti da tempo e che Mitrovica et al., 2015 li ha utilizzati per elaborare i suoi calcoli: diciamo che è stato l’utilizzatore finale del prodotto confezionato da altri. 🙂
.
La prima considerazione che hai fatto merita, invece, qualche commento ulteriore. Forse più di uno. 🙂
Il tuo ragionamento non fa una grinza e lo condivido in pieno: da un punto di vista geometrico hai completamente ragione e ciò, con un poco di pazienza, è dimostrabile.
.
Approssimando il geoide ad una sfera omogenea il suo momento di inerzia, riferito all’asse di rotazione, è dato dalla formula
I=2/5MR*2
La Terra non è, però, omogenea e tanto meno lo è quando è parzialmente coperta da una coltre glaciale molto spessa.
per cui l’integrale che ci dà la formula, deve essere sostituito da una sommatoria con le conseguenti complicazioni del caso. Se ci mettiamo in questa seconda ipotesi, vediamo che il momento d’inerzia della Terra è la somma degli N momenti d’inerzia dei dischi in cui immaginiamo di aver diviso la Terra stessa. In questo caso il momento d’inerzia del singolo disco è legato al quadrato del suo raggio ed alla massa del singolo disco per cui il contributo delle zone polari al momento d’inerzia totale è minore di un disco di uguale massa posto in area equatoriale.
.
Durante le glaciazioni le masse d’acqua tendono a spostarsi dall’equatore ai poli. Durante questa “migrazione” la massa d’acqua equatoriale si avvicina all’asse di rotazione per cui, a parità di massa, viene moltiplicata per un raggio minore e, quindi, determina un momento d’inerzia più basso. Il risultato netto, a rigore di logica, dovrebbe essere un momento d’inerzia più piccolo rispetto a quello precedente e successivo alla glaciazione.
.
Con l’avvento dell’interglaciale il processo si inverte e succede quello che hai detto tu.
.
Munk citando Peltier, però, dice cose diverse che io, forse, ho eccessivamente semplificato: egli sostiene che dopo il disgelo si sia verificato un flusso sub-crostale di materia diretto verso i poli che ha determinato il rimbalzo post-glaciale e la diminuzione del momento d’inerzia planetario.
.
“The residual spin-up (negative τ̇) is attributed to the decrease in the Earth’s moment of inertia associated with the postglacial flow toward the polar regions previously glaciated. Peltier ( 7 ) finds that the same geodynamic model that produced sensible corrections at individual tide gauges (and agrees with other geodetic measurements) is consistent with τ̇ rebound = −0.6 ms/cy.”
.
Come puoi vedere il rimbalzo viene attribuito a flussi di materia che da aree lontane dai poli si dirigono verso i poli modificando il geoide ovvero lo schiacciamento polare e riducendo il momento d’inerzia. La cosa è stata da me interpretata come “una riduzione dello schiacciamento polare”.
Ciao, Donato.
rimango molto dubbioso….
certo, in Scandinavia e nel nordest del Canada, il sollevamento isostatico in risposta alla deglaciazione è stato dell’ordine dei 80-120 metri, ma in corrispondenza dell’oceano artico, e del polo nord geografico, dove passa “più o meno” con tutte le sue oscillazioni, l’asse di rotazione terrestre, glaciazione o no, non c’è né c’è mai stato un peso supplementare che possa aver “deformato” l’astenosfera in maniera differenziale tra periodo glaciale e interglaciale; sempre di ghiaccio su acqua parliamo…
discorso interessante comunque….
grazie ancora 🙂
… t’ho fatto lavorare, eh? 🙂
allora: quello che non mi convince è:
“Il rimbalzo glaciale conseguente allo scioglimento dei ghiacciai terrestri determina una diminuzione del momento d’inerzia della Terra (causato da una diminuzione dello schiacciamento polare)”
partiamo da un presupposto: durante l’ultima glaciazione le coltri glaciali erano enormemente più estese di oggi nell’emisfero settentrionale, occupando però molte terre emerse a latitudini anche prossime ai 50-60°, quindi poco influenti per uno schiacciamento centrato al polo nord, mentre la zona dove l’effetto schiacciamento sarebbe dovuto essere al massimo, è l’artico, cioè ghiaccio su acqua, dove pertanto l’effetto schiacciamento qui non ci può essere;
di contro, in Antartide, il continente è interamente circondato da oceano, e seppur sicuramente fosse più estesa di oggi oltre le coste e il margine della piattaforma continentale, non ci sono ad oggi evidenze che ci fosse continuità tra la calotta antartica e coltri glaciali in Patagonia, o nel sud della Nuova Zelanda; e per quel che mi risulta, non ci sono dati per stabilire di quanto fosse più spessa rispetto ad oggi (può darsi che mi sbaglio), mentre addirittura sembra plausibile che la calotta antartica orientale fosse meno spessa di oggi (http://www.sciencedirect.com/science/article/pii/S0277379101000828)
se le mie considerazioni sono fondate (e sottolineo SE), perché chiamare in causa la ipotetica “diminuzione dello schiacciamento” del geoide terrestre ai poli, quando così a intuito direi che il semplice scioglimento e conseguente sparizione di calotte glaciali da Nord America, e Scandinavia, abbia prodotto una “diminuzione di massa complessiva” tale da provocare a sua volta “una diminuzione del momento d’inerzia della Terra” e quindi un (minimo) aumento della velocità di rotazione?
note a margine:
1: le differenze di viscosità , come anche di densità, e di risposta alle sollecitazioni meccaniche, dei vari “strati” di mantello e nucleo terrestre, sono teorizzate e indirettamente dimostrate già da tempo, ben prima dell’articolo di Mitrovica; derivano soprattutto dall’applicazione della cosiddetta tomografia sismica, osservando le rifrazioni, riflessioni, e “smorzamenti” che subiscono i vari tipi di onde sismiche, durante la loro propagazione e percorrenza all’interno del pianeta;
2: il termine “geodinamica” che hai usato, seppur comprensibilmente, associandolo ai moti celesti e ai fattori di disturbo, in realtà ha accademicamente tutt’altro significato, si riferisce in particolare ad una branca specifica della geologia che correla e studia l’evoluzione tettonica e geologica nel suo insieme, focalizzandosi sulle cause endogene ed esogene che condizionano l’evoluzione della litosfera, quindi le sue deformazioni, in funzione dell’assetto geologico-strutturale e delle relazioni mantello-crosta;
per questo sono rimasto un po’ spaesato leggendoti, perché continuavo inconsciamente ad associargli il significato che invece mi era familiare 🙂
ti ringrazio ancora per aver dedicato tempo a elaborare questo post;