Rivisitazione delle serie storiche degli indici solari

Qualche tempo fa G. Guidi ha pubblicato un post (qui su CM) in cui, tra l’altro, si dava notizia dello  studio liberamente accessibile pubblicato su Space Science Reviews, Volume 186, Issue 1-4, pp. 35-103:

Revisiting the Sunspot Number. A 400-Year Perspective on the Solar Cycle di Clette, F., Svalgaard, L., Vaquero, J.M., Cliver, E. W.

Si tratta di un lavoro imponente (oltre 60 pagine ed altrettante tabelle e grafici) che presenta molti spunti interessanti sia dal punto di vista metodologico che storico.

Lo studio, da ora Clett et al., 2014, si occupa della serie storica del Numero di Wolf o Solar Number (SN) o Solar Spot Number (SSN) e della sua divergenza con un’altra serie storica definita del numero di gruppi di macchie solari o Group Solarspot Number (GN o GSN). In entrambi i casi ci troviamo di fronte ad indici che consentono di quantificare in qualche modo l’attività del Sole. Nel caso del numero di Wolf dato il numero di macchie solari (Ns) e il numero di gruppi di macchie solari (Ng) e un opportuno coefficiente k che tiene conto delle caratteristiche soggettive dell’osservatore, mediante l’equazione

R = k(10×Ng+Ns)

dovuta a R. Wolf si ottiene un indicatore in grado di quantificare le fasi del ciclo solare undecennale.

Il valore così calcolato non è una misura fisica in quanto non è in grado di quantificare alcuna delle grandezze fisiche che caratterizzano l’attività solare, ma rappresenta un numero su una scala arbitraria e, quindi, “relativo” (questo è il significato di R).  L’indice in questione fu elaborato da R. Wolf e fu oggetto di discussione nell’ambito della comunità scientifica a seguito della pubblicazioni di due lavori (Wolf, 1851 e Wolf, 1856). Il numero R di cui alla precedente equazione veniva calcolato da una serie di osservatori che erano in corrispondenza con Wolf per cui, appena dopo la pubblicazione dei due lavori, fu necessario risolvere due problemi:

• le osservazioni dovevano essere normalizzate, cioè gli osservatori dovevano utilizzare lo stesso strumento di misura (telescopio) e lo stesso metodo di conteggio delle macchie. In mancanza doveva essere applicato un coefficiente correttivo in grado di ridurre tutte le osservazioni ad un unico “denominatore”;
• era necessario realizzare una serie di dati la più lunga possibile integrando anche i risultati delle osservazioni fatte nei decenni e nei secoli precedenti.

In termini moderni possiamo dire che era necessario omogeneizzare le misure su cui si basava l’indice SN. All’epoca esistevano diverse serie di osservazioni che documentavano le macchie sul disco del Sole e che risalivano agli anni in cui si iniziò ad utilizzare il telescopio.

In altri termini la serie storica dei dati SN non è affatto il risultato di un unico modello di misurazione, ma è il frutto della composizione di diverse serie di dati più o meno lunghe e caratterizzate dalla soggettività dell’osservatore e dai criteri che egli assumeva a base del suo lavoro. Wolf iniziò ad osservare e registrare sistematicamente il numero di macchie solari a partire dal 1849 dopo aver preso visione della lunghissima serie di osservazioni effettuate da Samuel Heinrich Schwabe che, grazie ad esse, era riuscito ad individuare il ciclo circa decadale che porta il suo nome. Schwabe aveva iniziato ad osservare il Sole nel 1825 e le sue osservazioni si interruppero nel 1868, pochi anni prima della sua morte, quindi coprivano un intervallo di oltre quarant’anni e per circa venti anni si sovrapponevano a quelle di Wolf. La sovrapposizione delle due serie (l’oggetto dell’osservazione era lo stesso) consentì di estendere il numero SN fino al 1825.

Nel 1857 Wolf estese ulteriormente la ricostruzione storica utilizzando un’altra serie di osservazioni molto lunga che copriva il periodo compreso tra il 1749 ed il 1796 e dovuta a Johann Caspar Staudach che riprodusse le sue osservazioni in disegni conservati attualmente presso la biblioteca del Leibniz Institute di Astrofisica di Potsdam in Germania. A proposito di questa serie bisogna precisare che le osservazioni coprono 1016 giorni con una media di circa 21 osservazioni all’anno e che i giorni di osservazioni, nel corso dell’anno solare, sono sporadici e sparsi in modo casuale nel tempo. Si può dire, pertanto, che l’attuale serie SN è il composito di tre serie principali di osservazioni: la serie di Staudach, la serie di Schwabe e la lunghissima serie di Zurigo dovuta a Wolf ed agli astronomi che gli succedettero fino al 1980. Dal 1980 il testimone passò a Bruxelles e, in particolare, al locale Osservatorio astronomico.

L’intervallo tra il 1749 ed il 1825 fu colmato da Wolf (Wolf, 1874) attingendo ad altre serie di osservazioni piuttosto sporadiche e discontinue dovute principalmente a Flaugergues. Ottenuta la base di dati grezzi si poneva il problema di omogeneizzare i dati stessi per renderli confrontabili in quanto i periodi di sovrapposizione dimostravano che i conteggi effettuati con le varie metodiche risultavano poco congruenti.

Confrontando i disegni e le note di Schwabe, Wolf si rese conto che applicando ad essi la sua metodologia di calcolo dell’indice SN, per rendere i valori ottenuti confrontabili con quelli delle sue osservazioni, bisognava incrementarli del 25%. Wolf, pertanto, applicò un coefficiente correttivo di 1,25 a tutta la serie di Schwabe, anche nella parte in cui non si sovrapponeva alle sue osservazioni. In questo commise un errore di cui si rese conto il suo successore Wolfer che ridusse, sulla scorta di altre osservazioni che nel frattempo erano state rinvenute, i valori relativi al ciclo 5 (primo decennio del 1800) mediante l’applicazione di un coefficiente correttivo pari a 0,58. Per quel che riguarda la serie di Staudach,  Wolf applicò il suo algoritmo attribuendo a k il valore 2: ciò sulla scorta del fatto che i dati di Staudach erano sistematicamente più bassi di quelli di Schwabe probabilmente a causa di un telescopio meno sofisticato di quello di Schwabe (il tutto si basava sulla convinzione che i cicli del periodo di Staudach non dovessero avere ampiezza inferiore a quella di Schwabe).

Questo modo di procedere presta il fianco a diverse critiche a causa dell’attribuzione di valori piuttosto estemporanei ai vari coefficienti correttivi. In realtà Wolf si servì, per i cicli passati, di dati di prossimità di controllo. Nel 1722 G. Graham scoprì che gli aghi magnetici risentono delle perturbazioni indotte nella ionosfera dall’attività solare. Le osservazioni geomagnetiche effettuate a partire dal 1822 consentirono a Wolf di avere a disposizione un insieme di dati di prossimità attraverso i quali stimare l’ampiezza dei cicli solari che lui man mano riusciva a ricostruire sulla base dei dati osservativi. La scarsità di dati anteriori al 1749 non consentì a Wolf di ricostruire la serie storica mensile SN nel periodo antecedente il 1849: per questi anni si hanno a disposizione solo dati molto frammentari che al massimo riescono a generare serie di SN annuali.

Un breve cenno merita il modo in cui è stata costruita la lunga serie di dati successivi al 1849 e nota come “serie di Zurigo” dal nome della città in cui operò in modo continuativo Wolf e, in seguito, i suoi successori. Nel corso del 19° secolo la rete di osservatori che si occupò di osservazioni solari aumentò sensibilmente. Tutti gli osservatori si servivano di telescopi diversi per cui quando inviavano a Zurigo gli esiti delle loro osservazioni, tali esiti dovevano essere confrontati ed omogeneizzati. Zurigo rappresentava lo standard delle osservazioni e sui risultati ottenuti nella città elvetica venivano calibrati quelli delle stazioni periferiche: confrontando i risultati degli osservatori corrispondenti con quelli di Zurigo, si riusciva ad attribuire il coefficiente k agli osservatori corrispondenti posto k=1 per Zurigo.

Poiché non sempre i giorni di osservazione tra l’osservatorio di Zurigo e quelli degli osservatori corrispondenti coincidevano (a causa del maltempo, per esempio) i coefficienti k venivano determinati come media annuale dei dati di ogni singolo osservatore rispetto a Zurigo. Il valore SN veniva calcolato, infine, come media di tutti i valori provenienti dagli osservatori esterni. Il metodo di calcolo sommariamente descritto attribuisce un peso determinante alle osservazioni di Zurigo e quelle degli osservatori corrispondenti servono solo a colmare le lacune di Zurigo per cui si può dire che l’indice SN della serie di Zurigo è essenzialmente il dato di Zurigo.

La metodologia illustrata è rimasta invariata, salvo modifiche nel modo di ponderare le macchie solari, fino ai nostri giorni ed analisi statistiche dei risultati moderni consentono di affermare che il dato moderno si discosta di meno del 5% rispetto ai valori che sarebbero stati calcolati da Wolf in persona.

Wolf allo scopo di rendere la serie di dati odierna coerente con quella del passato, tenuto conto che gli osservatori che lo avevano preceduto avevano a disposizioni strumenti molto più rudimentali di quelli da lui utilizzati, individuò una serie di vincoli piuttosto rigidi cui dovevano attenersi gli osservatori:

• non bisognava conteggiare le macchie senza penombra e di breve durata (pori);
• più ombre all’interno di una stessa penombra dovevano essere contabilizzate come singole macchie solari.

Si tratta di criteri stringenti, ma anche piuttosto esposti alla soggettività dell’osservatore.

Leggendo Clette et al., 2014, mi sono reso conto che uno dei motivi per cui si utilizzò questo criterio deve essere ricercato anche nell’eccesso di protagonismo di Wolf. Egli viaggiava molto e, durante gli spostamenti, per osservare il Sole utilizzava un piccolo telescopio palmare che non consentiva la stessa risoluzione del telescopio rifrattore da 80 mm di Zurigo. Detto in altri termini ho avuto l’impressione che Wolf volesse avere sempre l’ultima parola circa il valore dell’indice SN (non per niente il valore del suo coefficiente personale era 1 per definizione). Questo fatto ha determinato la perdita di informazioni importanti per cui Wolfer, accanto al conteggio ufficiale, iniziò ad effettuare un conteggio parallelo che non teneva conto dei vincoli imposti da Wolf.

Sulla base dei confronti tra i risultati dei conteggi ufficiali e dei conteggi effettuati da Wolfer, nei sedici anni in cui le due serie si sovrappongono, si è potuto vedere che i conteggi di Wolfer per poter essere omogeneizzati a quelli ufficiali, dovevano essere moltiplicati per un coefficiente correttivo di 0,6 (che nulla ha a che fare con il coefficiente k dell’equazione di Wolf).

Fino al 1945 il conteggio di Wolfer fu utilizzato in modo piuttosto conforme alle indicazioni originarie per cui i dati raccolti possono essere considerati omogenei. Dopo il 1945 si è avuta, però, un’ulteriore modifica del modo di conteggiare il numero di macchie solari: fu introdotto un coefficiente di ponderazione che teneva conto delle dimensioni delle singole macchie solari. Tale metodo di calcolo è quello ancora oggi applicato alla Specola Ticinese di Locarno che ha sostituito, a partire dal 1981, l’osservatorio di Zurigo.

Nel 1980, con la chiusura dell’osservatorio di Zurigo, la custodia ed aggiornamento della serie storica è passata, come già accennato, all’Osservatorio Reale del Belgio a Bruxelles in cui si è insediato il Sunspot Index Data Center (SIDC) che, allo scopo di uniformare le rilevazioni del numero di macchie solari a quelle di Zurigo, ha individuato un nuovo modo di procedere per l’omogeneizzazione dei dati. Il nuovo SN è calcolato come media normalizzata di tutte le stazioni contribuenti e previo scarto dei valori che si discostano dalla media di rete (il controllo viene effettuato in modo statistico sul coefficiente k dell’equazione di Wolf). Questa metodologia molto più complessa di quella di Zurigo, porta, però ad un valore di SN di poco differente da quello calcolato originariamente da Wolf. La nuova metodologia risulta innovativa anche per il fatto che non esiste più una stazione di riferimento che in passato era quella di Zurigo: la stazione guida può cambiare giorno per giorno in quanto è quella che più si avvicina alla media di rete. In base a questa tecnica di conteggio può capitare di rigettare il valore di Locarno mentre con il vecchio metodo ciò non era possibile. Il cambio di metodo ha consentito un passaggio indolore dal periodo di Zurigo a quello di Bruxelles, ma ha determinato problemi in epoca successiva. Ad ogni buon conto la nuova metodologia di rilievo e calcolo del SN oggi consente di coprire, mediamente, circa 175 giorni all’anno di osservazioni per le singole stazioni e garantisce la copertura osservativa di ogni giorno dell’anno: il rilievo dell’indice SN si può considerare giornaliero.

Come si può vedere da questa rapida carrellata la serie storica dell’indice SN è frutto della composizione di molte ed eterogenee serie di dati e molti degli aggiustamenti effettuati nel corso dei secoli la rendono affetta da bias legati alla soggettività dei vari osservatori (vedi i coefficienti di correzione che sono stati via via introdotti).

Essa inoltre non copre uno dei periodi più interessanti che hanno caratterizzato l’attività solare nell’ultimo mezzo millennio: il minimo di Maunder. La sua precisione diminuisce, infine, man mano che ci si spinge indietro nel tempo. Detto in altri termini mentre la serie SN dà ottimi risultati per il periodo che va dal 1849 ai giorni nostri, offre il fianco a numerose critiche per il passato più remoto in quanto le osservazioni, in tali epoche, venivano effettuate senza tener conto dei criteri stringenti che hanno caratterizzato la serie di Wolf e dei suoi successori.

Per cercare di porre rimedio a questo stato di cose Hoyt e Schatten  nel 1998 hanno proposto di procedere al calcolo di un nuovo indice solare che tenesse conto non delle singole macchie solari, ma dei gruppi di macchie solari. Questo metodo consente di aggirare un grosso problema: i primi telescopi o gli altri metodi di osservazione del Sole utilizzati prima del 1749, non erano in grado di risolvere le singole aree che ospitavano macchie solari se non in casi molto particolari. Contando non più le singole macchie, ma i gruppi di macchie, si poteva ottenere una serie di indicatori molto più coerente della serie SN.

Il nuovo metodo di conteggio consentiva di calcolare un Numero di Gruppo (GN) che è diverso da SN. Tra i due indici esiste, però, una corrispondenza di proporzionalità diretta: il coefficiente di proporzionalità è pari a 12,08 ed è stato calcolato utilizzando i periodi di sovrapposizione tra la serie GN e la serie SN. Ad onor del vero tale proporzionalità non riguarda tutto il dataset, ma larga parte di esso e ciò è fonte di incertezza ed imprecisione per alcuni periodi (divergenza delle serie). Clette et al., 2014 si propone di eliminare proprio questa discrepanza tra le due serie di dati.

Per il calcolo dell’indice GN Hoyt e Schatten si sono serviti di lastre fotografiche del disco solare impressionate presso l’Osservatorio Reale di Greenwich che coprono il periodo che va dal 1874 al 1995 integrate dai disegni di tutte le serie classiche e di quelli di cui, nel corso dei decenni, gli studiosi sono riusciti ad entrare in possesso. La serie GN è un composito che tiene conto di serie di dati che erano sconosciute a Wolf e che consentono di  estendere il calcolo della serie SN, come derivato della serie GN, (annuale, mensile e giornaliera) fino al 1610. In particolare Hoyt e Shatten sono riusciti a recuperare dati osservativi che per il periodo compreso tra il 1610 ed il 1750 riescono a coprire 237 giorni con una media di cinque giorni di osservazione all’anno che presentano, però, significative dispersioni.

Particolarmente intensa è stata l’osservazione del Sole durante il minimo di Maunder: sommando le osservazioni con segnalazione di macchie solari e quelle che non registrano macchie solari, si riesce a coprire quasi il 98% del periodo del Grande Minimo.

Oggi come oggi si dispone, pertanto, di due serie di indici: uno basato sul numero di macchie solari (SN), l’altro basato sul numero di gruppi di macchie solari (GN). Le due serie hanno i pregi ed i difetti che abbiamo già individuato. Esse riescono, però, a ricostruire oltre quattrocento anni di attività solare. La serie GN è molto efficace per ricostruire i periodi più antichi, quella SN per ricostruire i periodi più recenti. Esse allo stato attuale dell’arte appaiono, però, divergere per cui si rende necessario rivisitarle per eliminare le divergenze.

Clette et al., 2014 cerca di ottenere questo risultato operando una serie di analisi e test statistici sulle due serie che cercherò, nei limiti delle mie possibilità, di sintetizzare nel seguito del presente articolo.

Gran parte di Clette et al., 2014 si basa su lavori di revisione pubblicati nel corso degli anni. Vari studiosi hanno, infatti, pubblicato i risultati di manoscritti inediti, disegni, tavole e note che hanno consentito di migliorare e correggere la prima versione della serie GN. Il risultato più importante di questa revisione è stato quello di individuare un inizio del ciclo di Maunder molto diverso da quello che si pensava. Secondo la linea di pensiero principale il minimo di Maunder iniziò dopo una serie di massimi molto forti ed in modo improvviso. La revisione degli studi effettuata recentemente dai ricercatori, ha consentito di stabilire che il ciclo solare precedente al Grande Minimo, fu un ciclo piuttosto debole per cui il passaggio al Grande Minimo non fu improvviso, ma graduale.  Altre correzioni hanno interessato periodi successivi al minimo di Maunder e sono state dettate dalla scoperta di manoscritti e documenti prima sconosciuti.

Una forte correzione riguarda anche il periodo relativo alle prime decadi del 1700: alcuni documenti sembravano confermare cicli solari piuttosto anomali e molto deboli. Documenti scoperti recentemente consentono, invece, di individuare valori di GN di tutto rispetto. Sono stati individuati, infine, problemi metodologici nelle osservazioni effettuate in questo particolare periodo storico. Nei resoconti di osservazioni fatte con linee meridiane (sorta di camere oscure che consentono l’osservazione del moto del Sole e la misura dei parametri che lo caratterizzano) o con telescopi meridiani, non si trova traccia di macchie solari. Documenti coevi, invece, testimoniano l’esistenza di macchie solari. I ricercatori che si sono occupati del caso reputano che le osservazioni meridiane non avevano ad oggetto l’individuazione di macchie solari per cui non se ne trova traccia nei resoconti ufficiali dati alle stampe. Nei manoscritti si parla, invece, di macchie solari. Il combinato disposto di queste circostanze porta a concludere che, contrariamente a quanto riportato nelle serie originarie dell’indice GN, l’ampiezza dei cicli solari in alcuni periodi deve essere rivista al rialzo.

A proposito di linee meridiane ancora esistenti, è celebre la linea meridiana realizzata nella cattedrale di S. Petronio a Bologna da Gian Domenico Cassini nella seconda metà del 1600: è lunga ben 66,8 metri ed occupa l’intera basilica; è la linea meridiana più lunga al mondo. Il foro gnomonico si trova a oltre 27 metri di altezza e la linea meridiana fu calcolata in modo da compensare l’inclinazione dell’asse della cattedrale rispetto alla direzione nord-sud: essa passa, infatti, tra le colonne e rappresenta uno strumento astronomico  di altissima precisione che consegnò G. D. Cassini alla storia.

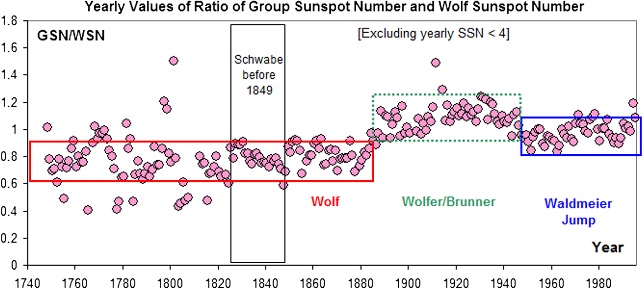
Passiamo ad esaminare ora alcune divergenze significative tra le serie GN ed SN determinate in modo statistico. Diversi studi hanno individuato un’anomalia statistica intorno al 1848. Si ricorderà che Wolf, sulla base dei risultati delle osservazioni nel periodo in cui le proprie si sovrappongono a quelle di Schwabe, aveva esteso la correzione effettuata per il periodo di sovrapposizione anche al periodo precedente il 1848. Studi successivi sembra che dimostrino che tale correzione sia da eliminare, ma altri studi tenderebbero a confermarla, ci troviamo, quindi, di fronte ad un problema che merita di essere ulteriormente approfondito.

Altri periodi che lasciano perplessi gli studiosi sono quello successivo al 1880 e quello successivo al 1945. Effettuando un confronto tra la serie SN e quella GN si vede che il rapporto statistico (ratio) tra le due serie presenta un brusco salto intorno al 1880 ed un altro salto (di segno opposto) intorno al 1945. Questi due anni rappresentano i punti di passaggio tra la gestione Wolf e la gestione Wolfer del conteggio SN (il primo) e la gestione Brunner e quella Waldmeier (il secondo).

Nel primo caso ci troviamo di fronte all’introduzione del coefficiente correttivo 0,6 per tener conto del fatto che i telescopi più potenti sopravvalutavano il conteggio rispetto a quelli più piccoli; nel secondo caso all’introduzione della ponderazione delle macchie in base alla loro grandezza. Si può pensare, pertanto, che esistano degli errori sistematici che rendono le due serie divergenti.

Tali errori sistematici non possono che essere ricercati nei coefficienti correttivi applicati ai dati grezzi. Nel grafico seguente (tratto da Clette et al., 2014, fig. 17) è illustrato quanto scritto nelle righe precedenti

Per poter risolvere il problema Clette et al, 2014 ha fatto ricorso ad un complesso processo di omogeneizzazione che ha coinvolto tutte le serie di dati disponibili.

Il metodo di omogeneizzazione utilizzato si basa sulle cosiddette “spine dorsali” (backbone). Tale metodo consiste nel confrontare le serie di dati relativi al Numero di Gruppo e quelli relativi al Numero di Wolf (SN) nei periodi in cui si sovrappongono determinando i relativi coefficienti di omogeneizzazione in modo che i valori del numero di gruppo e quelli del numero di Wolf, a meno del coefficiente di corrispondenza 12,08 coincidano. Il processo, ovviamente, è molto più complesso di quanto sembrerebbe dalla mia descrizione sommaria (si veda l’articolo originale pag. 58 e segg.), ma consente, a mio giudizio, di ottenere dei risultati soddisfacenti.

Sulla scorta di questa metodologia sono state individuate tre spine dorsali significative: la Schwabe, la Wolfer e la Koyama (dal nome dell’astronoma M. Koyama che ha diretto l’Osservatorio di Tokyo per decenni).

Il confronto tra la backbone di Schwabe, compresa tra il 1826 ed il 1867, e la serie GN ricostruita sulla base degli ultimi documenti ritrovati dimostra che esse sono coerenti per cui appare forzata l’applicazione del coefficiente correttivo proposto da Wolf per il periodo precedente al 1849.

Il confronto tra la backbone di Wolfer e la serie dei numeri di gruppo desunti dalle lastre fotografiche dell’Osservatorio Reale di Greenwich  ha consentito di accertare che effettivamente Wolfer aveva visto molte più macchie di quelle viste da Wolf in quanto la serie di Wolfer è del tutto coerente con quella di Hyott e Schatten (numeri di gruppo). Il confronto ha consentito di appurare che il rapporto tra la backbone di Wolfer e la serie di GN non è costante: varia in modo quasi continuo fino agli anni 90 del 19° secolo per poi stabilizzarsi. Ciò significa che la discontinuità rilevata intorno al 1882/1885 deve essere attribuita alle riduzioni apportate alle misure di Wolfer per adeguarle a quelle di Wolf.

La discontinuità intorno al 1945 è stata spiegata mediante il ricorso alla dorsale di Koyama e deve essere attribuita agli algoritmi di omogeneizzazione utilizzati dall’osservatorio di Zurigo durante la gestione Waldemeier. Tale algoritmo prevedeva la “pesatura” dei dati per tener conto dell’estensione delle macchie solari. Considerando che la correlazione tra la backbone di Koyama e la serie di Wolfer è elevatissima (R²=0,9952) dobbiamo dedurre che Wolf ha sottovalutato il numero di macchie solari e, quindi, il valore di SN a causa dell’uso del suo piccolo telescopio palmare. I valori da lui determinati, per essere confrontati utilmente alle serie di Shcatten e Hyott, devono essere incrementati quasi del 50%.

E’ in atto, infine, la creazione di una quarta backbone relativa al periodo 1749-1792  basata, essenzialmente sulla serie di Staudach confrontata con quelle di altri osservatori di cui si conoscono i rilievi delle macchie solari.

L’insieme di tutte queste elaborazioni numeriche ha generato la formazione di un composito dei numeri di gruppo omogeneizzato con i numeri di Wolf  e rappresentato nella immagine seguente.

Tale composito è stato oggetto di confronto con la ricostruzione dei cicli solari effettuata sulla base di numerosi dati di prossimità: deviazione diurna della componente orientale del campo geomagnetico, con la serie di Zurigo e con altri indicatori geomagnetici. Il confronto ha evidenziato problemi con il ciclo 7 (massimo nel 1830) e con il ciclo 10 (massimo nel 1860). Le ragioni di queste differenze devono essere ancora capite e saranno oggetto di ulteriori ricerche.

Questo è a grandi linee il lavoro che Clette et al, 2014 ha effettuato sulle due grandi serie di indici dell’attività solare oggi esistenti e, per quel che può valere, mi sembra un ottimo lavoro basato esclusivamente sulle osservazioni solari senza interpolazioni, estrapolazioni ed ammennicoli vari. La statistica è servita solo ed esclusivamente ad individuare incongruenze tra diverse serie di dati osservativi, ma non ha aggiunto nulla a ciò che già esisteva.

Con questo siamo, più o meno, a metà del lavoro di Clette et al., 2014. Il resto dello studio riguarda le disomogeneità emerse nel periodo successivo al 1950. Queste disomogeneità non sono affatto da trascurare in quanto determineranno delle modifiche a tutta la serie ricostruita nel modo illustrato nei paragrafi precedenti: l’armonizzazione tra la serie dei numeri di gruppo e quella dei numeri di Wolf procede a ritroso nel tempo per cui dobbiamo attenderci ulteriori novità.

A partire dal 1936 presso l’Osservatorio di Zurigo cominciò a manifestarsi la tendenza a modificare il metodo di conteggio usato fino ad allora. Sembrava più corretto pesare il numero di Wolf sulla base dell’estensione delle macchie solari. Wolf attribuiva ad ogni macchia il valore 1 indipendentemente dalle sue dimensioni ed escludeva dal conto i pore. Secondo la nuova linea di pensiero come si pesavano i gruppi di macchie solari, era necessario pesare anche le macchie singole in funzione della loro grandezza. Intorno alla metà degli anni 40 del ventesimo secolo la conversione alla nuova linea di pensiero poteva considerarsi completa almeno a Zurigo, ma non presso gli osservatori corrispondenti. Confrontando i numeri di gruppo con le serie dei numeri di Wolf dopo il 1945 si nota un salto che denota una sopravvalutazione del valore atteso del numero di Wolf di circa il 20%. Stesso risultato si ottiene confrontando la serie di Zurigo con gli spettroeliogrammi rilevati per il periodo 1915-1985 dall’osservatorio di Monte Wilson e che sono correlati con l’indice SN (R²=0,80). Analoga sopravvalutazione è indicata anche da altri dati di prossimità dell’attività solare legati al campo geomagnetico e ad altri indicatori.

Questa indagine ha portato Clette et al., 2014  a suggerire una correzione dei numeri di Wolf dei cicli successivi al 1947 di circa il 20% (relativamente ai valori caratterizzanti il massimo solare) per eliminare l’influenza dei fattori di ponderazione. E’ necessario precisare che altri studi fissano tale coefficiente al 12% per cui anche in questo caso dobbiamo parlare di lavori in corso.

Particolarmente interessante il complesso lavoro di revisione degli ultimi cinquant’anni di osservazione delle macchie solari. A prima vista sembrerebbe inutile concentrarsi su periodi in cui le osservazioni di un unico oggetto (la superficie del Sole) dovrebbero essere standardizzate ed omogenee. La cosa non è, invece, così semplice in quanto i risultati delle operazioni di rilievo sono abbastanza aleatori. Le osservazioni sono, infatti, eseguite da uomini e, pertanto, risentono di una certa soggettività. Se prendiamo ad esempio la stazione di Locarno, notiamo che il numero di Wolf della stazione tende a ridursi con il tempo e, dopo una certa data, comincia a risalire. La cosa potrebbe essere attribuita a  fattori collegati con la fisica solare, ma, molto più prosaicamente, dipende dall’invecchiamento dell’osservatore, dal degrado delle sue capacità visive e dalla modifica delle condizioni al contorno dell’osservatorio. Detto in altri termini ogni stazione di rilevamento può manifestare delle derive che portano a errori sistematici nella determinazione dei parametri rilevati. Anche il cambio del telescopio genera, infine, polarizzazione nei risultati.

Questo fatto richiede la rideterminazione dei valori dell’indice SN per tutto il periodo di osservazione moderno (successivo al 1940) per eliminare ogni possibile fonte di errore sistematico nelle misurazioni eseguite. Tale ricalibrazione del calcolo dei valori dell’indice SN non è, però, una cosa semplice in quanto richiede una metodica di ricalcolo ancora tutta da costruire e sulla quale gli studiosi sono ancora al lavoro.  La cosa è complicata anche dal fatto che negli ultimi decenni sul Sole si stanno manifestando dei cambiamenti che possono elidere o rafforzare gli errori sistematici commessi dagli osservatori a terra. Sembra che la magnetosfera solare sia soggetta a variazioni che stanno alterando la struttura delle macchie solari: diminuisce il numero di macchie grandi e aumenta quello delle macchie di piccole dimensioni. Poiché i parametri per il calcolo dell’SN tengono conto anche delle dimensioni delle macchie, si capisce che questo fatto determina anche errori nel calcolo del numero di Wolf.

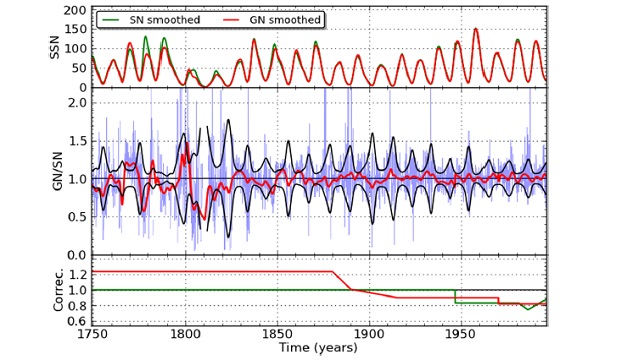
A conclusione di questa lunga, ma non esaustiva, disamina dell’imponente lavoro riassunto in Clette et al., 2014 possiamo dare un’occhiata al grafico seguente che, per gli ultimi 250 anni, mette a confronto le serie dei numeri di gruppo e dei numeri di Wolf dopo le correzioni apportate e sommariamente descritte in questo articolo.

Per armonizzare le due serie di dati si è provveduto ad applicare ai dati omogeneizzati i coefficienti correttivi indicati nel terzo riquadro (ultimo in basso). Il riquadro intermedio dimostra che, dopo le correzioni effettuate, il rapporto GN/SN è praticamente costante a partire dai primi decenni del 19° secolo, mentre si notano ancora delle incertezze per il periodo compreso tra il 1749 ed il 1820.

Dall’esame dei diagrammi SN e GN si evince che l’ampiezza dei cicli del 20° secolo non ha nulla di eccezionale essendo del tutto confrontabile con quella del 18° secolo e del 19° secolo. Ciò che rende unico il 20° secolo, dal punto di vista dei cicli solari, è la fortissima concentrazione di cicli molto intensi: mai negli ultimi 250 anni e forse negli ultimi 400 anni, si è verificata una serie di cicli intensi così lunga.

Essendo le emissioni di energia da parte del Sole collegata all’intensità dei cicli solari, possiamo dedurne che l’influenza del Sole sul clima terrestre potrebbe essere rappresentata non dall’eccezionale intensità dei cicli solari, ma dall’eccezionale numero di cicli solari intensi che si sono succeduti. L’inerzia del sistema climatico terrestre ha fatto il resto.

Una nota curiosa. Guardando il grafico, non ho potuto fare a meno di notare che i cicli intensi e quelli deboli si succedono in forma apparentemente periodica: sei cicli deboli e sei forti. Considerando che il ciclo medio dura circa 11 anni, ci troviamo di fronte ad un numero piuttosto ricorrente in ambito climatologico: circa 60. E’ una coincidenza?

Questo articolo mi è parso importante per una molteplicità di motivi: il clima, il Sole, il metodo scientifico, la storia della scienza, ma anche e soprattutto per due ragioni che inglobano una o più delle motivazioni che ho elencato.

La prima riguarda le serie di dati storiche ed i processi di omogeneizzazione di cui tante volte ci siamo occupati. Molte volte ci scandalizziamo quando si modificano i dati del passato. Raramente pensiamo a come sono state costruite queste serie di dati, al modo in cui si sono assemblati dati rilevati da operatori diversi, con strumenti diversi, con metodologie diverse.

La seconda ragione riguarda l’oggetto dell’osservazione: il Sole. Il Sole è unico, in uno stesso giorno le macchie da contare dovrebbero essere le stesse da qualunque punto le si guardi. Invece mi sono trovato di fronte ad una serie di dati in contrasto tra loro a causa della soggettività dell’osservatore e della strumentazione usata. Per me è stata una constatazione sorprendente che mi ha profondamente meravigliato.

Non ho potuto fare a meno, a questo punto, di pensare alle serie di temperature globali elaborate da NOAA, GISS, Hadley Center, ecc. ed alle classifiche di anni caldi e freddi. In questo caso noi non misuriamo grandezze riferite ad un unico oggetto, ma grandezze relative ad una moltitudine di oggetti: le temperature dei vari siti ove sono ubicate le centraline di rilevazione. Se ognuna di queste grandezze è affetta da una percentuale delle problematiche che caratterizzano la misura del numero di Wolf e questa percentuale la si estende a tutte le innumerevoli misure effettuate, che attendibilità scientifica può avere il loro prodotto, ovvero la temperatura globale? In ognuna di queste centraline sono cambiati, nel corso del tempo, gli operatori, gli strumenti, le condizioni al contorno, tutto in altri termini. In occasione del cambio degli strumenti di misura si sono previsti periodi di sovrapposizione per individuare bias polarizzanti di natura strumentale? E’ stato fatto lo stesso quando sono cambiate le condizioni al contorno? Da quello che mi risulta l’omogeneizzazione avviene soprattutto se non esclusivamente da un punto di vista statistico e ciò mi rende oltremodo perplesso. Mi sa che quando parliamo di parametri  globali stiamo parlando di qualcosa che assomiglia molto al sesso degli angeli.

Nel futuro lo faremo ancora, ma quando lo faremo cerchiamo di pensare per un attimo a ciò di cui stiamo parlando. Mi auguro, infine, che lo stesso ragionamento facciano coloro che prendono quei numeri al centesimo di grado centigrado come oro colato e ci costruiscono politiche socio-economiche che coinvolgono miliardi di persone.