Chi segue il dibattito che si è sviluppato intorno alle problematiche del riscaldamento globale e del cambiamento climatico ha ormai piuttosto chiari i termini della discussione. Ciò che non è chiaro, invece, è la fisica del problema cioè l’individuazione delle cause che determinano il cambiamento climatico e l’elaborazione di un modello fisico-matematico che consenta di prevedere l’evoluzione del clima terrestre. La linea di pensiero principale è quella basata sui report dell’IPCC e, quindi, sugli output dei grossi modelli di circolazione globale che attribuiscono la responsabilità del cambiamento climatico alla concentrazione di CO2 nell’atmosfera terrestre.
Altri studiosi sono dell’avviso, invece, che il clima è regolato da meccanismi molto più complessi che i modelli di circolazione globale non sono in grado di replicare: questo gruppo minoritario di studiosi si presenta, al suo interno, piuttosto variegato. Alcuni sono dell’avviso che siano i cicli solari a guidare il sistema climatico terrestre, altri sostengono che il clima terrestre sia regolato da un mix di fattori antropici ed endogeni che ancora non siamo in grado di comprendere appieno, altri sono dell’avviso che le attuali modificazioni climatiche rientrano in quelle che sono le oscillazioni naturali del sistema stesso.
Nelle scorse settimane abbiamo avuto modo di parlare qui e qui di due lavori che individuavano una relazione tra i cicli solari e le temperature terrestri (emisferiche nel primo caso). Molti studiosi faticano, però, ad accettare i risultati di questi lavori. Sul blog WUWT, per esempio, si considera quasi scontato che i cicli solari non sono in grado di determinare il clima terrestre. Altri studi (Pasini et al., 2012, per esempio) trovano una relazione tra alcune grandezze legate al Sole e le temperature terrestri fino agli anni ’50 del secolo scorso che, però, si perde nei decenni successivi.
Un esempio emblematico della discussione che anima la comunità scientifica su questi temi, è rappresentata da due lavori pubblicati recentemente e che è mia intenzione commentare brevemente.
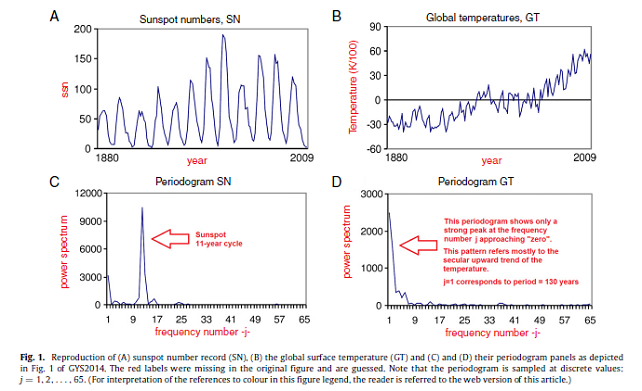
Un primo lavoro che individueremo da ora in avanti con Gil-Alana et al., 2014 (qui l’abstract) alla domanda che costituisce il titolo di questo post fornisce una risposta negativa. Riassumo brevemente Gil-Alana et al., 2014. Gli autori dello studio hanno preso in esame un set di dati delle temperature globali terrestri (GISS, per la precisione) ed il record storico dell’indice SSN (un indice che tiene conto del numero delle macchie solari e che consente di stabilire la lunghezza del ciclo solare). A queste serie di dati hanno applicato delle metodologie di analisi statistiche elaborate in ambiti diversi e perfezionate, successivamente, in econometria per analizzare serie di dati economico-finanziari. Il concetto posto alla base di tali metodiche è quello di “memoria lunga” che esprime l’idea che le misurazioni di grandezze caratterizzanti un fenomeno fisico non sono tra loro indipendenti, cioè, i valori assunti in precedenza da una grandezza fisica, sono in grado di influenzare i valori successivi della stessa grandezza anche se in modo tale che, con il passare del tempo, tende a smorzarsi. In altri termini dati apparentemente aleatori, in realtà, presentano una qualche regolarità. La metodologia sommariamente descritta trova le sue applicazioni d’elezione per serie di dati di tipo stazionario, indipendenti, cioè, dal tempo. In questi casi è possibile individuare quella che si definisce una funzione di densità spettrale e disegnarne il periodogramma che, in ascissa, presenta il numero di frequenza o la frequenza ed in ordinata la potenza del periodo corrispondente.
Gil-Alana et al., 2014, hanno applicato ai due record di dati l’analisi di Fourier discreta. La trasformazione così effettuata ha consentito il passaggio dal dominio del tempo a quello delle frequenze ed ha consentito di ottenere, alla fine, le funzioni di densità spettrale. Per quel che riguarda il record SSN, il diagramma di densità spettrale presenta un massimo in corrispondenza del periodo di 11 anni che coincide con il classico ciclo solare circa-undecennale. La deduzione logica è che il record SSN è rappresentabile mediante un modello frazionario ciclico.
Per quel che riguarda la serie di temperature il discorso è un po’ più articolato. Le temperature globali, infatti, sono non stazionarie in quanto presentano un trend, sono, cioè, dipendenti dal tempo (dal 1880 ad oggi esse sono aumentate secondo un trend che gli autori hanno supposto lineare). In questo caso l’applicazione dell’analisi di Fourier discreta ha consentito di ottenere un periodogramma che presenta un massimo in corrispondenza del punto di ascissa 1 (periodo di circa 130 anni). Ciò comporta che per tale serie di dati sembra ragionevole, per gli autori, applicare un modello frazionario integrato (in gergo statistico I(d)).
Ebbene, confrontando tali funzioni di densità spettrale essi hanno visto che il periodogramma dell’SSN e quello delle temperature presentano due massimi: la funzione delle densità spettrali del record SSN presenta un massimo in corrispondenza del numero di frequenza 12 (ciclo solare undecennale), mentre quella delle temperature presenta un picco in corrispondenza del punto di ascissa 1 (corrispondente ad un periodo di circa 130 anni) e nessun picco di ciclicità circa-undecennale.
Il fatto che le due serie di dati possano essere rappresentate da due modelli stocastici profondamente differenti e che presentino poli a frequenze diverse, secondo gli autori, non consente loro di rifiutare l’ipotesi nulla, ovvero che temperature globali e cicli solari non sono correlati e da ciò concludono che i due processi fisici modellati non sono correlati. Detto in altri termini Gil-Alana et al. 2014 sembra giungere alla conclusione che non esistendo correlazione tra i cicli solari e le temperature globali terrestri, il Sole non è in grado di determinare le variazioni delle temperature terrestri e, quindi, che l’aumento delle temperature globali registrato tra il 1880 ed il 2014 non può essere collegato alle dinamiche solari. La sentenza, come si vede, sembra senza appello.
Il dr. N. Scafetta non concorda con le conclusioni di Gil-Alana et al. 2014. Egli nel recentissimo articolo:
fornisce una risposta al quesito indicato nel titolo di questo post diversa da quella di Gil-Alana, 2014. La risposta del dr. Scafetta, come si deduce dal titolo del suo lavoro (da ora in avanti Scafetta, 2014), è positiva, ma con un piccolo dettaglio da tener presente: la relazione è di tipo non lineare. Ho parlato di dettaglio e, come tutti ben sanno, è proprio nei dettagli che si annida il diavolo.
Partiamo dalla figura 1 di Scafetta, 2014 e tratta da qui. In questa figura troviamo rappresentate le conclusioni di Gil-Alana et al., 2014 che ho sommariamente riportato in precedenza: i set di dati nel dominio del tempo ed i relativi periodogrammi ottenuti applicando l’analisi di Fourier discreta. L’illustrazione è quella originaria di Gil-Alana et al., 2014 integrata dal dr. N. Scafetta: si notino i picchi delle funzioni di densità spettrale calcolati con i due modelli numerici ed il fatto che non sono affatto coincidenti.
Scafetta, 2014 critica innanzitutto la scelta di Gil-Alana et al., 2014 di costruire i periodogrammi mediante l’analisi di Fourier discreta in quanto si ottengono risultati a bassa risoluzione. Tale metodica, inoltre, è in grado di generare degli artefatti di calcolo. Analizzando i due periodogrammi della figura 1, infatti, si nota che estrapolando il risultato a valori di j<1 si ottengono dei falsi picchi di potenza. In altri termini portando al limite il ragionamento si avrebbero delle singolarità per numeri di frequenza tendenti a zero. Ciò porta alla conclusione fallace che periodi aventi lunghezza maggiore della lunghezza delle serie prese in esame, abbiano potenza maggiore di quella di periodi di lunghezza inferiore a quella della serie di dati. Da notare, infine, che il picco di potenza spettrale del periodogramma delle temperature globali per j=1 è più accentuato di quello del periodogramma relativo alle macchie solari. La ragione di ciò, secondo Scafetta, 2014, deve essere ricercata nella più accentuata non stazionarietà della serie delle temperature globali.
Questa osservazione porta alla conclusione che le tecniche di analisi spettrale dovrebbero essere utilizzate con cautela quando si ha a che fare con serie di dati non stazionari come quelli relativi alle temperature globali. In ogni caso sarebbe opportuno procedere a tutta una serie di trattamenti statistici dei dati (filtraggi vari) per ricondurli alle condizioni di stazionarietà.
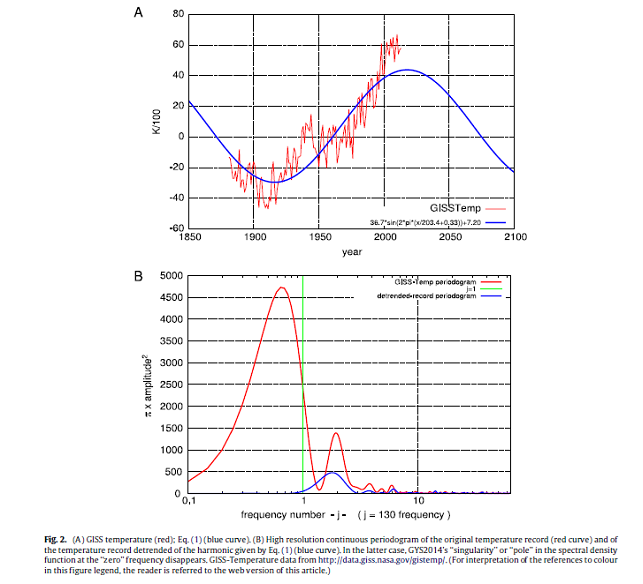
Successivamente Scafetta, 2014 procede ad un’elaborazione della serie di dati delle temperature globali mediante analisi di Fourier continua ottenendo il periodogramma in rosso nella seguente figura 2B tratta da qui. Scafetta, 2014 in questa figura ha utilizzato per i numeri di frequenza la scala logaritmica (per meglio evidenziare i picchi di potenza) ed ha evidenziato in verde il numero di frequenza pari ad 1 corrispondente al valore più piccolo individuato da Gil-Alana et al., 2014 per i numeri di frequenza dell’analisi di Fourier discreta.
Dall’esame della figura si vede che il periodogramma costruito con l’analisi di Fourier continua presenta un massimo in corrispondenza di j=0,66 e poi converge a zero per valori di j<0,66. Il massimo trovato, per quanto detto in precedenza, deve essere considerato il frutto di un’armonica spuria in quanto numeri di frequenze inferiori all’unità risultano illogici e statisticamente incoerenti. Esso è il frutto della non stazionarietà della serie di temperature. Eliminando l’armonica spuria per j=0,66 mediante un algoritmo che ha generato il fit armonico della figura 2A (curva in blu), si ottiene il periodogramma in blu nella figura 2B che rappresenta il periodogramma della serie di temperature globali privato del trend di aumento. Si noti che il periodogramma in blu della figura 2 presenta un picco di potenza per j=2: corrisponde ad un periodo di 60 anni. Anche nella serie GISS, pertanto, è presente una traccia del periodo di circa 60 anni che ricorre frequentemente nelle analisi statistiche delle serie di temperature. Da notare, infine, che è completamente sparito il picco di potenza in corrispondenza del numero di frequenza j=1: ulteriore dimostrazione che trattavasi di un artificio di calcolo legato alla non stazionarietà della serie delle temperature ed all’utilizzo dell’analisi di Fourier discreta.
Concludendo, Scafetta, 2014 è del parere che le conclusioni di Gil-Alana et al., 2014 sono illusorie in quanto frutto dell’applicazione dell’analisi di Fourier discreta, dell’unione mediante segmenti dei punti spettrali discreti e di estrapolazioni inappropriate dei risultati all’intervallo di numeri di frequenza 0<j<1.
Questo relativamente agli aspetti squisitamente statistici e matematici di Gil-Alana et al., 2014. Resta, tuttavia, il fatto che la serie delle temperature globali e la serie dell’indice SSN non sono correlati: tanto nelle analisi di Gil-Alana et al., 2014 che di Scafetta, 2014 sono assenti periodi di 11 anni nelle serie di temperature. Scafetta, 2014 in proposito fa notare che la relazione tra temperature terrestri e fenomeni solari sono molto più complesse del semplice confronto lineare impostato da Gil-Alana et al., 2014.
Per poter evidenziare delle relazioni tra l’attività solare ed il clima terrestre, infatti, bisogna considerare aspetti fisici che Gil-Alana et al., 2014 non prende assolutamente in considerazione, in quanto si limita solo ad una trattazione matematica di due serie di numeri. Dal punto di vista matematico, invece, è necessario utilizzare metodiche molto più sofisticate basate su algoritmi di filtraggio dei dati e su algoritmi di analisi spettrale più complesse dell’analisi di Fourier: Metodo della Massima Entropia (MEM), Metodo multi-taper (MTM), ecc..
Per quel che riguarda gli aspetti squisitamente fisici della questione, Scafetta, 2014, fa notare che l’azione del Sole sul clima terrestre è mediata da molti altri fattori tra cui anche il numero di macchie solari. Limitare l’attenzione solo all’indice SSN, pertanto, è riduttivo e poco significativo. A titolo di esempio Scafetta, 2014 cita alcuni suoi studi, di cui abbiamo parlato anche sulle pagine di CM, in cui dimostra che, applicando il metodo della massima entropia alla serie di temperature HadCRUT3, si evidenziano periodi molto forti che possono essere associati a particolari cicli solari ed a cicli astronomici.
Il ciclo delle macchie solari, inoltre, non deve essere considerato, come fa Gil-Alana et al., 2014, come l’unico indice dell’attività solare. La TSI (irradianza totale solare), per esempio, non è legata al ciclo delle macchie solari, ma presenta un andamento differente caratterizzato da periodi diversi dal ciclo solare undecennale classico (come discusso anche qui su CM). Non secondaria, inoltre, nel determinare l’andamento del clima terrestre è l’influenza antropica che incide sul riscaldamento globale, secondo il dr. Scafetta, per un’aliquota non trascurabile.
Anche il campo magnetico solare non è legato direttamente al ciclo solare undecennale, ma è influenzato da altri fattori e sembra implicato nella modulazione dei raggi cosmici galattici responsabili della nucleazione delle nuvole. In altri termini collegare linearmente il ciclo solare tramite l’indice SSN alle dinamiche solari ed alle loro influenze sul clima terrestre, come ha fatto Gil-Alana et al., 2014, non è corretto. Appare molto più corretto, invece, considerare il legame non lineare che esiste tra il Sole ed il clima terrestre e, in ultima analisi, tra il ciclo delle macchie solari e le temperature globali.
Non dimentichiamo, infine, i contributi di F. Zavatti che su CM ha per molti mesi fornito i periodogrammi della serie di temperature del NOAA, calcolati con il metodo della massima entropia, che hanno evidenziato numerosi periodi tra cui anche quello circa undecennale (qui uno dei suoi post, a mio giudizio, più interessanti). Nell’articolo del dr. N. Scafetta, ovviamente, molti altri sono gli spunti di riflessione e le citazioni di lavori scientifici che si sono occupati della problematica. Sviscerarli tutti equivarrebbe a ricopiare il suo articolo su queste pagine e, francamente, avrei l’impressione di sottovalutare l’intelligenza dei lettori di CM. Chi è interessato può leggere direttamente l’articolo qui.


Sii il primo a commentare