Dati NOAA e non solo, esempi di detrending

Stavo cercando di capire come utilizzare al meglio i dati NOAA della temperatura globale -medie mensili terra-oceano- disponibili alla pagina cosidetta “Climate at a glance” qui, che sostituisce il sito ftp da cui finora ho scarticato i dati mensili e mi sono trovato, quasi per casoi, a pensare cosa sarebbe successo al dataset con una serie di detrending successivi, cioè eliminando tutti i trend che potevo individuare, tramite un fit o in generale tramite una rappresentazione analitica, seguiti da una sottrazione (dati-fit) e ripetendoi il processo fino ad avere residui a media nulla e senza una struttura identificabile (qualcosa che potrebbe essere chiamato rumore, anche se potrà contenere strutture nascoste ad una semplice analisi visiva). Applicando questo schema ai dati noaa fino a gennaio 2014, ho trovato quello che mostro nella successiva Fig.1 (pdf).

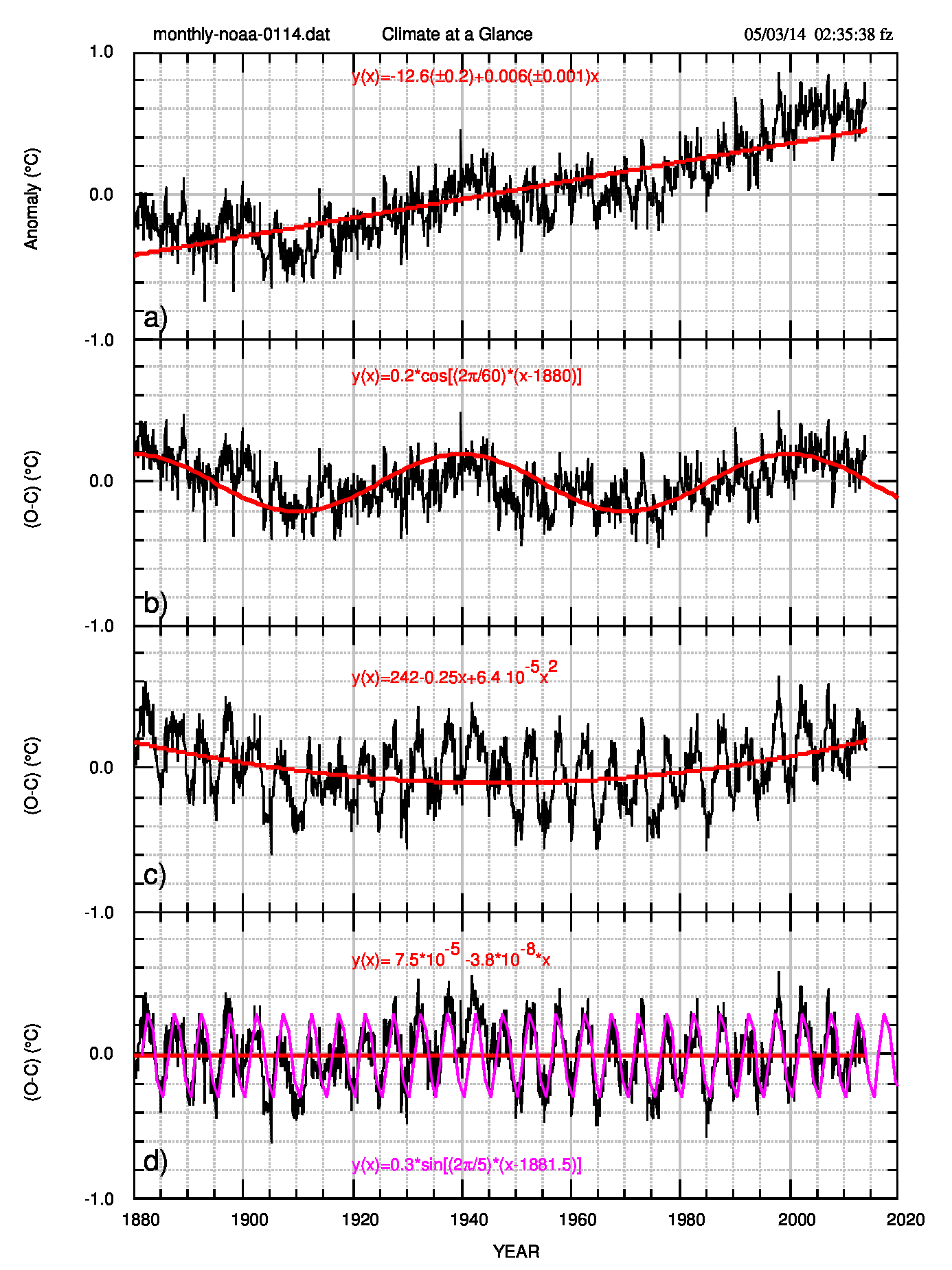
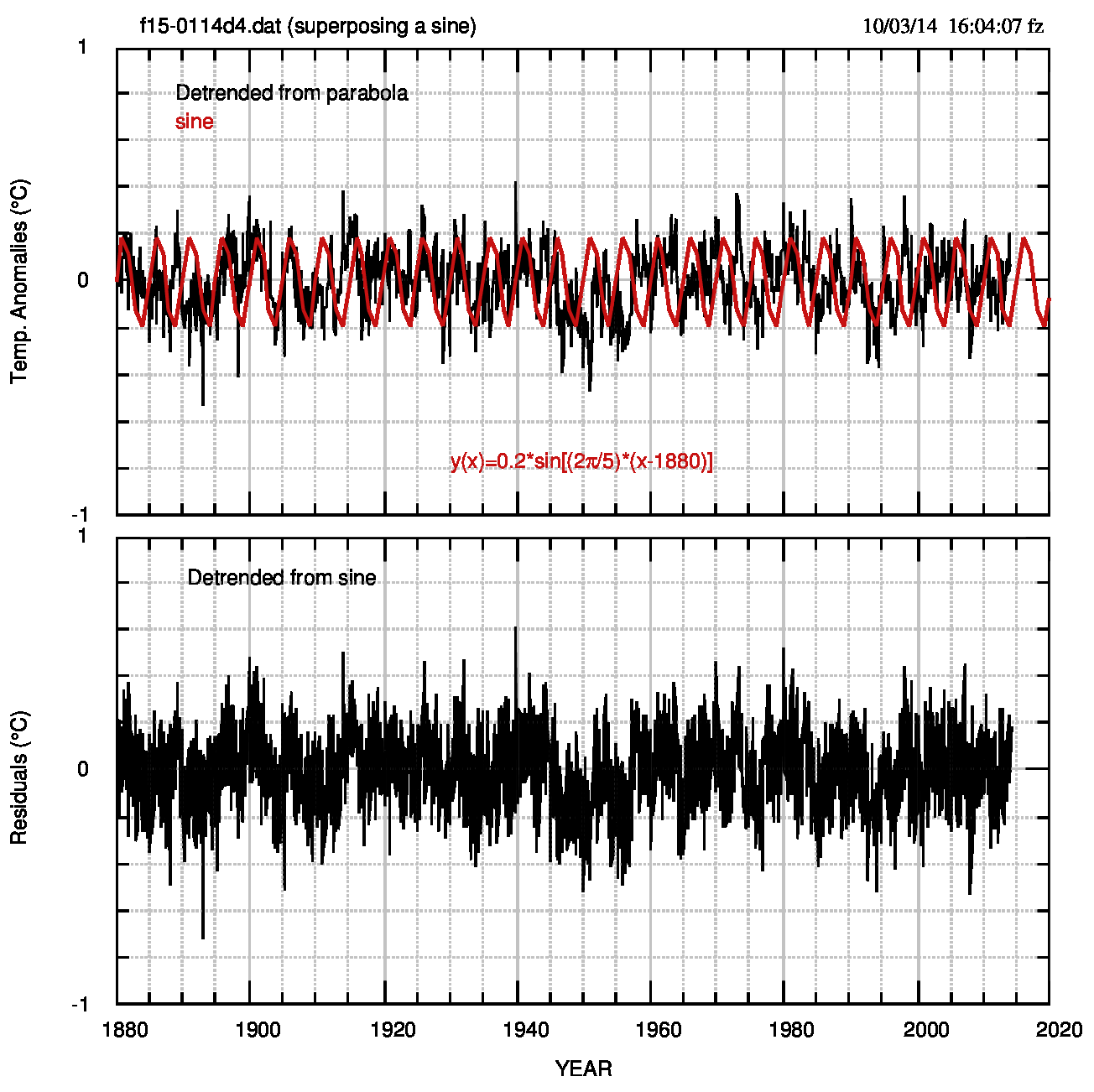
 Nel quadro a) il fit lineare dei dati iniziali noaa-0114; in b) i residui -il detrending- dalla retta e la rappresentazione di tali residui con una funzione sinusoidale. In c) il detrending dal coseno e il suo fit parabolico; in d) i residui dalla parabola e il loro fit lineare, con lo scopo di mostrare la media praticamente nulla degli ultimi residui. Nel quadro d), però,succede una cosa “strana”: la media è,sì, nulla ma resiste una struttura molto ben identificabile come un seno di periodo 5 anni. La curva fucsia che la rappresenta piuttosto bene è descritta dalla formula in basso in Fig.1.
Vorrei far notare che i termini “fit” e “rappresentazione” sono stati usati a ragion veduta: discuterò questo punto successivamente.
Ora, però, essendo ancora presente una struttura, si pone il problema del detrending dalla stessa (per la quale i fit non lineari tramite un seno e tramite un coseno forniscono risultati praticamente indistinguibili). Nella Fig.2 (pdf) viene mostrato il risultato del detrending da entrambe le sinusoidi.

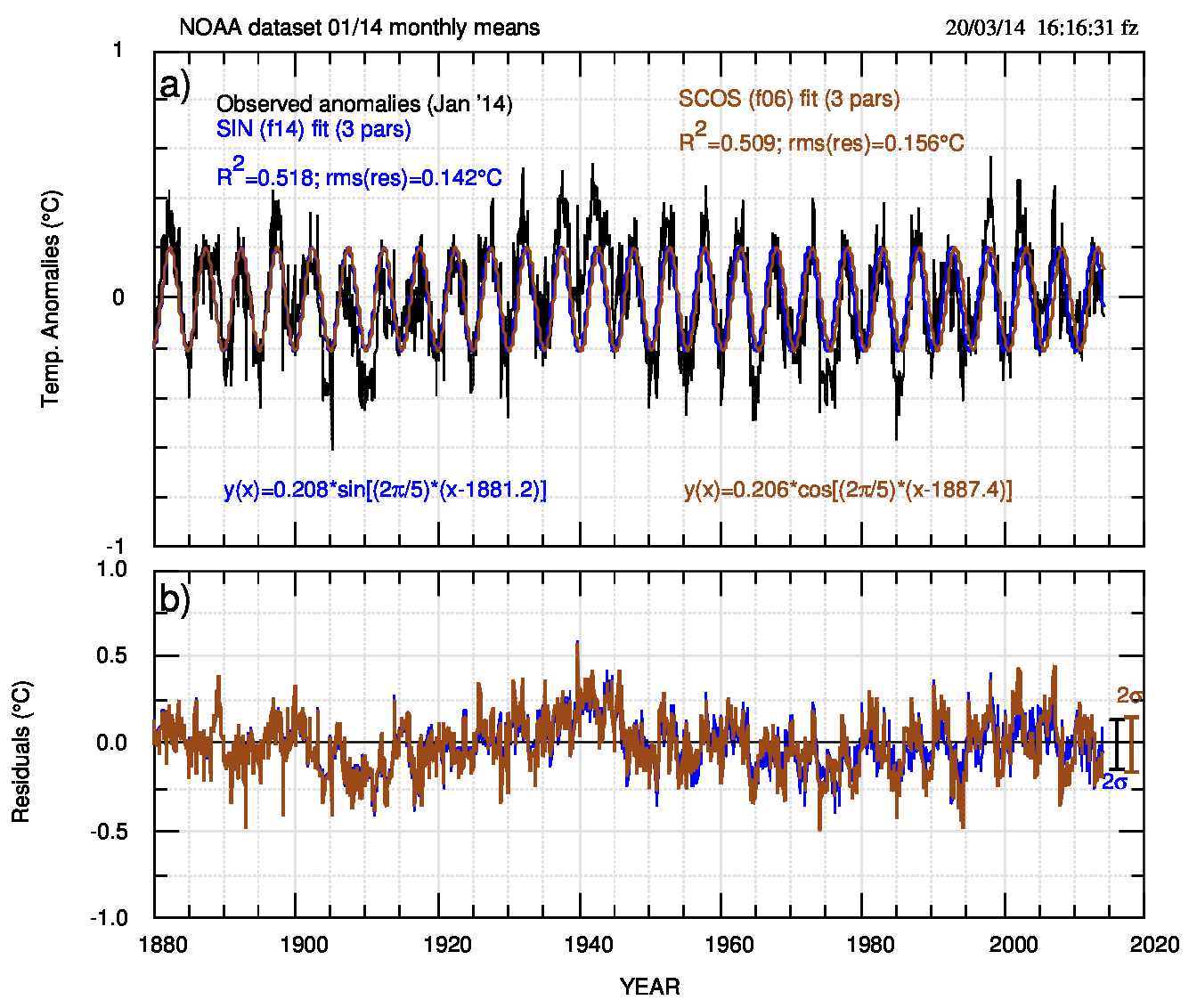
Nel quadro b) di quest’ultima figura si vede la persistenza di due strutture: una, più visibile, è un riscaldamento tra il 1910 e il 1945 e l’altra un riscaldamento tra il 1975 e il 1997. La prima ha un trend di (0.118±0.005)°C/10anni e la seconda di (0.05±0.01)°C/10anni. Entrambe mimano i corrispondenti riscaldamenti visibili nei dati originali ma con pendenze invertite: il secondo periodo “originale” ha una pendenza leggermente superiore a quella del primo (v.qui).

Se non fosse sbagliato, il risultato di Fig.2 sarebbe sorprendente: in primo luogo c’è una netta oscillazione di periodo 5 anni, mai vista prima; poi i due riscaldamenti (e il raffreddamento intermedio) che continuano ad essere presenti malgrado le funzioni analitiche che avrebbero dovuto intercettarli e quindi eliminarli; e, ancora, le pendenze diverse (una più del doppio dell’altra) che possono far pensare a meccanismi fisici diversi per i due warming (mentre nei dati osservati si può senz’altro ipotizzare lo stesso meccanismo).

Ma, come dicevo, il metodo usato finora è sbagliato e l’errore è proprio nella differenza tra “fit” e “rappresentazione”. Infatti il coseno di Fig.1 b) non è un fit ma una sinusoide i cui parametri sono stati ricavati da una serie di tentativi, così da rappresentare i dati in modo sufficientemente sensato. Anche per il seno del quadro d) si è seguita la stessa tecnica ma qui l’errore è meno importante (e c’è il confronto con i fit di Fig.2).

Il procedimento corretto è quello di calcolare matematicamente i parametri della funzione che rappresenta i dati e quindi ho ricalcolato i fit (questa volta solo fit e non rappresentazioni) e i detrending successivi e li mostro nelle Fig. 3 (pdf) e 4 (pdf).

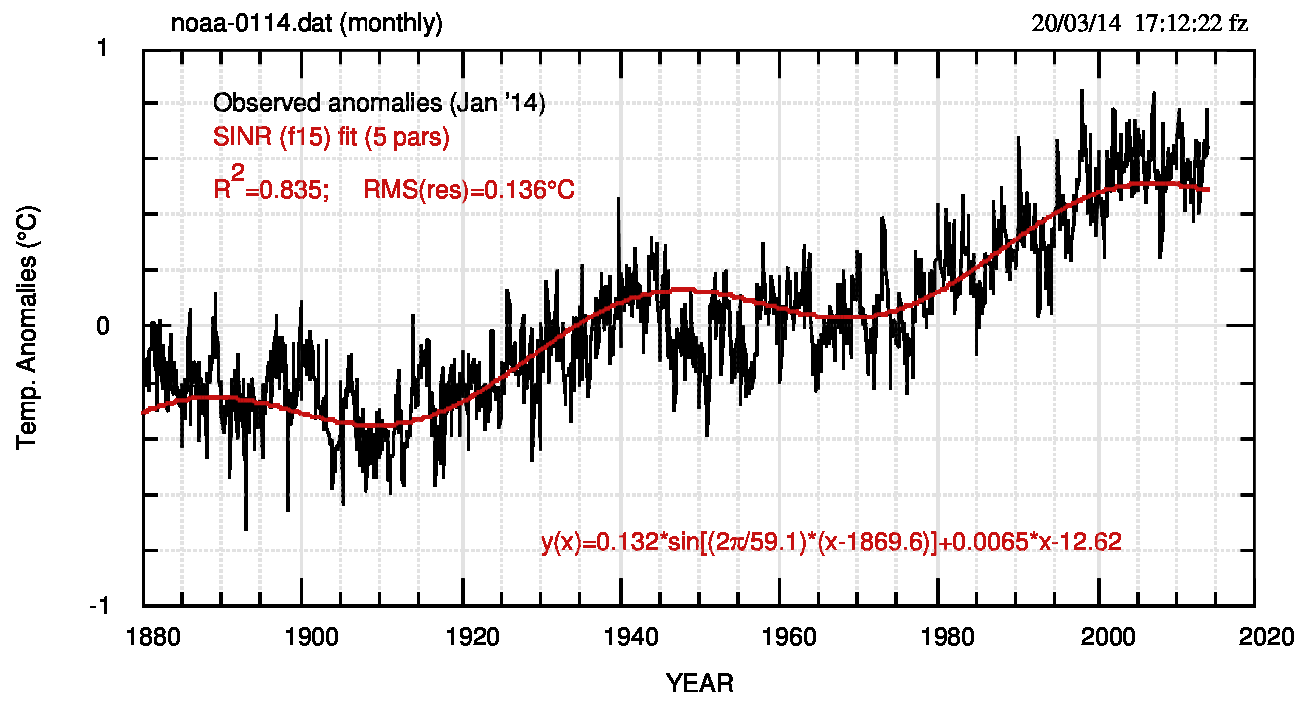
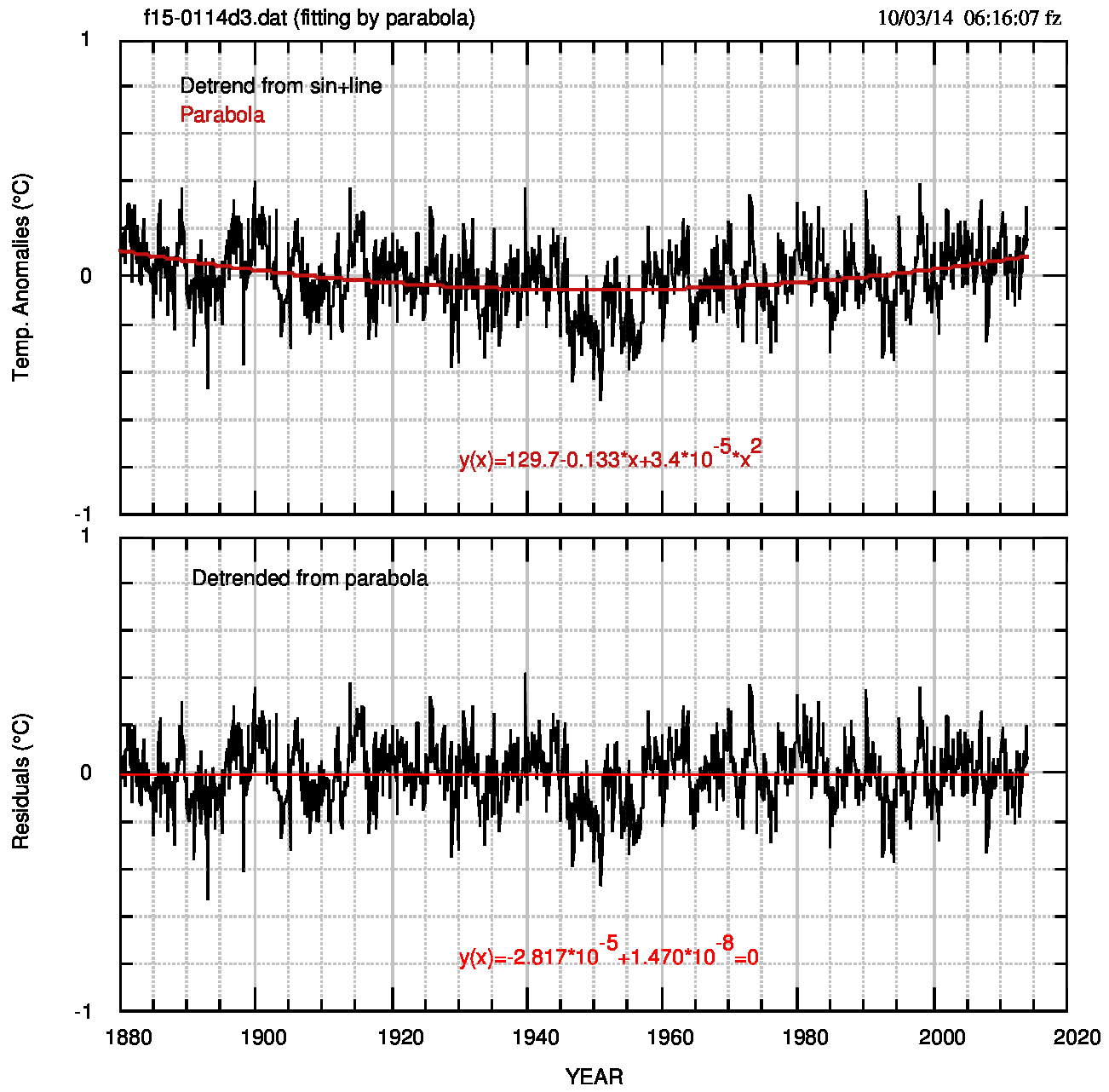
 Da notare in queste figure che i 5 parametri calcolati analiticamente differiscono poco dai 2+3 parametri (calcolati e fissati) di Fig.1 a) e b): da un massimo del 35% per le ampiezze a un minimo dell’1.5% per i periodi; valori sufficienti, però, per drastiche differenze nei risultati finali. I parametri della parabola differiscono dai precedenti (sempre calcolati) di circa il 46-47%, come effetto dei cambiamenti nel fit precedente. La media è ancora nulla e non si notano, nel quadro inferiore di Fig.4, strutture di particolare rilievo, anche se si possono vedere strutture di dimensione circa decennale, ad esempio attorno al 1910, al 1980 e al 1990.
Nella successiva Fig.5 (pdf)

c’è il tentativo di rappresentare con un seno a 5 anni i residui dal fit parabolico. Il tentativo è evidentemente maldestro e non si riesce a vedere come, cambiando la fase iniziale, le cose possano migliorare (forse cambiando il periodo, ma qui ci stiamo confrontando con la situazione precedente).
Gli spettri confermano le differenze tra un metodo (sbagliato) e l’altro (corretto). In Fig.6 (pdf) lo spettro dei residui finali di Fig.1; in Fig.7 (pdf) lo spettro dei residui finali di Fig.4.

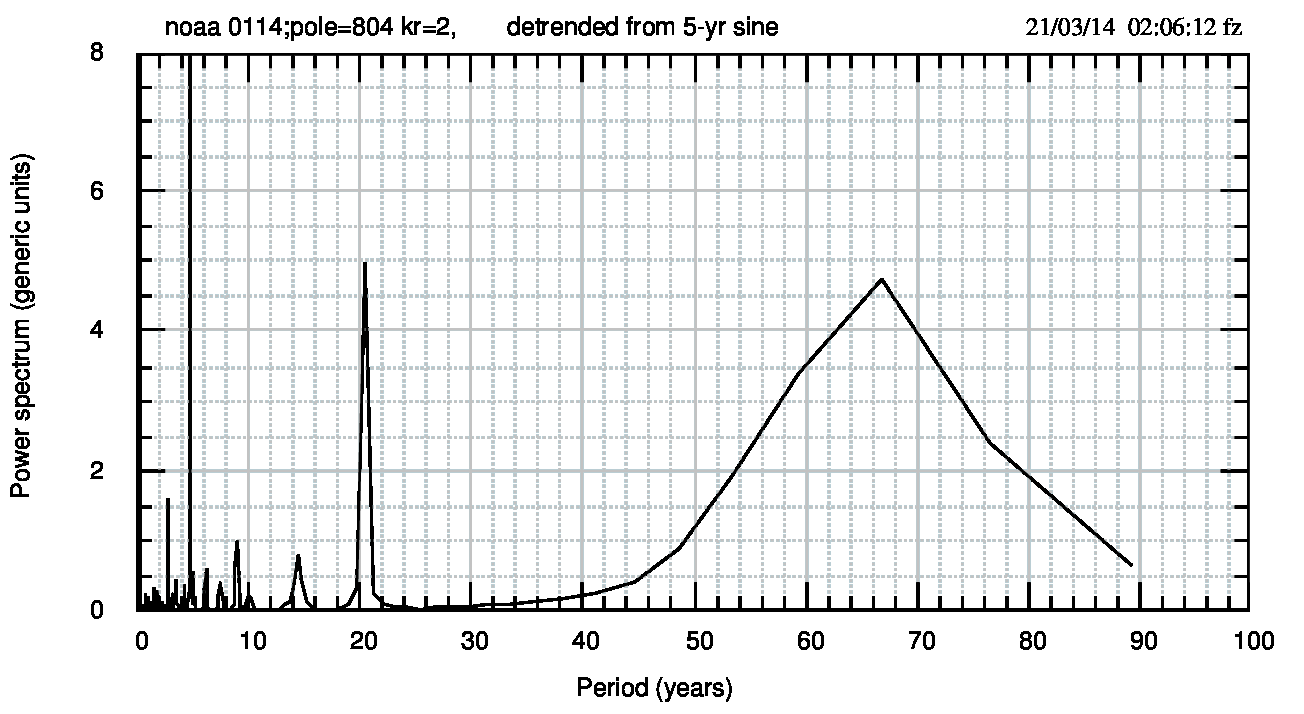
Questa figura mostra come il periodo 67 anni resista ai detrending (anche se la potenza diminuisce di circa il 30%) e come il periodo a 5 anni sia il più prominente, con una potenza di 198 sulla scala della figura, cioè più di 40 volte la potenza del picco a 20 anni. Quest’ultimo periodo è forte e non è stato intercettato dalle funzioni analitiche usate.

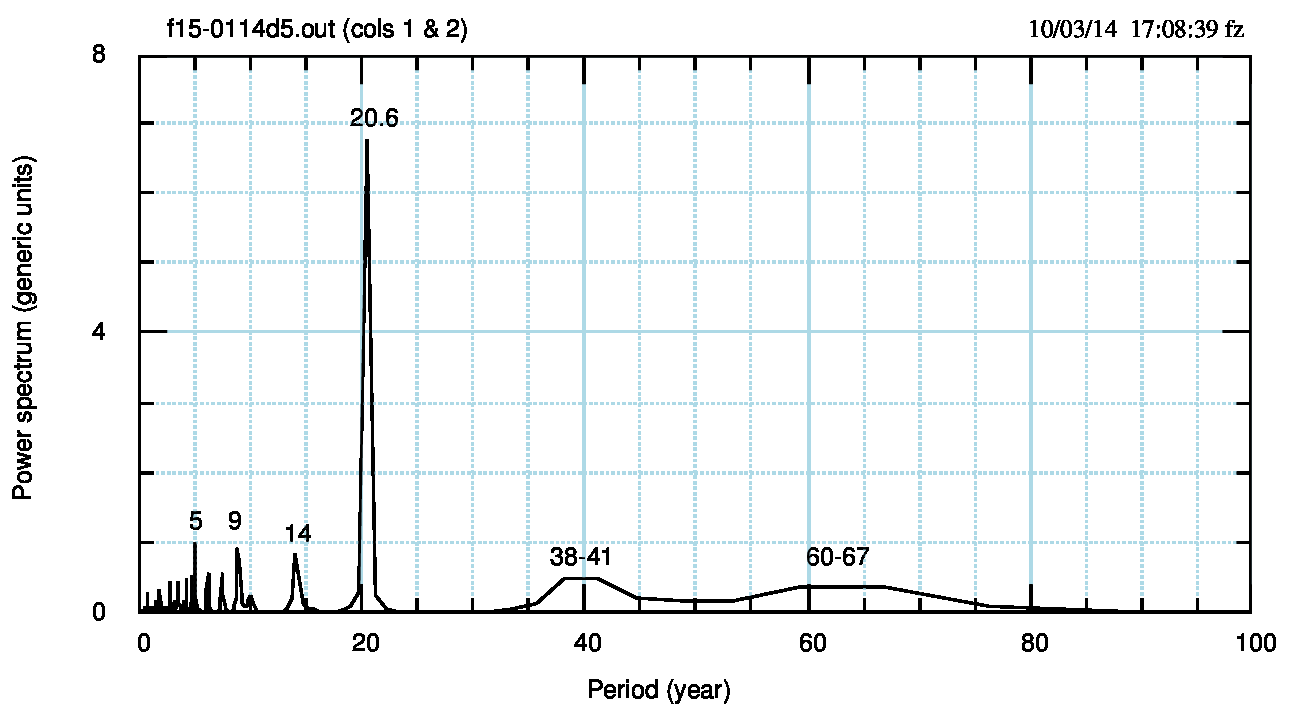
Qui bisogna mettere in evidenza che:

1. il periodo di 67 anni è stato in gran parte “catturato” dalle funzioni usate e diventa un plateau di 60-67 anni con potenza circa 15 volte inferiore rispetto a quella dei dati originali;
2. è emerso un periodo, a cavallo dei 40 anni, non visibile nello spettro dei dati osservati;
3. il periodo di 5 anni mantiene la sua marginalità ma anche la sua esistenza, già evidenziata nei lavori di N. Scafetta sui periodi planetari;
4. il periodo di 20 anni diventa il più importante anche se la potenza diminuisce di circa il 17% rispetto ai dati senza detrending.

Tutto questo mostra come il detrending e l’analisi dei dati che da esso derivano richieda attenzione e strumenti adeguati.

NB: Il discorso prosegue con il post di domani con una analisi dei dati dell’articolo Moffa et al., che abbiamo discusso la settimana scorsa.