Dopo il post sul massimo a 2.87 anni, che trovate qui, ho pensato che sarebbe stato più corretto rendere quel massimo indipendente dal singolo dataset e usarlo per confrontare tra loro le diverse variabili climatiche. Anche se in genere i massimi spettrali si normalizzano rispetto al massimo assoluto dello spettro, nel caso della Massima Entropia non mi è sembrato di doverlo fare a causa dei picchi che vengono generati alle alte frequenze, in particolare usando un numero di poli alto, pari alla metà dei dati.
Ho preferito quindi normalizzare rispetto alla somma delle potenze, così, per tutti i 25 dataset di cui dispongo ho calcolato il rapporto tra la potenza e la potenza totale, in particolare registrando questo rapporto per il massimo di 2.87 anni (in realtà ho utilizzato i periodi compresi tra 2.84 e 2.91 anni, con un intervallo di poco superiore all’1% rispetto al valore nominale di 2.87). La potenza normalizzata copre un intervallo di circa 3 ordini di grandezza, da 10-5 a 10-2. Ho poi ordinato in senso crescente le potenze, associando ad ognuna un numero d’ordine (1 per la potenza minima, 25 per quella massima). Il risultato è riassunto nella tabella successiva:
Table I
2.87 yrs Ordered Normalized Power
| N | DataSet | Period | Power | Notes |
|---|---|---|---|---|
| 1 | amo-yea-int.dat | 2.8770001 | 1.70214735E-05 | Yes |
| 2 | amo-warm-int.dat | 2.8910000 | 1.92137832E-05 | Yes |
| 3 | cr-int.dat | 2.8850002 | 2.51082220E-05 | No |
| 4 | amo-cold-int.dat | 2.8630002 | 3.29684481E-05 | Yes |
| 5 | tsi-int.dat | 2.8920002 | 4.16001567E-05 | Yes? |
| 6 | pdo-int.dat | 2.8830001 | 6.31855874E-05 | Yes |
| 7 | aa-int.dat | 2.8730001 | 7.31600521E-05 | No |
| 8 | ss-int.dat | 2.9090002 | 1.13695576E-04 | No |
| 9 | ssn1212-int.dat | 2.9090002 | 1.76671922E-04 | No |
| 10 | nao-cold-int.dat | 2.8840001 | 2.30689402E-04 | No |
| 11 | nl-int.dat | 2.8740001 | 2.95852456E-04 | Yes |
| 12 | nao-yea-int.dat | 2.8840001 | 3.91922949E-04 | No |
| 13 | num-yea-int.dat | 2.8750002 | 5.29294659E-04 | No |
| 14 | 1112-nino-int.dat | 2.8740001 | 6.90981746E-04 | Yes |
| 15 | nam-int.dat | 2.8840001 | 7.62321346E-04 | Yes |
| 16 | ssthc-int.dat | 2.8690002 | 8.17735330E-04 | Yes |
| 17 | hc3-int.dat | 2.8810000 | 8.27233482E-04 | Yes |
| 18 | sst-int.dat | 2.8620002 | 1.16371899E-03 | Yes |
| 19 | 1212-int.dat | 2.8760002 | 2.13416340E-03 | Yes |
| 20 | maiana-int.dat | 2.8380001 | 3.06738121E-03 | Yes? |
| 21 | nao-warm-int.dat | 2.8840001 | 6.80405833E-03 | No |
| 22 | nao1-int.dat | 2.8950002 | 1.38859032E-02 | Yes |
| 23 | 1112-int.dat | 2.8740001 | 1.64635703E-02 | Yes |
| 24 | soi-int.dat | 2.9130001 | 1.85544807E-02 | Yes |
| 25 | mei-ext-int.dat | 2.8720002 | 4.29179780E-02 | Yes |
Nella tabella ho mantenuto l’indicazione della presenza o meno del picco a 2.87 anni, ma non era necessario farlo: indipendentemente dall’eventuale massimo, ho registrato il valore della potenza corrispondente al periodo di 2.87 anni. Se nell’intervallo, descritto sopra, di circa l’1%, era presente un massimo, veniva registrata la potenza di quel massimo. La cosa che conta qui è il valore della potenza, non l’esistenza o meno di un massimo.
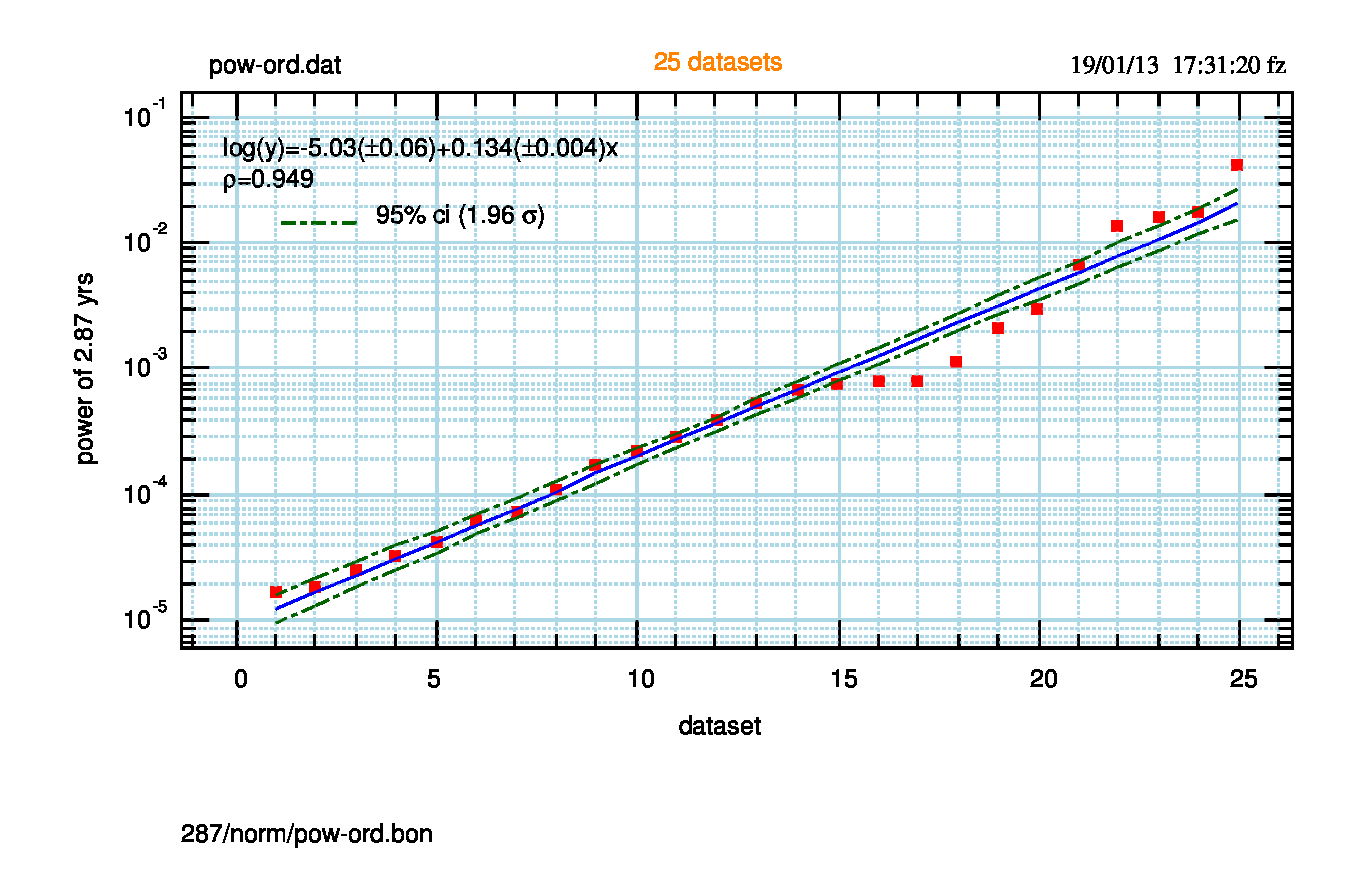
La Fig.1 mostra il grafico e il fit del logaritmo della potenza rispetto al numero d’ordine dei dataset (lo stesso grafico accoppiato ad una funzione di smoothing a 5 punti che sottolinea le oscillazioni).
Quali informazioni si possono trarre da questo grafico? Intanto che esiste una relazione lineare netta tra logaritmo della potenza a 2.87 anni e dataset, nel senso che c’è un’evoluzione nel contenuto dei dataset al crescere della potenza. E questo è messo in evidenza sia dalla bassa incertezza sui parametri del fit (1% e 3% rispettivamente) che dal coefficiente di correlazione pari a 0.95.
Quale sia l’evoluzione del contenuto dei dataset è più difficile saperlo in modo quantitativo: si può valutare il “contenuto di oceano” e il “contenuto di Sole” dei singoli dataset – come all’incirca ho fatto nel post precedente – e notare che le potenze spettrali maggiori hanno relazione con NAO (dal 1826 al 2000), GHCN di novembre 2012, SOI, MEI ma, anche, con GHCN di dicembre 2012, SST di NOAA, HadCrut3, SST di Hadley Center. E che le minori potenze sono legate ad AMO (nelle forme di media annuale, media sul semi-anno caldo e sul semi-anno freddo), al modello di Usoskin dei raggi cosmici, all’irraggiamento totale del Sole (TSI), all’indice geomagnetico aa, al numero di macchie solari (per la descrizione dei singoli dataset sarebbe bene avere sott’occhio la tabella del post precedente qui, ricordando che i dataset aggiunti sono le medie caldo-freddo di AMO e NAO e GHCN di dicembre 2012). Come al solito, tutti i dati relativi a questo post sono disponibili al sito di supporto.
Si potrebbe anche tentare di valutare l’influenza del Sole sui dataset (che, ricordo, c’è sempre anche se può essere più o meno forte, più o meno nascosta e mediata da feedback di vario genere) usando un metodo come quello descritto da Berger (2008) per giustificare il forte massimo di 7.74 anni nello spettro della NAO. Berger usa l’equazione della differenza di toni (equation for difference tones) y=a·b/(a-b) – con a,b periodi da combinare e a>b – e ricava 7.74 anni combinando un ciclo solare di 10.33 anni e il periodo del perigeo lunare di 4.425 anni. Ho provato a combinare il massimo a 7.86 anni presente nei miei dati NAO con il massimo, oggetto di questo post, a 2.89 anni e trovo un massimo risultante di 4.57 anni che non so bene a quale periodo solare riferire (forse a 1/4 – 4.65 anni – del periodo dei nodi lunari, di 18.6 anni), anche se è in buon accordo con il massimo a 4.494 anni, ben visibile sullo spettro.
Questo metodo, applicato a 25 dataset, diventa pieno di incertezze e arbitrarietà e va ben al di là dello scopo del post che è, al più, quello di gettare un sassolino nello stagno.
Ancora, nessuno dubita dell’influenza solare sugli anelli degli alberi, ma nella descrizione del lavoro pioneristico di A.E. Douglass, Berger (2010) mette in evidenza come in alcuni casi (slide 11 ad esempio) l’influenza solare, ammesso che ci sia, è di importanza secondaria.
[line style=”normal”] prova shortcodes [/line]
Bibliografia
- W.H. Berger: Solar modulation of the North Atlantic Oscillation: Assisted by the tides?, Quaternary International 188, 24-30, (2008)
- W.H. Berger: A.E. Douglass (1867-1962) and solar cycles in tree rings, 2010. Liberamente scaricabile da qui

[…] sul picco di circa 2.87 anni si trovano su CM (qui e qui). Questo picco ha un andamento di potenza/periodo simile al picco di 21-22 anni. Dal grafico si […]