Ricostruiamo l’Hockey Stick con R

Ultimamente ci siamo occupati di analizzare le temperature e la CO2 tramite il programma open source R. Presto pubblicheremo altre analisi e metodi statistici più raffinati. In attesa di questi nuovi tutorial, diversamente dal solito, oggi analizzeremo il programma scritto da Jeff Id che cerca di replicare il sistema utilizzato per creare l’hockey stick.

Prima di procedere, ricordo che R è disponibile sia per Microsoft Windows che per Linux.

La domanda che molti si staranno ponendo è: perchè tornare di nuovo sull’Hockey stick? La risposta non è univoca e possiamo dire che principalmente si torna sull’argomento in quanto l’ultima versione dell’HS è stata edita nel 2008 e poi perchè è sempre una notevole fonte di riflessione sulla ricerca scientifica. In questo articolo, però, affronteremo il “semplice” aspetto scientifico.

Secondo l’autore del programma1 (scritto in R) che andremo ad analizzare, quello che è successo con l’HS è molto semplice: dal set iniziale di proxy sono stati eliminati quelli che mostravano una correlazione debole con le temperature. La correlazione viene calcolata tra gli anni più recenti dei proxy e quelli più recenti delle temperature. Questa operazione preliminare ha fatto sì che Mann scartasse, dal set iniziale di 1209, ben 725 proxy che non rispondevano al criterio imposto di correlazione. Su questo fatto torneremo più avanti, perchè abbiamo visto di recente come i proxy siano spesso impossibili da legare in alcun modo alle temperature.

La fase successiva prevede di calibrare la deviazione standard dei proxy selezionati al punto precedente, in modo tale che questa coincida con la deviazione standard del segnale di controllo. In questo modo i proxy selezionati avranno delle oscillazioni che coincideranno molto bene con le oscillazioni delle temperature.

Infine calcoliamo la media del set di proxy selezionati e fin qui elaborati.

Stiamo per verificare, tramite questo programma in R, come il succitato metodo consenta di calibrare i set di proxy in modo tale che il segnale di controllo emerga sempre e comunque. Qualsiasi segnale di controllo si stia cercando. Questo è il punto focale di tutta la ricerca, ovvero il metodo CPS (Composite Plus Scale) che è stato inventato ad hoc per gestire un elevato numero di dati proxy e per ricreare un qualsiasi segnale di controllo. L’autore del programma intravvede malafede in questo metodo, noi semplicemente sottolineiamo come spesso in climatologia, non paghi dei metodi statistici correnti, ci si avventuri nell’invenzione di qualche nuovo filtro o metodo di regressione.

Un avvertimento per i gentili lettori: stiamo per iniziare una trattazione piuttosto lunga e corposa, il consiglio è di scaricare lo script e di tenere la vostra versione di R aperta e a portata di mouse.

Introduciamo l’argomento con un semplice esempio, anche per chi non mastica troppo di statistica. Per fare ciò utilizzeremo uno strumento che oggi sempre più persone hanno sul proprio computer di casa: un elaboratore di immagini. La tecnologia oggi è molto raffinata e ci consente di mettere sempre più spesso una “toppa” a fotografie scattate male o distrattamente. Ipotizziamo di fotografare una nuvola e di sovraesporla (un classico): vogliamo il cielo blu intenso e purtroppo la nuvola si brucia completamente. Ebbene, gli editor digitali di fotografie ci consentono di rimediare al nostro errore, andando a correggere il contrasto complessivo della foto. Se siamo fortunati, la sovraesposizione ha lasciato qualche dettaglio (in termini digitali, abbiamo ancora delle informazioni da poter elaborare). Niente di meglio per il programma che va a caccia di quelle poche informazioni presenti e riesce a restituirci i dettagli della nuvola. Se siamo stati sfortunati (o di mano troppo pesante), all’interno della nuvola avremo pochissime o nessuna informazione e, a quel punto, nessuno programma potrà mettere in luce alcun dettaglio.

Tutto questo preambolo per dire cosa? Uno dei pilastri fondanti dell’indagine statistica è la presenza di dati. Se abbiamo un campione numeroso, ci possiamo lavorare tranquillamente. Se, diversamente, non abbiamo un campione numeroso, anzi addirittura abbiamo scarsità di dati, non c’è algoritmo che tenga: non possiamo ricostruire qualcosa da una serie rarefatta. Mutatis mutandis, da una serie rarefatta possiamo tirare fuori qualsiasi cosa.

Ecco cosa succede con il metodo statistico sopra descritto: dai proxy così selezionati e scalati, in realtà possiamo ottenere qualsiasi tipo di segnale, semplicemente andando a cambiare il segnale di controllo. Volete temperature in aumento a fine millennio? Nessun problema. Volete temperature (sempre con gli stessi proxy) in diminuzione a fine millennio? Neanche questo è un problema. Infine, volete temperature che oscillano a fine millennio? Nemmeno a dirlo, si può fare anche questo.

Il listato originale lo potete trovare a questo link, per una migliore comprensione, tuttavia, lo analizzeremo nei suoi punti più interessanti.

Inizializziamo lo script e carichiamo i dati. Se caricate lo script con una connessione internet attiva, il programma scaricherà automaticamente tutto quanto necessario per eseguire i calcoli (diversamente dovrete scaricarvi i dataset manualmente e andare a modificare il percorso sul vostro disco rigido). Ricordo che lo script è stato elaborato da Jeff Id.

###########################################################################
##################### TURNKEY DATA DOWNLOADER #############################
###########################################################################
method=”online”
if (method==”offline”) {load(”d:/climate/data/mann08/mann.tab”)
load(”d:/climate/data/mann08/mannorig.tab”)
load(”d:/climate/data/mann08/idorig.tab”)
names(mannorig)=idorig$idorig
load(”d:/climate/data/mann08/details.tab”)
source(”d:/climate/scripts/mann.2008/instrumental.txt”)} else {
url=”http://www.climateaudit.org/data/mann.2008″
download.file(file.path(url,”mann.tab”),”temp.dat”,mode=”wb”);load(”temp.dat”)
download.file(file.path(url,”mannorig.tab”),”temp.dat”,mode=”wb”);load(”temp.dat”)
download.file(file.path(url,”details.tab”),”temp.dat”,mode=”wb”);load(”temp.dat”)
download.file(file.path(url,”idorig.tab”),”temp.dat”,mode=”wb”);load(”temp.dat”)
names(mannorig)=idorig$idorig
source(”http://www.climateaudit.org/scripts/mann.2008/instrumental.txt”)}

Nulla da dire fin qui, carichiamo una serie di dataset ospitati sul sito Climate Audit, in buona sostanza è l’insieme dei proxy necessari per l’analisi.

############################################################################
################ FUNCTIONS ################################################
############################################################################

######## CREATE TIME SERIES ##########
gg = function(X)
{
ts(X[,2],start=X[1,1])
}

######## GAUSSIAN FILTER FUNCTION TESTED AT CA #########
######## set to 11 years ###############################
source(”http://www.climateaudit.org/scripts/utilities.txt”)

ff=function(x)
{
filter.combine.pad(x,truncated.gauss.weights(11) )[,2]
}
##########################
##### END FUNCTIONS ######
##########################

Con questo secondo blocco creiamo una serie di funzioni che ci torneranno utili nel corso dell’elaborazione. La prima funzione “gg” imposta lo schema base per creare le serie storiche (il comando ts è già stato analizzato a fondo su Climate Monitor, vi invito a dare un’occhiata ai tutorial pubblicati). La funzione “ff”, invece, si occupa di filtrare le serie storiche. Il filtro applicato è un gaussiano centrato su periodo di tempo di 11 anni2 .

mano=mannorig #copy non-infilled PROXY series to different memory
#mano=mann #copy REGEM infilled PROXY series to different memory

In questo blocco abbiamo la prima scelta possibile. La variabile “mano” è di default settata per caricare i proxy “mannorig” (serie non completata tramite il metodo RegEM), tuttavia è possibile scegliere la serie “mann” che al contrario è completata con il sistema RegEM. Per fare questo basta deselezionare la riga “mannorig” con il simbolo # ed eliminandolo dalla riga “mann”.

for(i in 1:lent)
{
mano[[i]][,2]=ff(mano[[i]][,2])
}

Il blocco precedente è molto interessante, in quanto ci consente di filtrare ricorsivamente tutti i proxy con la funzione “ff” che abbiamo incontrato precedentemente. E’ un normale ciclo “for” utilizzato in modo sapiente all’interno di R.

#m=c(1:leng)/-leng ###### 0 to -1 NEGATIVE linear slope
#m=c(1:leng)/leng ###### 0 to 1 POSITIVE linear slope
#m=sin( (1:leng)/(leng/cycles)*pi) #sin wave with # cycles
m=-sin( (1:leng)/(leng/cycles)*pi) #-sin wave with # cycles

Questa sezione è molto importante perchè troviamo le funzioni che riproducono il segnale di controllo. Ne abbiamo di diverso tipo: temperature crescenti, decrescenti e oscillanti. Anche in questa sezione possiamo operare una scelta (l’invito è provarle tutte per vedere come le serie proxy si adattano perfettamente a ogni tipo di segnale).

Jeff Id opera una serie di calcoli preparatori che qui tralasceremo, per passare direttamente al cuore di tutto il programma: il Composite Plus Scale (CPS).

for(j in 1:lent)
{
if(pass[j]==TRUE)
{
y=(gg(mano[[j]]))
val = window(y, start(m)[1],end=end(m)[1])
m0=mean(val,na.rm=T)
sd0=sd(val,na.rm=T)

################# CPS METHOD IS APPLIED HERE #######################

yscale=y-m0
yscale=yscale/sd0
yscale=yscale*ssig
yscale=yscale+msig

x=ts.union(x,ts (yscale,time(y)[1]))
}
}

In questo ciclo “for” molto importante, innanzitutto scremiamo i proxy, scartando quelli che non rientrano nella correlazione desiderata con le temperature, quindi le serie vengono troncate negli anni in cui esistono i dati del segnale di controllo. L’abbiamo detto sopra, vengono utilizzati gli ultimi anni disponibili nei proxy e gli ultimi anni disponibili nel segnale di controllo delle temperature. Le operazioni di centratura e scalatura vengono effettuate solo sulla base di questo periodo.

Calcoliamo quindi la media m0 e la deviazione standard sd0. Adesso siamo pronti per il CPS: sommiamo tutti i proxy, non prima di averli centrati su m0 e scalati con sd0. In particolare per la deviazione standard, essendo a denominatore:

yscale=yscale/sd0

al crescere della deviazione standard (quindi dell’oscillazione complessiva del proxy), cresce la scalatura del proxy derivato. Questo è importante: abbiamo eliminato i proxy che non coincidono con la correlazione da noi cercata, e ora scaliamo in modo più deciso quei proxy che oscillano di più (al di fuori del periodo di calibrazione, non dimentichiamolo!).

Infine i proxy vengono sommati ricorsivamente e assemblati per avere un unico proxy del quale viene poi calcolata la media. Questo è il valore che viene rappresentato nei grafici.

Ricostruzione delle temperature tramite segnale di controllo crescente.

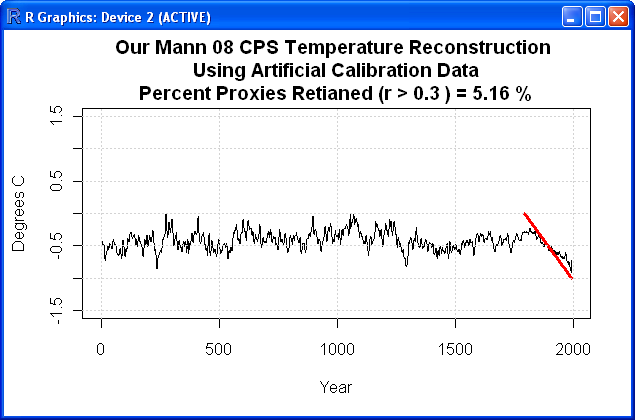
Ricostruzione delle temperature tramite segnale di controllo decrescente.

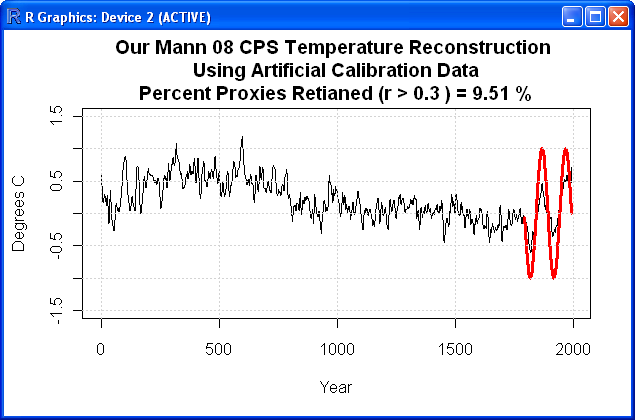
Ricostruzione delle temperature tramite segnale di controllo oscillante.

1. http://noconsensus.wordpress.com/2009/06/20/hockey-stick-cps-revisited-part-1/ [↩]
2. Un approfondimento molto tecnico http://www.ltrr.arizona.edu/~dmeko/notes_8.pdf [↩]